- Payoff: the gross outcome of an investment or trade. The amount you earned from that trade, regardless of commissions, extraneous costs, etc.
- Profits: the gross outcome of an investment or trade, including commissions, extraneous cost
- → the distinction happens in Options (Finance). Payoffs don’t consider the option premium, while the profits do.
- Return: short for “rate of return”. The percentage of profit (not payoff!) per original investment. Quoted in percentage (%) or log-returns. def. No arbitrage condition (=Law of One Price means without any risk, there cannot be excess return (=return above risk-free rate).
- let security have payoff , cost and payoff , cost .
- If then Alternative formulation:
- If security is risk-free and has payoff …
- …then the current price of should simply be the DCF of discounted at the risk-free rate
Risk-Neutral Assumption
Motivation. People in general are risk-averse. Observe in the following example1: Consider:
- A bond with principal \160%$ of the principal
- A put option that acts as insurance on this bond, that pays nothing if solvent, and if default.
- Your portfolio contains both. Assume for simplicity risk-free rate .
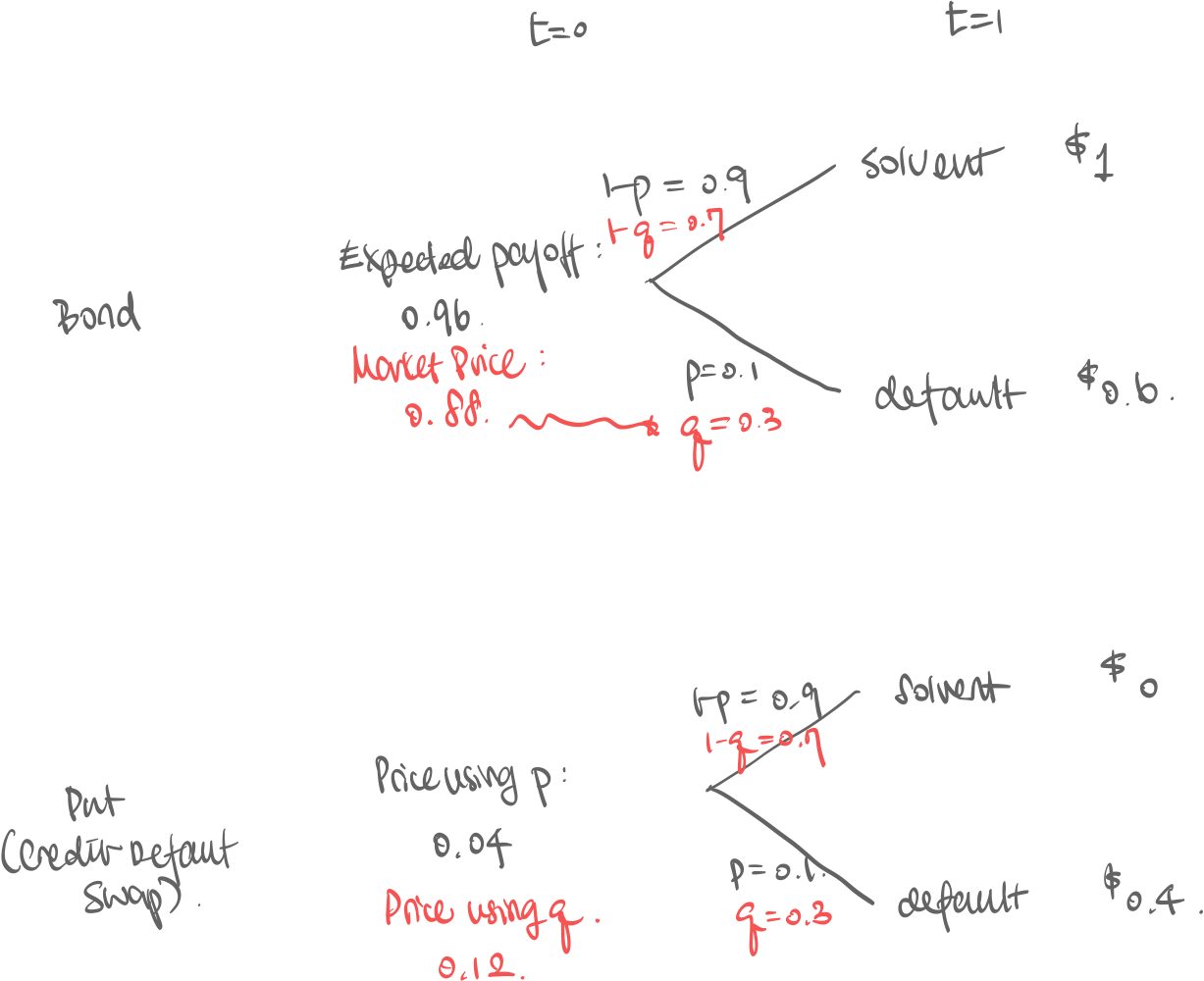 Our objective is to price the put option so that the law of one price applies. The naive approach:
is the historical default rate from data.
Our objective is to price the put option so that the law of one price applies. The naive approach:
is the historical default rate from data. - The expected payoff of bond calculated from is
- The expected value of put calculated from is
- Total payoff of portfolio is always \1$ regardless of solvency
- And both sum up to \1$ which is same as total payoff, thus LoP applies
- ! …but this is NOT the observed market price of bond: \0.88$! The investors are demanding a risk-premium (=acting irrational) because they’re risk-averse So we try a different method:
- From the market price \0.880.88=(1-q)\cdot1+q\cdot 0.6q=0.3$
- Calculate the put option from this to get price \0.12$
- And both sum up to $1 which is same as total payoff thus LoP applies
- 0.88.
def. Risk-Neutral Assumption. A method of pricing derivatives despite the fact that investors are acting irrationally, that makes arbitrage impossible (=makes law of one price hold.)