SQL Query Processing Algorithms

Notation §

• $B(R)$: block count of table $R$
• $|R|$: tuple count of table $R$
  • $|R|>>B(R)$ because many tuples fit in a block
• $M$: number of available blocks in memory
• Complexity is always the number of I/Os

Sorting Based Algorithms §

alg. External Merge Sort

• Idea: Merge Sort, but with limited memory

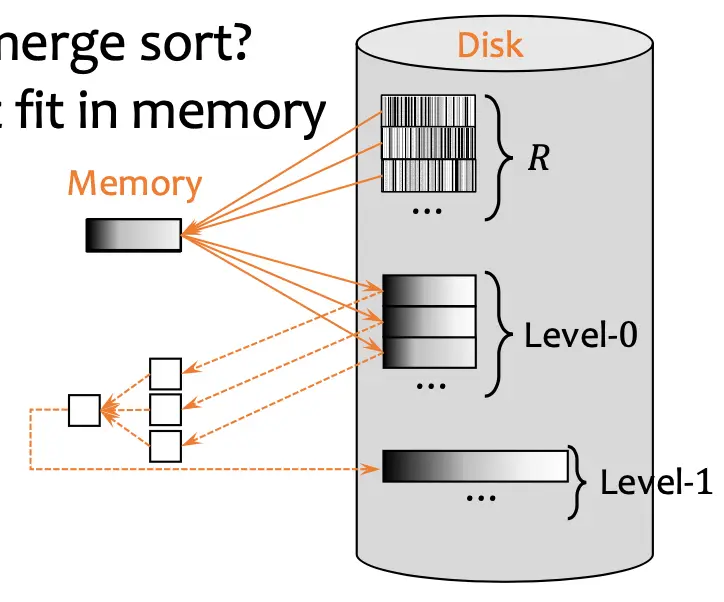
1. We are trying to sort relation $R$ on disk with $M$ blocks of main memory
2. Pass 0: we read $M$ sequential blocks at a time, sort (using any Sorting Algorithms) and read onto disk into different runs. The number of runs is $n$.
3. Pass 1: We merge teach runs in memory. We need one block to write out the result, and $n$ blocks to merge simultaneously.
   1. Thus $n=M-1$
4. Repeat passes until there is only one output run. This is the sorted run.

• Complexity
  • Number of passes: $=\lceil {\log }_{M-1}\lceil \frac{B(R)}{M}\rceil \rceil +1$
  • I/O Complexity: $\approx O(B(R){\log }_{M}B(R))$
  • Memory requirement: $M$ (as much as possible)

alg. Sort-Merge Join Idea: while sorting the table, simultaneously join them in the process: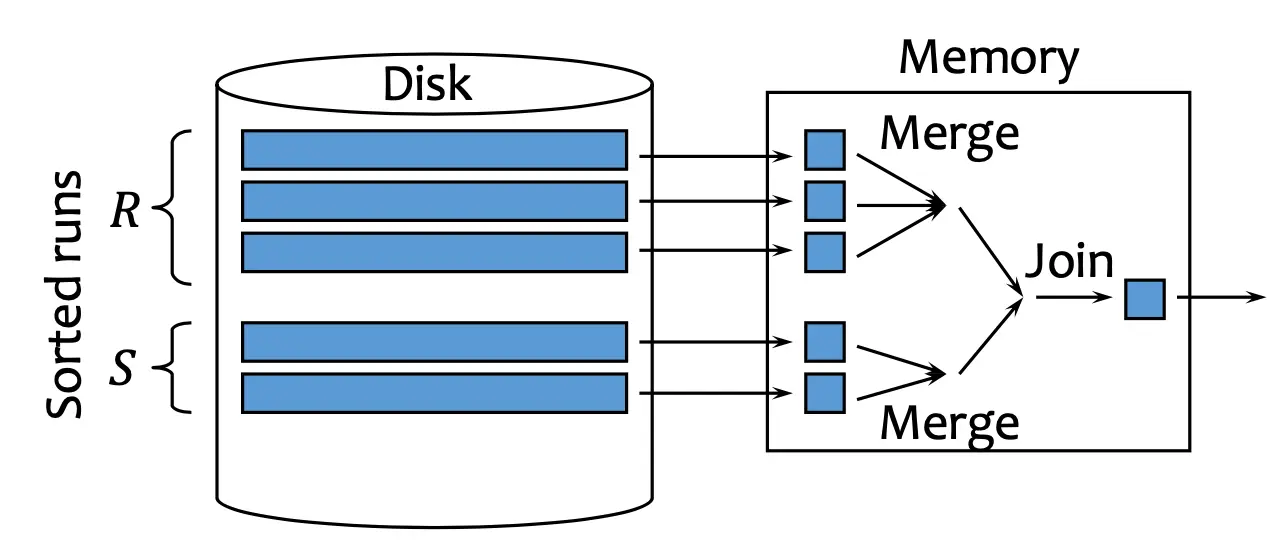

1. Run external merge sort passes until the no. of total runs to merge is less than or equal to $M-1$
2. Merge each table in-memory, and compare them to the condition. Join if necessary.

• Complexity for 2 passes:
  • IO Complexity in 2 passes: $O(B(R)+B(S))$
  • Memory requirement: $M>\lceil \frac{B(R)}{M}\rceil +\lceil \frac{B(S)}{M}\rceil =\sqrt{B(R)+B(S)}$
• Complexity for $>2$ passes: same as external merge sort
• ! May degrade complexity if, e.g. the whole table needs joining.

Hash Based Algorithms §

alg. Hash Join

• Idea: use a $O(1)$ hash function that partitions the table into block size $M-1$ partitions, then merge:

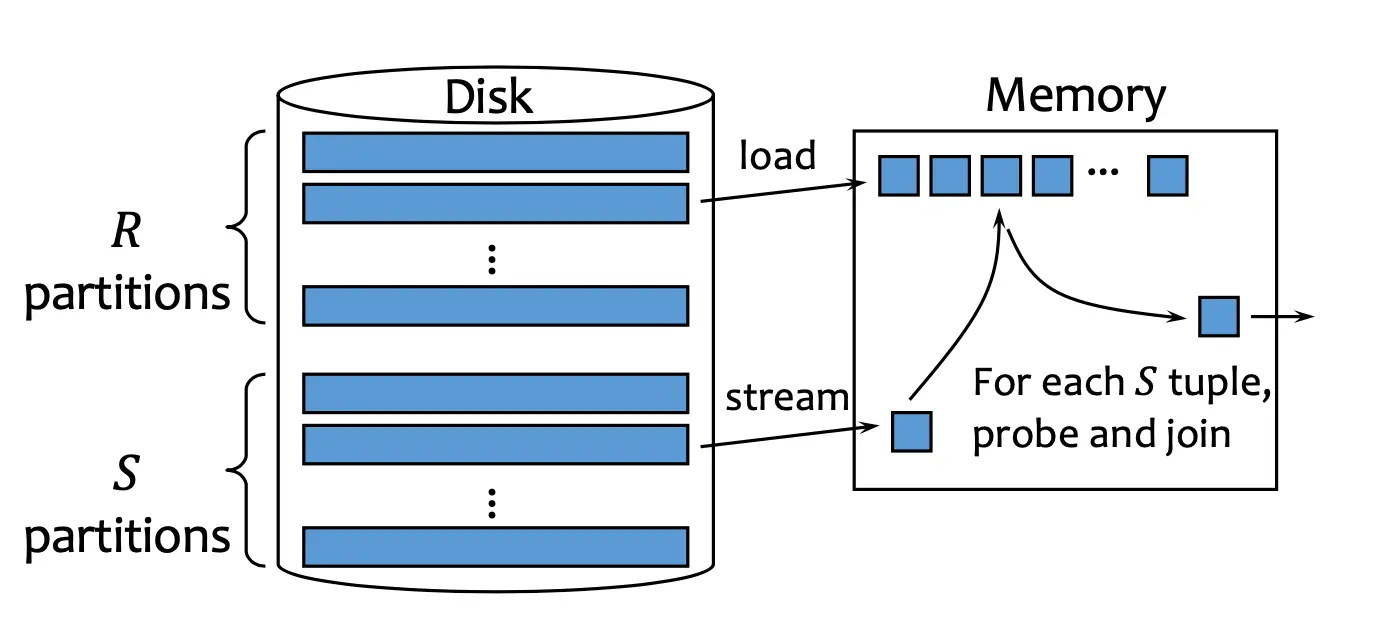
1. Probe: Partition both tables $R,S$ into block size $M-1$ different partitions using the same hash function
2. Load one partition of $R$ into memory. Stream one block of $S$ at a time, and join.

• Complexity
  • I/O: $3(B(R)+B(S))$
  • Memory requirement: $M>\sqrt{min[B(R),B(S)]}+1$

Index Based Algorithms §

Equality and Range: use B+ Trees

Index Nested Loop Join

Zigzag Join