Motivation. Let’s say that there is a relationship between GDP per capita and life expectancy. Maybe god has declared a perfect formula describing this relationship:
\text{GDP Per Capita}=200\cdot \text{Life Expectancy}+1000+\text{Noise} $$While we humans may never truly know the parameters of the formula, $200$ and $1000$, we can still make a good guess about it. Therefore, assuming this is a linear relationship, we have the Bivariate Ordinary Least Squares Model.Y_{i}=\beta_{0}+\beta_{1}X_{i}+\epsilon_{i}
where $(X_{1},Y_{1}),\dots,(X_{n},Y_{n})$ are observations (=regressors). thm. **Parameter OLS Estimator** for $N$ observations $(X_{i},Y_{i})$:\begin{align} \hat{\beta_{1}}&\coloneqq \frac{\sum_{i=1}^n(X_{i}-\bar{X})(Y_{i}-\bar{Y})}{\sum_{i=1}^nX_{i}-\bar{X}} \ \hat{\beta_{0}}&\coloneqq \bar{Y} - \hat{\beta_{1}}\bar{X} \ \end{align}
**Properties.** - Predictor: $\hat{Y_{i}}=\hat{\beta_{0}}+\hat{\beta_{1}}X_{i}$ - Residual: $\hat{\epsilon}\coloneqq Y_{i}-\hat{Y}$ is the estimator for the error term, i.e. how good the predictor is. - *Regression Variance*: $\hat{\sigma}^2=\frac{\sum_{i=1}^N\hat{\epsilon_{i}}^2}{N-k}=\frac{\sum_{i=1}^N(Y_{i}-\bar{Y})^2}{N-k}$ where $k$ is the number of parameters ($k=2$ in this case) - basically the [[Mean Squared Error]]. The lower the better. - This is also the *standard error of the residuals*. - In *Stata*, it's called the `Root MSE`. **Evaluation of Estimators.** - Mean of $\hat{\beta_{1}}$: $\mathbb{E}(\hat{\beta_{1}})=\beta_{1}+\rho_{X,\epsilon}\frac{\sigma_{\epsilon}}{\sigma_{X}}$ - Thus *bias* is $\rho_{X,\epsilon}\frac{\sigma_{\epsilon}}{\sigma_{X}}$ - If $\rho_{X,\epsilon}=0$ then exogenous (good!) - If $\rho_{X,\epsilon}>0$ then there's some 3rd factor positively correlated with $X$, thus bias is positive. - If $\rho_{X,\epsilon}<0$ then v.v. - & Thus the bias characterizes exogeniety - Variance of $\hat{\beta_{1}}$: $\text{Var}(\hat{\beta_{1}})=\frac{\hat{\sigma}^2}{N\cdot \text{Var}(x_{i})}$ - This is also called *precision* - $\sqrt{ \text{Var}(\hat{\beta_{1}}) }$ is also called *standard error* of $\hat{\beta_{1}}$. - ! For random variables, $\sqrt{ \text{Var}(X) }$ is called standard deviation. For estimator random variables, it is called standard error. An abuse of terminology. ## Confidence Intervals and Hypothesis Testing See also: [[Confidence Intervals]] and [[Hypothesis Testing]] **Motivation.** Assume we have our estimators for our sample size $N$ using OLS, $\hat{\beta_{0},\hat{\beta_{1}}}$. Now, assuming we have the true population data (impossible in real life) and take $100$ samples of size $N$ from the whole population, we get $100$ different tuple of estimators $(\hat{\beta_{0}},\hat{\beta_{1}})$. If we plot these on a graph, we get an approximate bell curve. This is due to the [[Central Limit Theorem]]. Knowing this fact, we can deduce if there is a correlation between $X$ and $Y$. 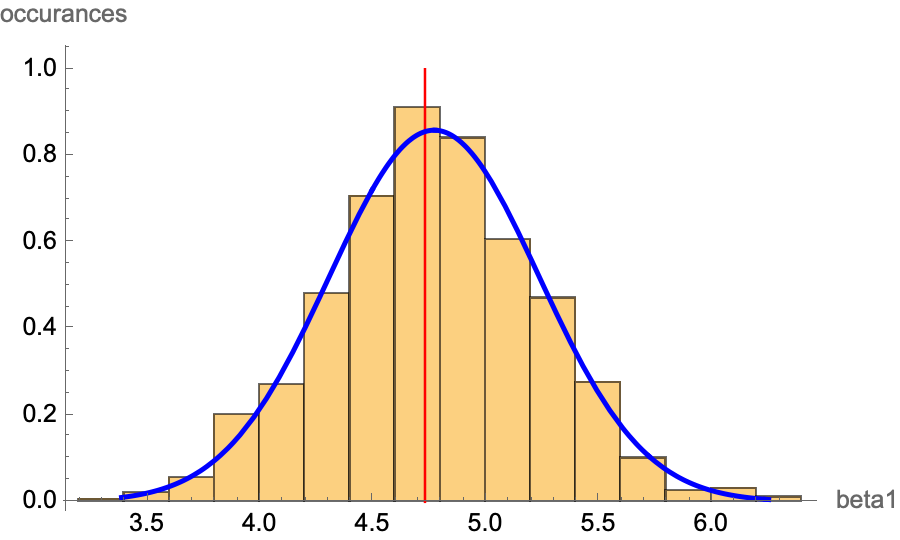![[Ordinary Least Squares Regression-20240213172422991.png|416]] **Remark.** $N\geq 30$ is the minimum required for CLT. $N\geq 100$ is a conservative requirement for CLT to apply. **Remark**. We will only look at $\hat{\beta_{1}}$ since it is the more important parameter. ### Hypothesis Testing def. The **Null hypothesis** in regression is $H_{0}:\beta_{1}=0$, i.e. there is no correlation. def. **Regression T-test.** See [[Student's t-test]]. A T-test is a test for rejecting the null hypothesis. let the T-statistic $T=|\frac{\hat{\beta_{1}}-\beta_{1}^\text{Null}}{\sqrt{ \text{Var}(\hat{\beta_{1}}) }}|$. Then\begin{cases} H_{0} & \text{if } T>K \ H_{1} & \text{otherwise} \end{cases}
- The cutoff value $K$ is determined by how powerful (=$\alpha$) you want the test to be. This is determined by the [[Student's T-Distribution]]. - This is because $T=_{d}t_{N-1}$ - This is [[Student's t-test]] but with only one random variable. - Normally, we set the cutoff $K=2$, i.e. two standard deviations away. This is around an $\alpha=0.05$ test. ### Confidence Interval Intuition. Bias: standard error of regression: mean squared of residuals; also the estimator for the error Standard error of... - Residuals → standard error of regression - $be$ Varaince of $\hat{\beta_{1}}$ is also the variance of CLT limit with the *same sample size* ## Omitted Variables