Compensating and Equivalent Variation

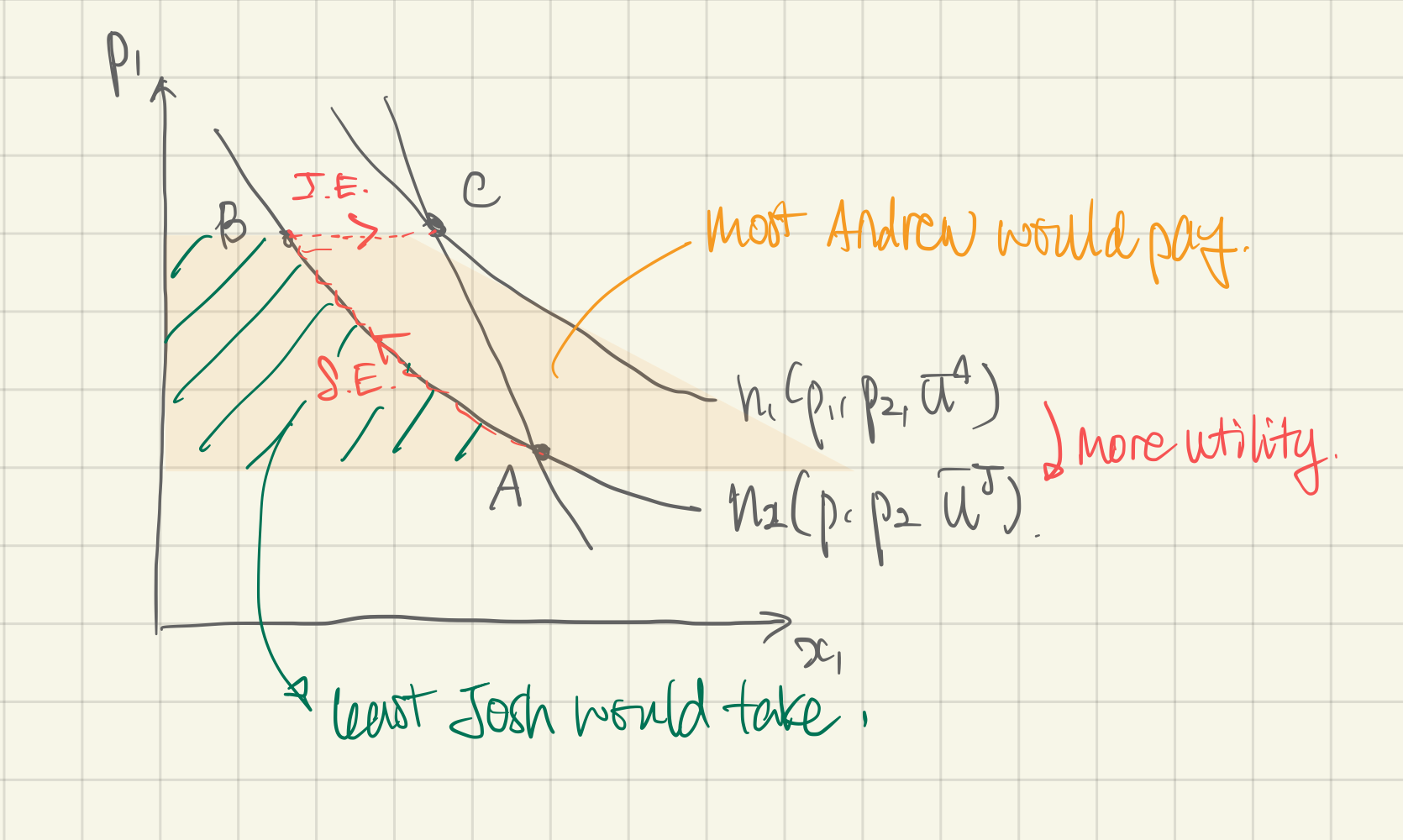
Q. Coupon Exchange Problem. Josh and Andrew have identical utility functions $u(x_1,x_2)$ where $x_1$ is milkshakes and $x_2$ is toys.

• Their incomes are the same
• Josh has a 50% off coupon for $x_1$.
• ⇒ Can Josh and Andrew work out a trade where Andrew buys the coupon? Figure out
• Least Josh would take for the coupon using the expenditure function
• Most Andrew would pay for the coupon (also using the expenditure function)
• ⇒ Trade occurs when (least Josh would sell for) < (most Andrew would pay for)

Idea

CV and EV - YouTube Oh no! the price of good $x_1$ increased!

• 🥺 She’s now at a lower Indifference Curve. How much should we give as compensation to get her back on the original indifference curve? ⇒ Compensating Variation
• 😈 She’s at a lower inx_{1}$ increase, we just take money away from her directly? ⇒ Equivalent Variation

def. Compensating Variation (CV). When a price of a good changes, the Compensating variation is the change in expenditure ($\pm$) required to maintain the utility.

def. Equivalent Variation (EV). An individual may trade a change in income ($\pm$) for a change in prices.

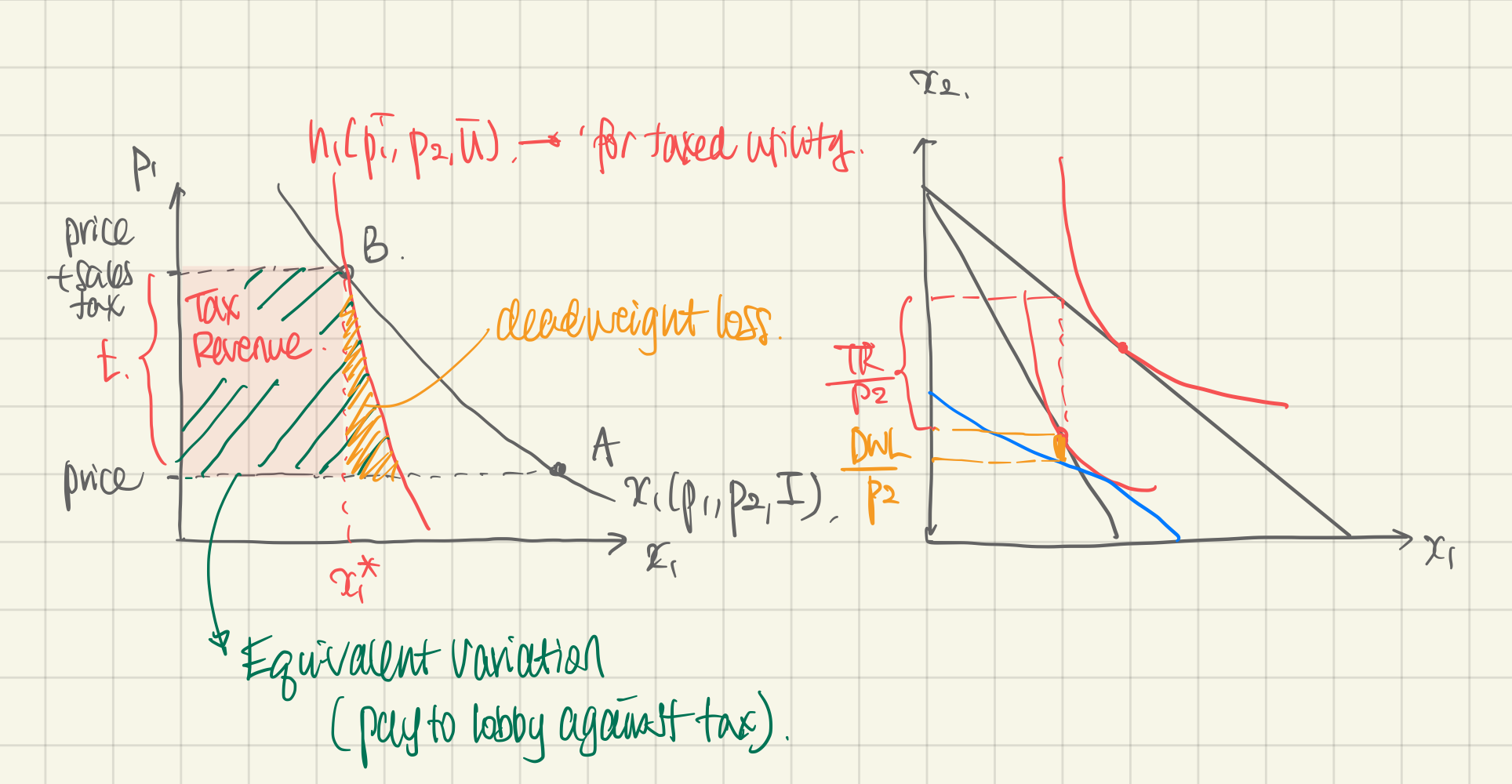
Compensating Variation (CV) is how much money an individual would have to get (or have taken away) to be indifferent to the change in prices