Equilibria in Game Theory

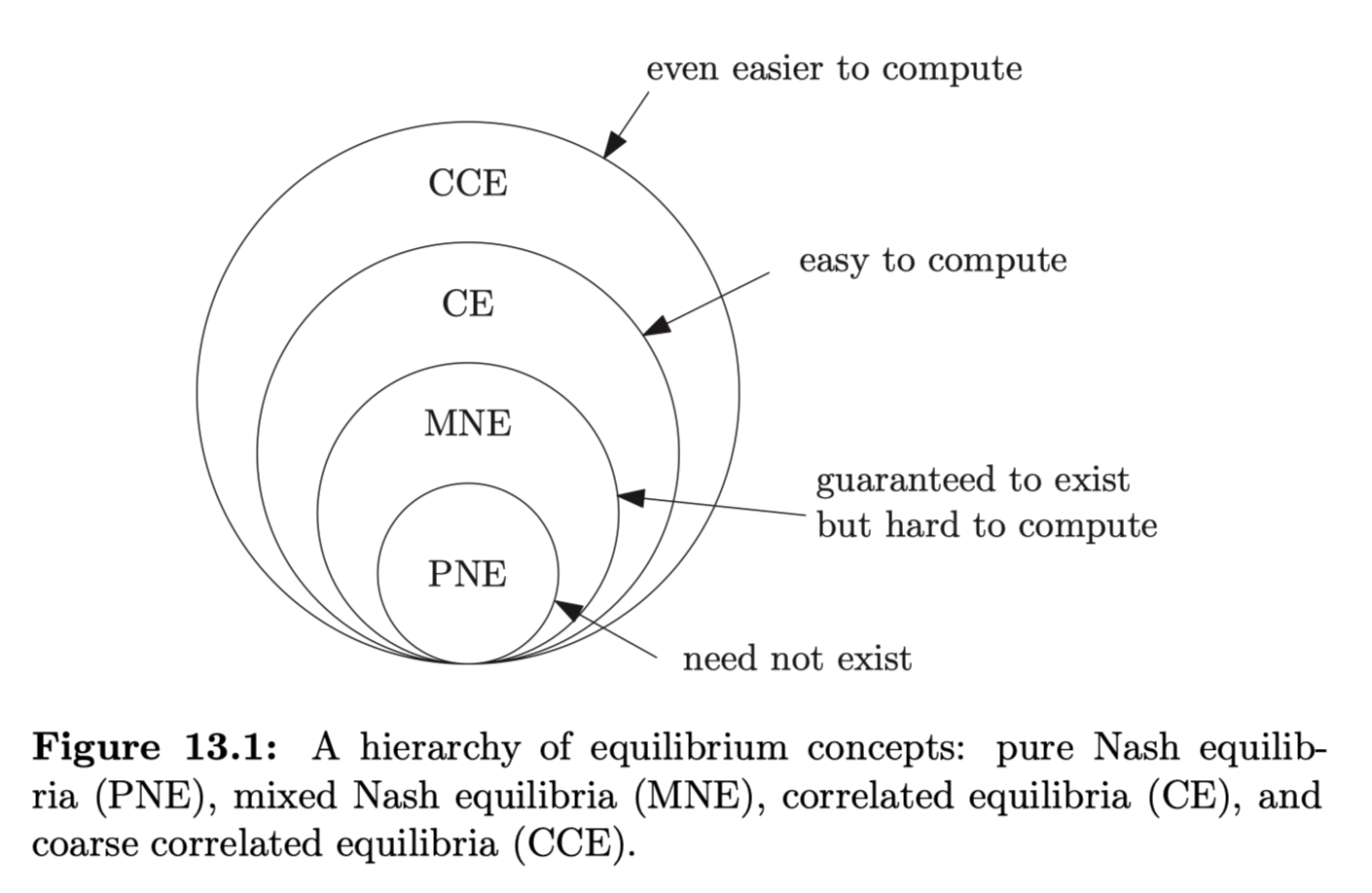
Intuition. Hierarchy of Games in game theory.

Pure Strategy §

def. Pure Strategy Nash Equilibrium is a set of strategies (one for each player) which is the best response strategy of each other’s move; i.e. you can’t deviate without destabilizing the equilibrium.

$${\forall }_{i\in \text{Players}},s_i={\text{argmin}}_{s\in S_i}{c}_1(s,\overrightarrow{s_{-i}})$$

where:

• ${\vec{s}}_{-i}$: strategies of all other players (excluding $i$-th player)
• $s$: strategy for $i$-th player
• $S$: strategy set for $i$-th player
• $c_i(\vec{s})$: cost function for $i$-th player

How to Find PNE §

• In Simultaenous Games: Use the Corner method
• In Sequential Games:
  • Make the Decision Tree into a Payoff Matrix, and use the Corner method
  • Just test out every combination of Strategy

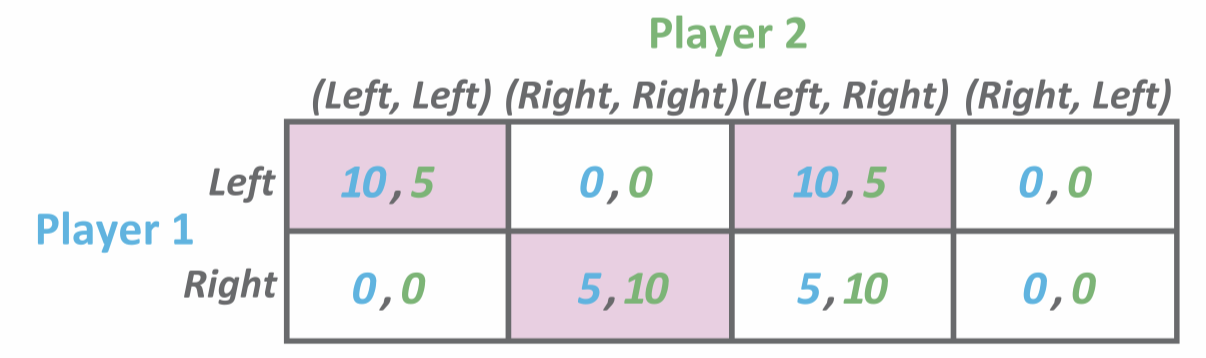
alg. Corner Method to find NE. Finding the Nash Equilibrium in a payoff matrix.

1. For each player:
2. For each other player’s move; highlight the line of the best response → When both the left and top lines are highlighted that is NE.

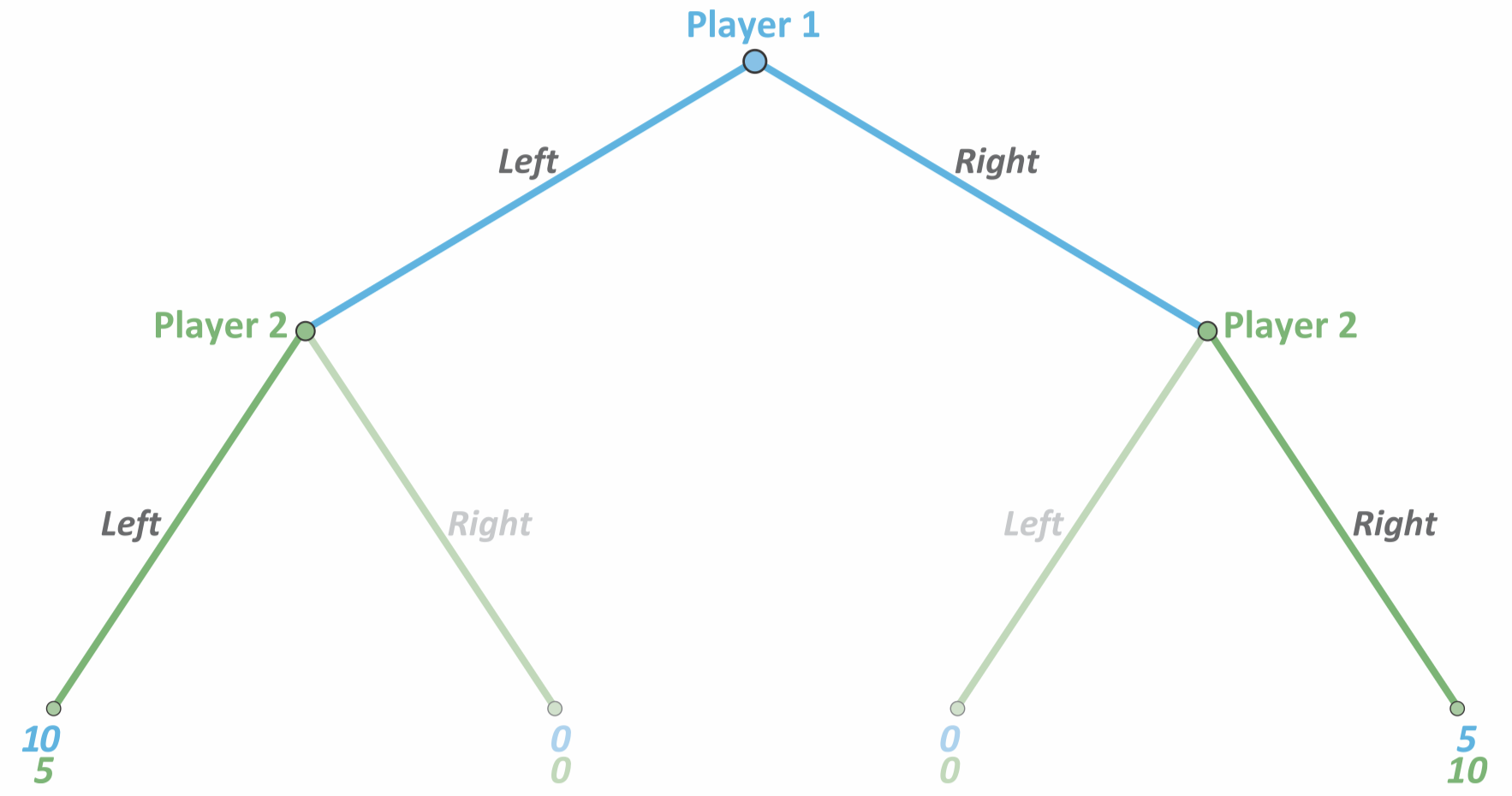
Example. Driving left or Right:

Subgame Perfect Nash Equilibrium (for Pure Strategy) §

def. A Non-credible threat is when the follower in a sequential move game says: “If I can’t win, I’ll take you down no matter how much it costs to me.”

• In the above game, $(R,R)$ is an example of a non-credible threat because when Player 1 chooses L, Player 2’s best response is L—but Player 2 threatens to go R. This is because they want the best possible outcome for them, $R,(R,R)$

def. Subgame Perfect Nash Equilibria (SPNE) are NE where the follower will only choose strategies that are best for them, and can’t threaten the leader beforehand with non-credible threats.

alg. Backwards Induction. To find the SPNE of a game, use Backwards Induction:

1. Determine the last player’s best strategy
2. The second-last player knows what the last player will do. Then determine what the second-last player will do.
3. Continue solving until the first player.

• Example. Caterpillar game unraveling
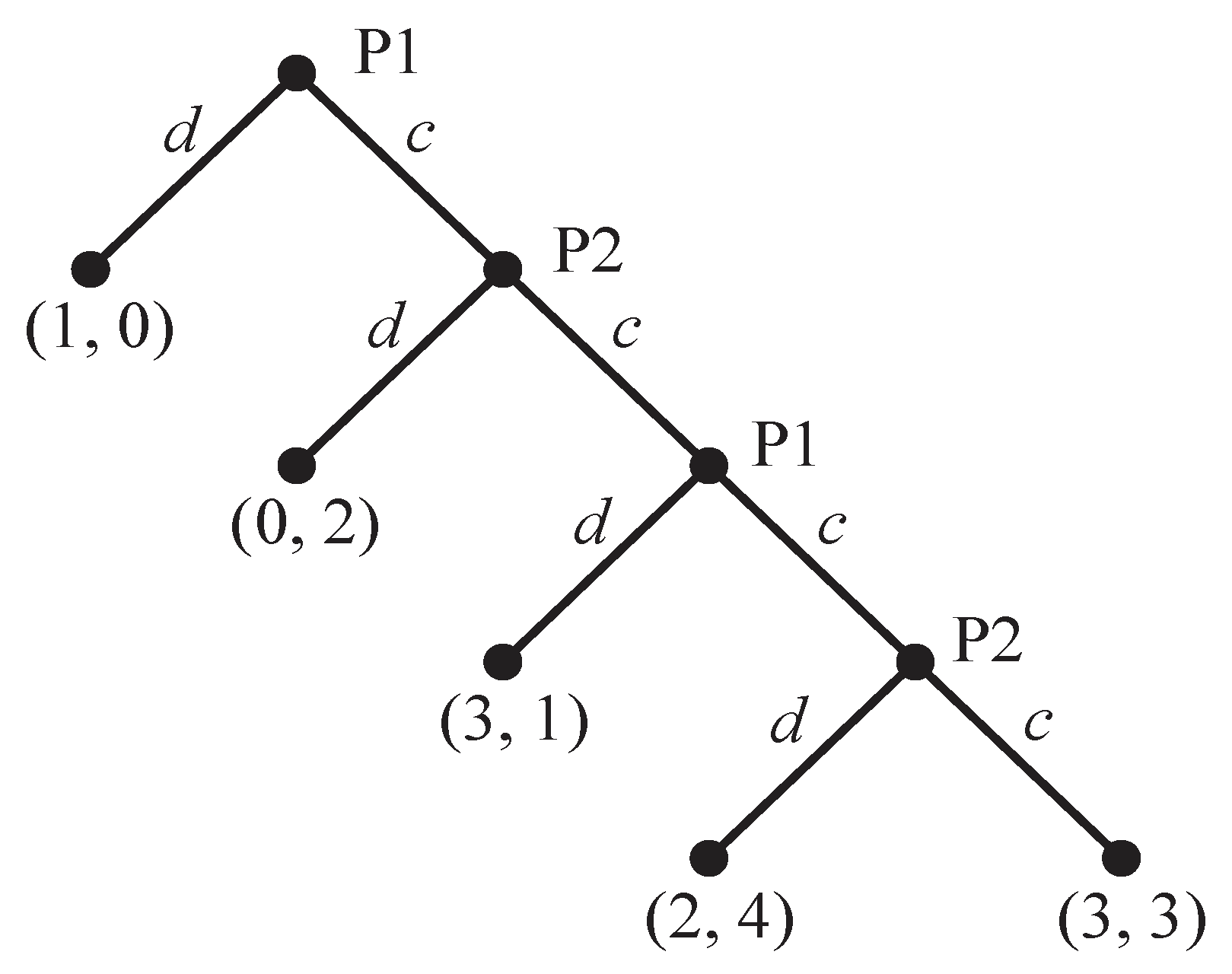
• $SPNE=\{(d,d),(d,d)\}$, payoff is (1,0) which is a lot worse off that global optimal.

Mixed Strategy Nash Equilibrium §

def. Mixed Strategy Nash Equilibrium

1. Each player $i$ chooses a distribution ${\sigma }_i$ over strategy set $S_i$ ← ${\sigma }_i$ is public knowledge
2. At runtime, each player chooses strategy $s_i\sim {\sigma }_i$ independent of other players
3. $(s_1,\dots ,s_n)$ is a Mixed Nash Equilibrium if:

$${\forall }_i\forall s_i\in S_i,\underset{\text{Expected cost after switching}}{\underbrace{E_{{\vec{s}}_{-i}\sim {\vec{\sigma }}_{-i}}[C_i(s_i^{\prime },\overrightarrow{s_{-i}})]}}\ge \underset{\text{Expected cost of potential equal. strat.}}{\underbrace{E_{{\vec{s}}_{-i}\sim {\vec{\sigma }}_{-i}}[C_i(s_i,\overrightarrow{s_{-i}})]}}$$

thm. (Existence of MNE, John Nash) Any game with finite players and finite set of strategies for each player has an MNE. Proof. The proof as three parts: the proof of Sperner’s Lemma, using it to prove Brouwer’s Fixed Point Theorem, and then reducing a mixed Nash Equillibrium to a fixed point in Brouwer’s Fixed Point theorem. We will only reveal the last part in this proof. Consider the following:

• Agent $i$ has the strategy set $S_i$. There are $k$ agents. Their payoff is ${\pi }_i(S_i,S_{-i})$.
• ${\Delta }_i:=(p_1,p_2,\dots )$ is the mixed strategy set of agent $i$ with each corresponding to the probability of each strategy in $S_i$.
  • This makes it a unit simplex in ${\mathbb{R}}^{|S_i|}$
• $C:={\Delta }_1\times \cdots \times {\Delta }_k$ is all possible combinations of mixed strategy of all agents.
  • $C$ is a compact set, and we want to apply Brouwer’s theorem on this space Let function $f_i:\underset{\text{ combination of mixed strat. }}{\underbrace{C}}\mapsto \underset{\text{ i’s mixed strat. }}{\underbrace{{\Delta }_i}}$ be:

$$f_i(x_i,\overrightarrow{x_{-i}}):=\underset{\text{ maximize, return mixed strategy x′ }}{\underbrace{\arg \underset{x^{\prime }\in {\Delta }_i}{\max }}}\underset{\text{ ...that maximizes expected payoff }}{\underbrace{\mathbb{E}({\pi }_i(S))}}-\underset{\text{ regularizaer (don’t move fast) }}{\underbrace{\mid \mid x_i^{\prime }-x_i\mid {\mid }_2^2}}$$

Then, let function $f:C\mapsto C$ be defined $f(\vec{x})=(f_1(x_1),f_2(x_2),\dots ,f_k(x_k))$. Then $f$ is continuous, thus there exists a point in which $f({\vec{x}}^{\ast })=\overrightarrow{x^{\ast }}$. This means at $\overrightarrow{x^{\ast }}$ there is no more expected payoff maximization that can be made by any individual, i.e. MNE. ■

alg. Computation of MNE using Linear Programming.

• The payoff matrix denotes what the column player (=minimizing player) gives to row player (=maximizing player)

1. Row player thinks that column player will minimize exchange (stackleberg solution)
2. Column player thinks that row player will maximize exchange (stackleberg solution)
3. Strategy tuple that satisfies both conditions is an MNE.

Correlated Nash Equilibrium (CNE) §

def. Correlated Nash Equilibrium

1. 3rd party computes joint distribution of all parties $S_1\times S_2\times \cdots \times S_n$, to joint distribution $\sigma$ ← this joint distribution is public knowledge.
2. At runtime, 3rd party draws strategy vector $\vec{s}=(s_1,s_2,\dots ,s_n)\sim \sigma$
3. 3rd party tells player $i$ to play $s_i$
4. Player $i$ computes the posterior distribution of what other players will do: ${\sigma }_{-i}$
5. $(s_1,\dots ,s_n)$ is a Correlated Nash Equilibrium iff:

$${\forall }_i\forall s_i\in S_i,\underset{\text{Expected cost after switching}}{\underbrace{E_{{\vec{s}}_{-i}\sim {\vec{\sigma }}_{-i}}[C_i(s_i^{\prime },\overrightarrow{s_{-i}})]}}\ge \underset{\text{Expected cost of potential equal. strat.}}{\underbrace{E_{{\vec{s}}_{-i}\sim {\vec{\sigma }}_{-i}}[C_i(s_i,\overrightarrow{s_{-i}})]}}$$

alg. CNE Computation Using Integer Linear Programming:

Example of Correlated Nash Equilibirum: Traffic Lights game:

Imperfect Information §

Baysian Nash Equilibrium §

In a

• mixed strategy (players each have probability of action)

• one-shot game def. Baysian Nash Equilibirum is a set of strategies that are mutual best responses given a certain probability of other’s actions

• For a BNE to exist, each person’s strategy must assign probabilities such that the opponent is neutral to each of their options. (if not, it means there is a dominant strategy for the opponent)

def. Perfect Baysian Equilibirum. In a mixed strategy, finitely repeated game, with each player having a belief a Perfect Baysian Equilibirum is one that

• the player’s beliefs are consistent with strategy (rational)
• is a BNE for each subgame → Signaling Game is a good example