Relational Algebra

(DevonThink) 2. Relational Algebra

Mathematical formulation of operations on relational data.

• Made by E.F. Codd
• Equivalent to domain-independent relational calculus
  • Relational calculus is a specialization of first-order logic
• Isn’t Turing-complete because it lacks recursion.
  • But because of this, relational algebra is decidable
• High level and declarative (procedural implementation is left to DBMS)
• Easy to optimize by the DBMS

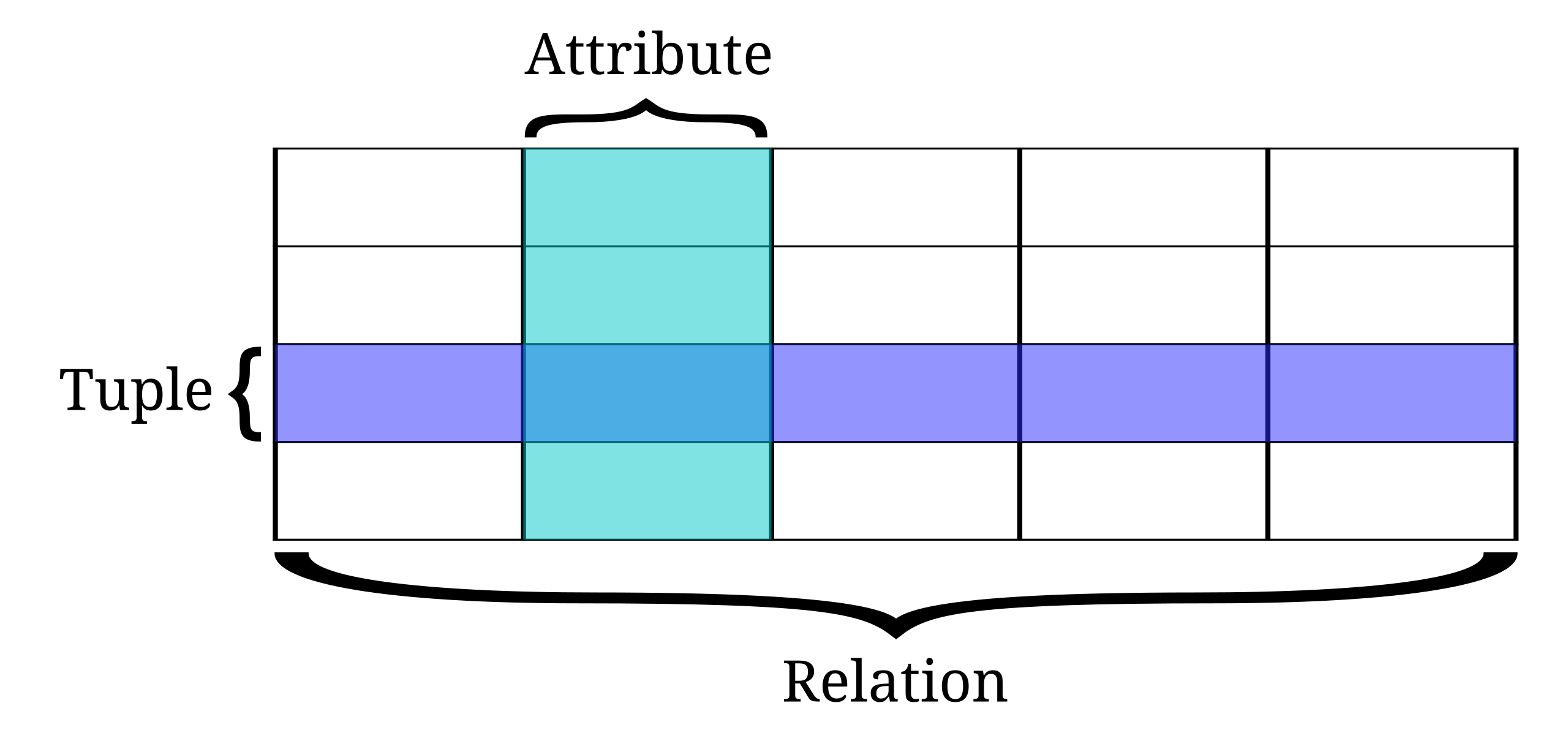
Definitions §

DBMS jargon	Common-sense name
Relation	Table
Attribute	Column
Domain	Data type
Tuple	Row

• A row is defined as a tuple
  • Duplicate rows are not allowed
  • A tuple is considered same if all attributes are same.
• Schema: the tuple of attribute names ($\approx$class)
• Instance: the instantiation of the schema ($\approx$object)
• Key (see below for formal definition):
  • e.g. address(street_addr,city,state,zipcode)
    • ⇒ {street_addr,city,state} is a key
      • ..but {street_addr,state} is not a key
    • ⇒ {street_addr,zipcode is also a key

def. Superkey. A set of attributes $K$ is a superkey of relation $R$ if there exists a dependency:

def. Key. A superkey $K$ is a key of relation $R$ if there is no other superkey with smaller number of attribute elements. (=minimally identifies each tuple/row)

alg. Determining if a superkey is a key.

1. Reduce one element and see if the key is superkey.
2. If a reduction of one element doesn’t yield a smaller superkey, we got it.
3. If it does, recurse.

Relational Operators §

Fundamental Operations §

• Selection: ${\sigma }_p\cdot R$
  • “Give me the entries of relation $R$ that satisfies condition $p$”
• Projection: ${\pi }_L\cdot R$
  • “Give me the attribute $L$ for each entry of relation $R$”
  • Duplicates are filtered out
• Cross Product: $R\times S$
  • Same as cross product of normal sets.
  • ⇒ Every row of $R$ per every row of $S$
• Union: $R\cup S$
  • $R,S$ must have identical schema
  • All rows on $R,S$ combined
  • Duplicates are removed
• Difference: $R-S$
  • $R,S$ must have identical schema
  • Rows in $R$ that are not in $S$
• Renaming: ${\rho }_S\cdot R$
  • Rename attribute $S$ of relation $R$

Derived Operators §

• Join [=Theta Join]: ${\bowtie }_p$
  • definition: ${\sigma }_p(R\times S)$
  • “Cross Product the relations, and then filter by condition $p$”
  • i.e. “Join the two databases so based on condition”
• Natural-Join: $\bowtie$
  • definition: ${\pi }_L(R{\bowtie }_{p}S)$
    • where $p$ pairs common attributes
    • where $L$ is the union of the attribute names
  • “Theta join, but the duplicate attribute is removed”
• Outer-Join
  • Left outer join: $R⟕S$ (leave null entries from $R$)
  • Right outer join: $R⟖S$ (leave null entries from $S$)
  • Full outer join: $R⟗S$ (leave null entries from $R,S$ both)
• Intersection: $R\cap S$
  • $R,S$ must have identical schema
    • defined as $R-(R-S)\equiv S-(S-R)$
• Symmetric Difference: $(R-S)\cup (S-R)$

Monotonicity §

(Vaguely related to: Monotonic Transformation)

def. Monotonic Operation. If input adds more rows, does the output also only add more rows? i.e. $f$ is a monotone operator iff:

$$R\subseteq R^{\prime }⟹f(R)\subseteq f(R^{\prime })$$

• Difference ($R-S$) is the only non-monotone operator among simple operators
  • Monotone for $R$ but not for $S$
• If an operation is not monotone, it must include the difference operator.

Expression Tree Notation §

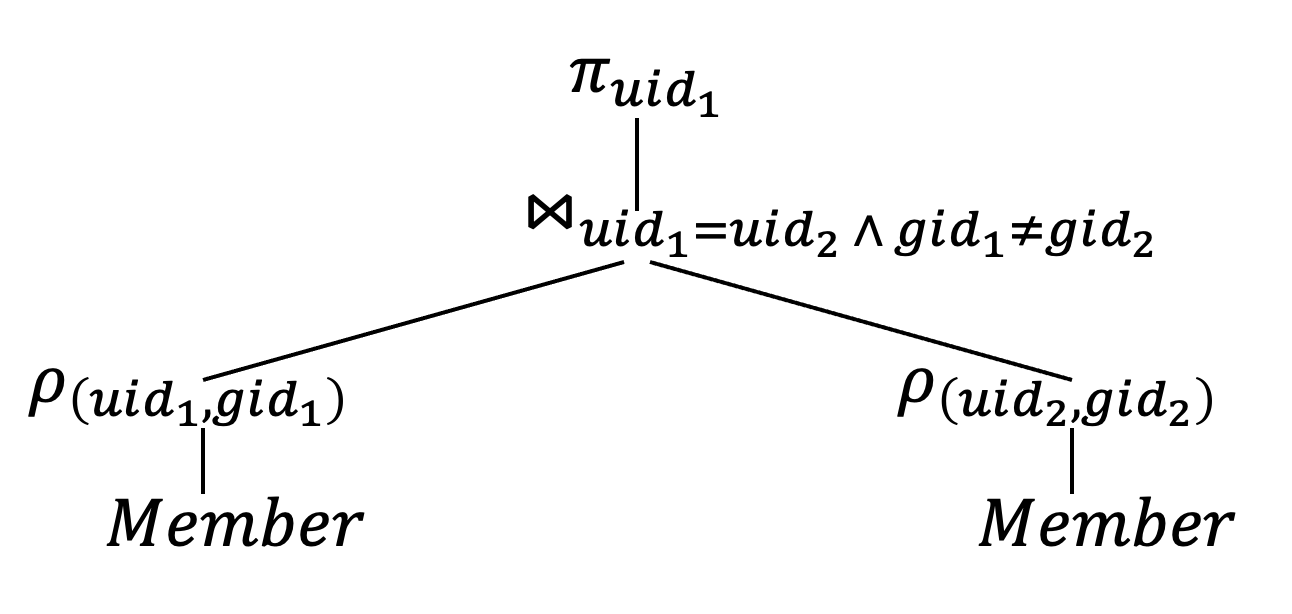
• Simpler to use and understand
• Designed both bottom-up or top-down

Properties of Relational Algebra §

1. Selection Properties

   • Idempotent: ${\sigma }_A(R)={\sigma }_A{\sigma }_A(R)$
   • Commutative: ${\sigma }_A{\sigma }_B(R)={\sigma }_B{\sigma }_A(R)$
   • Conjunction: ${\sigma }_{A\wedge B}(R)={\sigma }_A({\sigma }_B(R))={\sigma }_B({\sigma }_A(R))$
   • Disjunction: ${\sigma }_{A\vee B}(R)={\sigma }_A(R)\cup {\sigma }_B(R)$
   • Breaking up: ${\sigma }_A(R\times P)={\sigma }_{B\wedge C\wedge D}(R\times P)={\sigma }_D({\sigma }_B(R)\times {\sigma }_C(P))$
   • Distribution over Difference: ${\sigma }_A(R\setminus P)={\sigma }_A(R)\setminus {\sigma }_A(P)={\sigma }_A(R)\setminus P$
   • Distribution over Union: ${\sigma }_A(R\cup P)={\sigma }_A(R)\cup {\sigma }_A(P)$
   • Distribution over Intersection: ${\sigma }_A(R\cap P)={\sigma }_A(R)\cap {\sigma }_A(P)={\sigma }_A(R)\cap P=R\cap {\sigma }_A(P)$

2. Selection and Projection Commutativity

   • ${\pi }_{a_1,\dots ,a_n}({\sigma }_A(R))={\sigma }_A({\pi }_{a_1,\dots ,a_n}(R))$ where fields in $A\subseteq \{a_1,\dots ,a_n\}$

3. Projection Properties

   • Idempotent: ${\pi }_{a_1,\dots ,a_n}({\pi }_{b_1,\dots ,b_m}(R))={\pi }_{a_1,\dots ,a_n}(R)$ where $\{a_1,\dots ,a_n\}\subseteq \{b_1,\dots ,b_m\}$
   • Distributing on Union: ${\pi }_{a_1,\dots ,a_n}(R\cup P)={\pi }_{a_1,\dots ,a_n}(R)\cup {\pi }_{a_1,\dots ,a_n}(P)$
   • ! Projection doesn’t distribute along difference:
     • ${\pi }_A(\{⟨A=a,B=b⟩\}\setminus \{⟨A=a,B=b^{\prime }⟩\})=\{⟨A=a⟩\}$
     • ${\pi }_A(\{⟨A=a,B=b⟩\})\setminus {\pi }_A(\{⟨A=a,B=b^{\prime }⟩\})=\varnothing$
   • ! Projectio doesn’t distribute along intersection:
     • ${\pi }_A(\{⟨A=a,B=b⟩\}\cap \{⟨A=a,B=b^{\prime }⟩\})=\varnothing$
     • ${\pi }_A(\{⟨A=a,B=b⟩\})\cap {\pi }_A(\{⟨A=a,B=b^{\prime }⟩\})=\{⟨A=a⟩\}$

4. Rename Properties

   • ${\rho }_{a/b}({\rho }_{b/c}(R))={\rho }_{a/c}(R)$
   • ${\rho }_{a/b}({\rho }_{c/d}(R))={\rho }_{c/d}({\rho }_{a/b}(R))$
   • Distribution on Difference: ${\rho }_{a/b}(R\setminus P)={\rho }_{a/b}(R)\setminus {\rho }_{a/b}(P)$
   • Distribution on Union: ${\rho }_{a/b}(R\cup P)={\rho }_{a/b}(R)\cup {\rho }_{a/b}(P)$
   • Distribution on Intersection: ${\rho }_{a/b}(R\cap P)={\rho }_{a/b}(R)\cap {\rho }_{a/b}(P)$

5. Product and Union

   • Cartesian Product and Union: $(A\times B)\cup (A\times C)=A\times (B\cup C)$