Joint Distributions

Discrete Joint Distribution §

def. Joint Distributions of two discrete random variables $X,Y$ encode the probabilities for every pair of $(x,y)$ for $(X,Y)$. Following is an example of a joint distribution where $X$ is the result of rolling a first dice and $Y$ the result of a second roll.

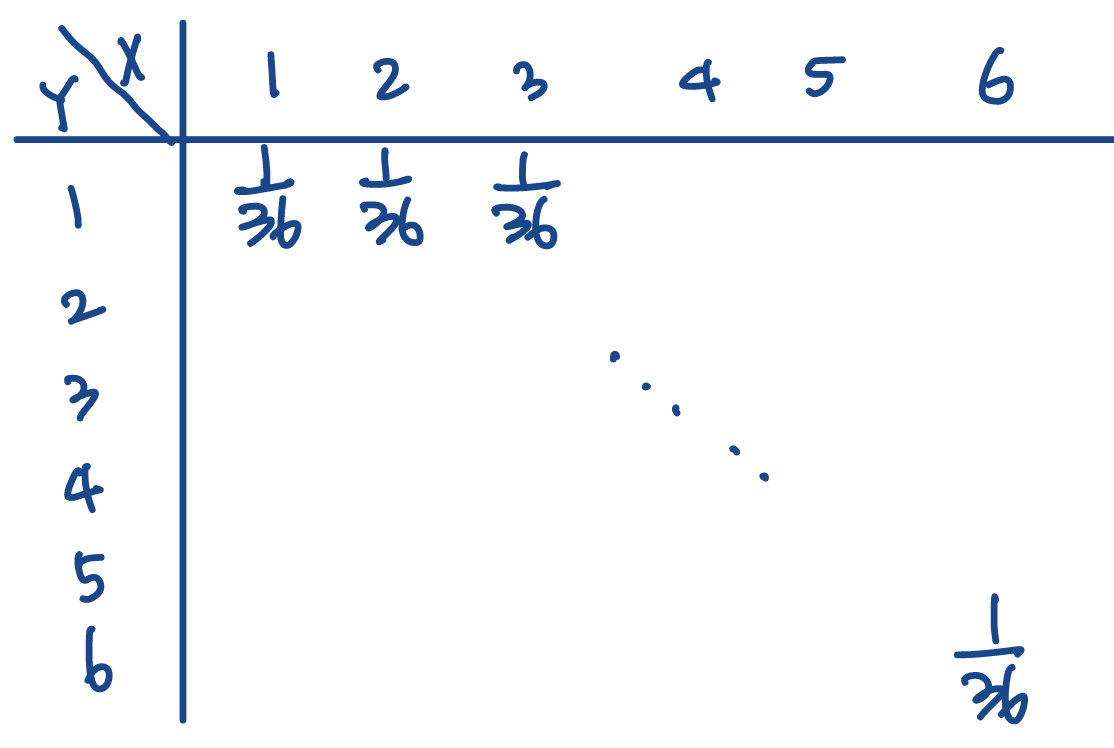
REMARK. Joint Distributions are distributions too, which means it has to follow all the rules of distributions (e.g. $\sum =1$)

Continuous Joint Distribution §

def. Joint Probability Density. Let $X,Y$ be two independent continous random variables. Then the joint probability density function is defined as the derivative of the cumulative density function:

$$f_{X,Y}(x,y):=\frac{{\partial }^2{F}_{X,Y}(x,y)}{\partial x\partial y}$$ $$\begin{gathered} f_{X,Y}(x,y)\Delta x\Delta y=\mathbb{P}((x,y)\in R) \\ \therefore f_{X,Y}(x,y)=\underset{\Delta x,\Delta y\to 0}{\lim }\frac{\mathbb{P}(x,y)\in R}{\Delta x\Delta y} \end{gathered}$$

And thus the following holds:

• $\mathbb{P}((x,y)\in R)={\iint }_{R}f(x,y)dA$ where $R$ is an event
• ${\iint }_{{\mathbb{R}}^2}fdA=1$
• $X\perp Y\iff f_{X,Y}=f_X\cdot f_Y$

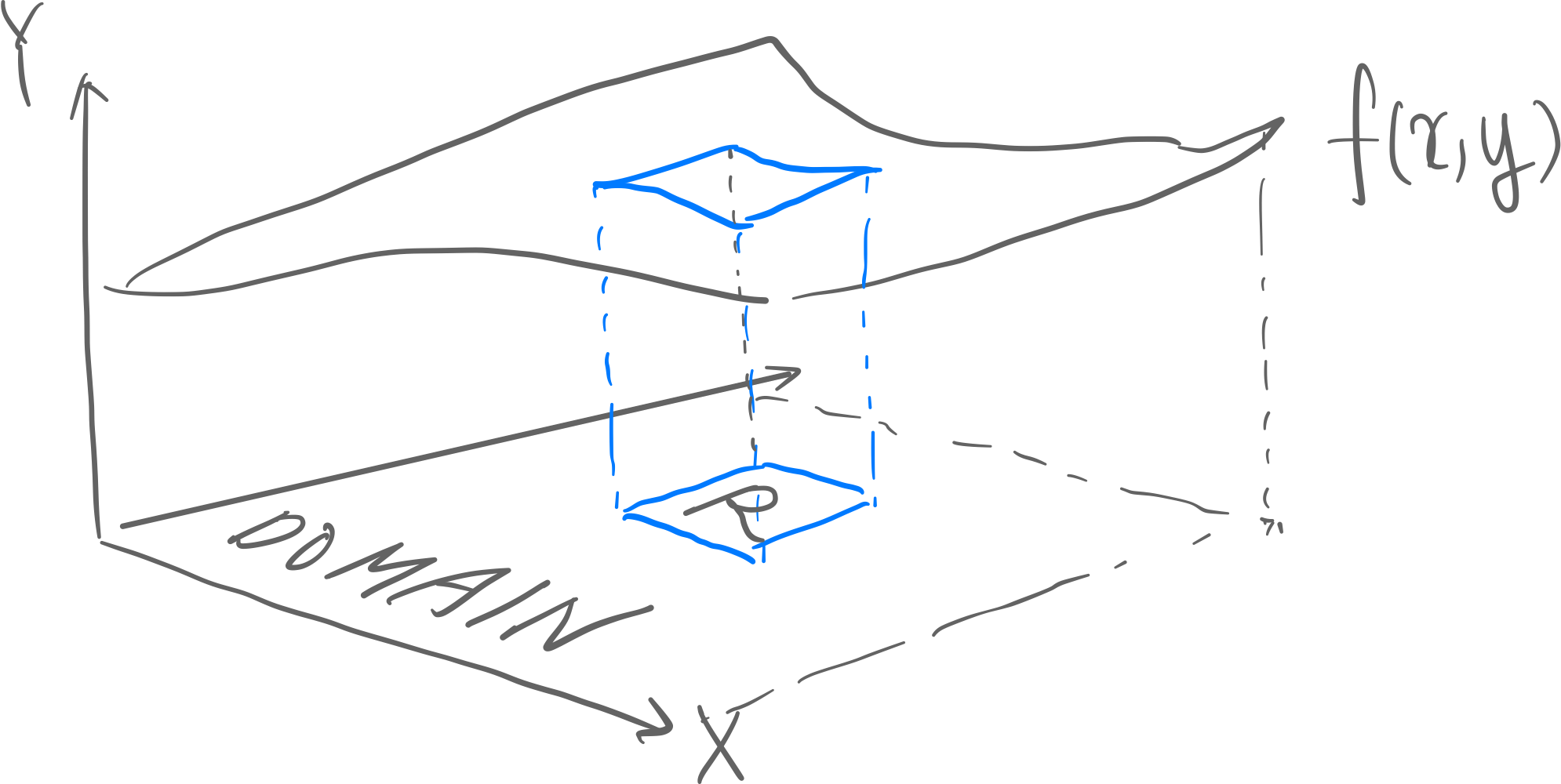
The blue volume in the picture is the probability of the event X and Y are in R.

• See Joint Marginal Distribution
• See Joint Expected Value

Full Visual Example §

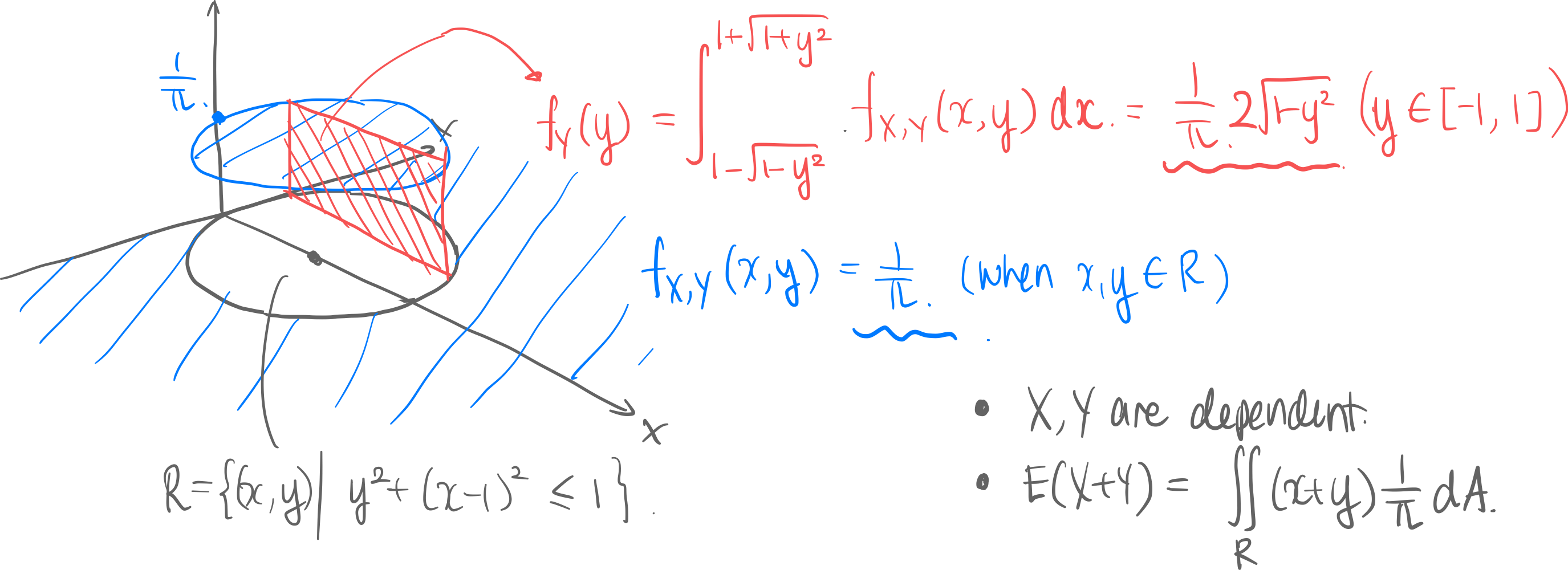
• Blue is the probability density function, $f_{X,Y}(x,y)=\{\begin{array}{ll}\frac{1}{\pi }& (x-1{)}^2+y\le 1\\ 0& \text{else}\end{array}$
• Red is the marginal probability density of $Y$,

$f\ast Y(y)=\{\begin{array}{ll}\int \ast {x=1-\sqrt{1-y^2}}^{1+\sqrt{1+y^2}}f\_X,Y(x,y)dx& y\in [-1,1]\\ 0& \text{else}\end{array}$

Minimum and Maximum Joint Dist §

thm. Let $X_1,\dots X_n$ be i.i.d.; let $P=\text{min}(X_1,\dots ,X_n),Q=\text{max}(X_1,\dots ,X_n)$. Then:

$$f_{P,Q}(p,q)=\{\begin{array}{ll}n(n-1)\cdot f_{X_i}(p)\cdot f_{X_i}(q)\cdot [{\int }_p^q{f}_{X_i}(x)dx{]}^{n-2}& y<z\\ 0& else\end{array}$$

---

Examples of Joint Distributions §

Tip

Recall that joint distributions are also distributions [=encapsulate fully the information of an experiement].

Uniform Joint §

thm. If $X,Y$ are both uniformly distributed over $[x_1,x_2],[y_1,y_2]\equiv \Omega$, then…

• height of the distribution is $\frac{1}{|\Omega |}$ (where $|\Omega |$ denotes the area of the outcome space.)
• $\mathbb{P}((x,y)\in R)=\frac{|R|}{|\Omega |}$

Normal Joint (Linear Combination) §

thm. Linear Combination of Normal Distributions. If $X_1\sim N({\mu }_1,{\sigma }_1)$ and $X_2\sim N({\mu }_2,{\sigma }_2)$ then:

$$\forall a,b\in \mathbb{R},a{X}_1+b{X}_2\sim N(a{\mu }_1+b{\mu }_2,a^2{\sigma }_1^2+b^2{\sigma }_2^2)$$

Normal Joint (Product) §

thm. if $X\sim N({\mu }_1,{\sigma }^2)$ and $Y\sim N({\mu }_2,{\sigma }^2)$ (i.e. std. dev. is the same) then

• $f_{X,Y}=f_X\cdot f_Y$
• Volume of sector $\theta$ from $({\mu }_1,{\mu }_2)$ is $\frac{\theta }{2\pi }$

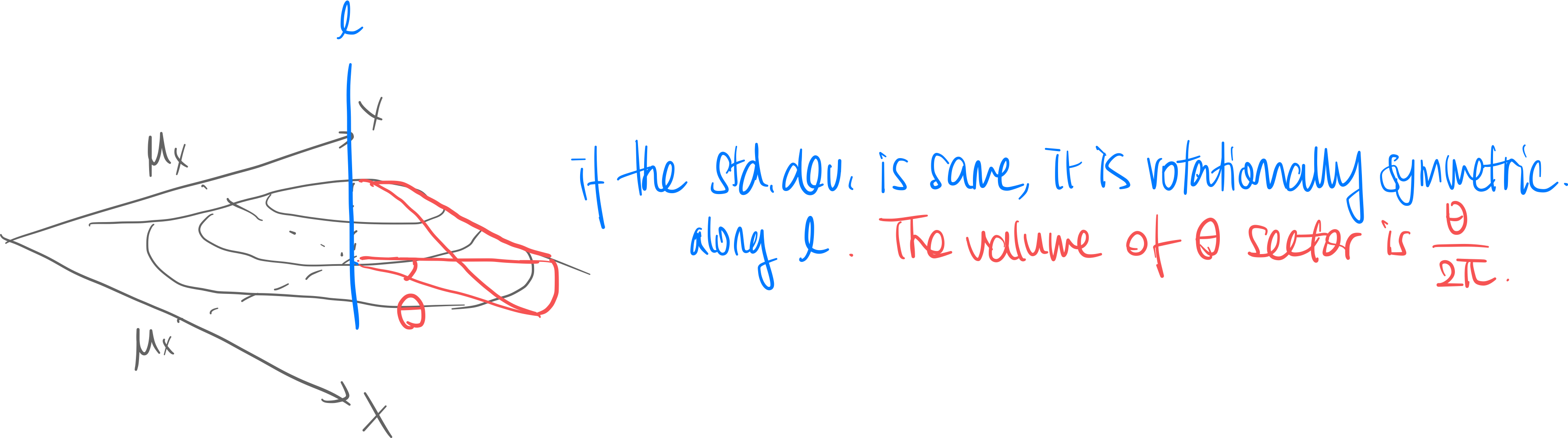
Rayleigh Distribution §

[=Squared & Rooted Joint Normal]

def. Rayleigh Distribution. let $X,Y\sim \text{Normal}(0,\sigma )$ and $W=\sqrt{X^2+Y^2}$, then:

$$\begin{array}{rl}W& \sim \text{Rayleigh}(\sigma )R\sim \text{RL}(\sigma )\\ f_R(r)& =\frac{r}{{\sigma }^2}{e}^{\frac{-r^2}{2\cdot {\sigma }^2}}\text{ for }r>0\\ F_R(r)& =1-e^{\frac{-r^2}{2\cdot {\sigma }^2}}\text{ for }r>0\\ \mathbb{E}(X)=\sigma \sqrt{\frac{\pi }{2}}& \mathbb{SD}(X)=\sigma \sqrt{\frac{4-\pi }{2}}\end{array}$$

• Where $\sigma$ is the “scaling factor” (standard dev. must be same for $X,Y$)
• If $\sigma =1$ then $W$ is a Standard Rayleigh distribution:

thm. Standardizing Rayleigh Distributions. If $W\sim \text{RL}(\sigma )$:

$$\frac{W}{\sigma }\sim \text{RL}(1)$$