Hashing Algorithms

def. Hash Function. A function that maps data to a hash table.

• Data is denoted $S\subset U$ (=Universe)
  • Universe can be continuous or discrete
• Hash table $T$ has $m$ slots, thus $T=[m]$
  • $[m]:=\{0,\dots ,m-1\}$, $[m{]}^{+}:=\{1,\dots ,m-1\}$
  • Access time is $O(1)$
• $h(x)$ is the hash function that takes in data point $x$

Uniform Hash Function §

def. Uniformity. A hash function is uniform iff:

$$\forall i\in [m],P[h(x)=i]=\frac{1}{m}$$

e.g. Modular Hash Function.

$$h(x)=x\text{ mod }m$$

• If $x$ is random, $P[h(x)=i]=\frac{1}{m}$

Universal Hash Function §

alg. Universal Hashing. A hash function is universal iff:

$$\forall x\ne yP[h(x)=h(y)]\le \frac{1}{m}$$

1. Initialization: Choose a random $h$ from family $H$
2. Use that $h(x)$ for all future hashing needs for that dataset ⇒ probability of collision is $\frac{1}{m}$

e.g. Universal Modular Hash Function.

def. Linear Congruence Hashing (integer key)

1. Choose a very large prime number $p$ (bigger than the number of things you need to hash=$|U|$)
2. Construct a hash table of size $m$
3. Construct a family of hash functions $H=\{h_{a,b}(x)=(ax+b\text{ mod}m)\text{mod}m\}|a,b<p$ ⇒ $H$ is a universal family

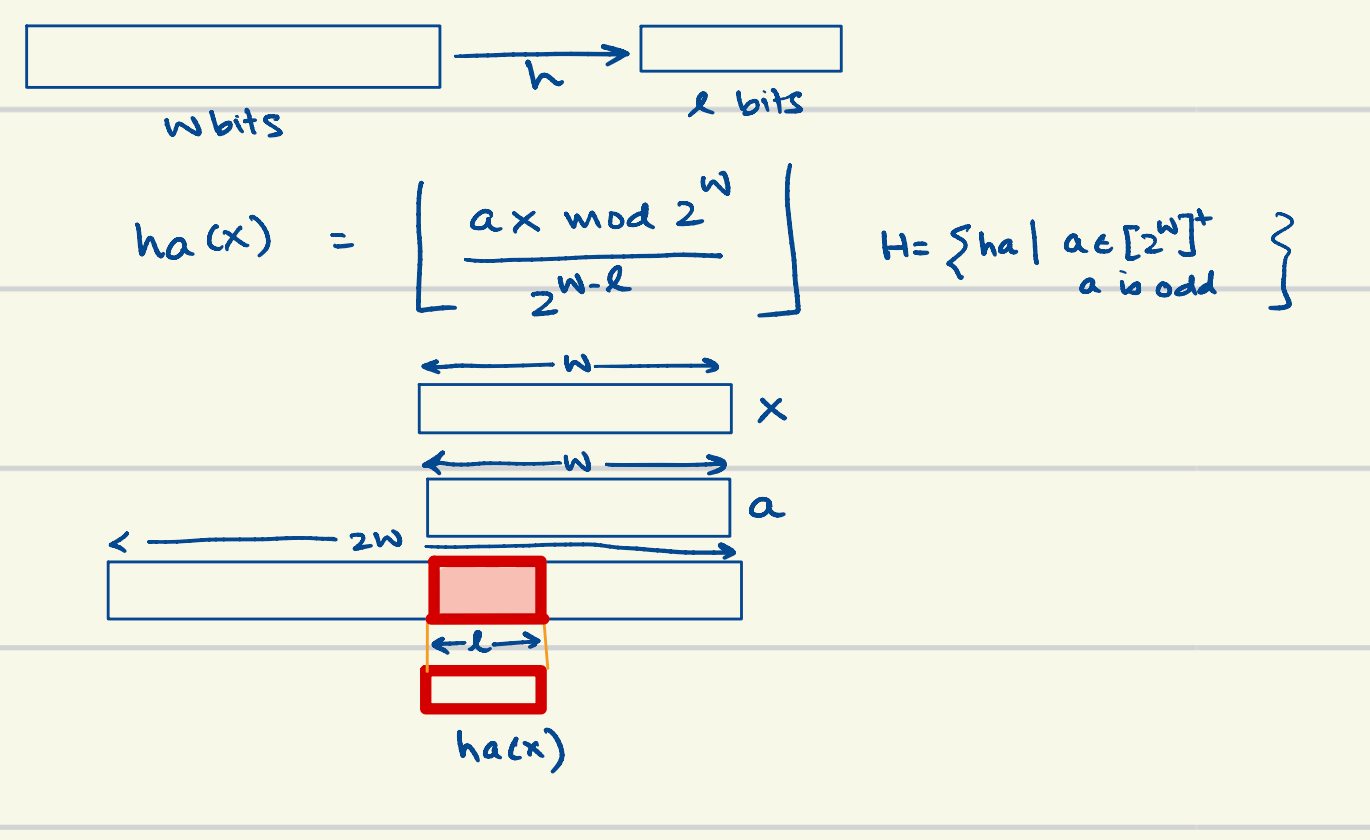
def. Multiply-Shift Binary Hashing (integer key) (SotA)

Collision §

def. Collision Probability.

Alternative Techniques §

Double Hashing §

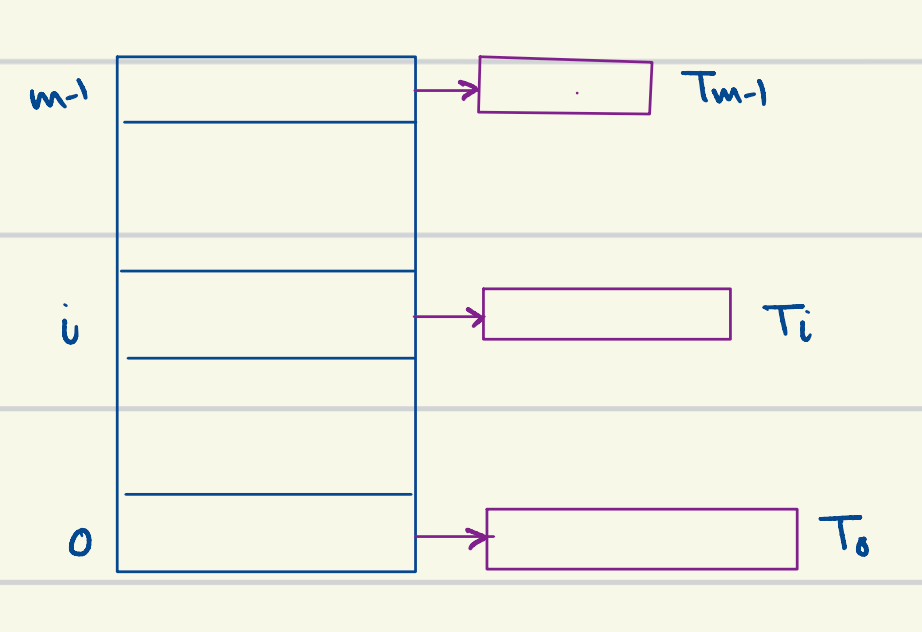
• Construction: $S\stackrel{h}{\to }T\stackrel{h_i}{\to }{T}_i$
• $T_i$: the secondary hash table
• $S_i$: set that denotes all the elements hashed to $T_i$. Depends on what $S$, the data, actually is
  • $E[S_i]\approx \frac{n}{m}$
  • For some slack, we usually make the secondary hash table $|T_i|=O(|S_i{|}^2)$

Bloom Filters §

1. From a family of hash functions $H$ choose $k$ different functions $h_1\dots h_k$
2. Initialize boolean array $T$ which has size $m$

• Insert(x)
  1. calculate $h_1(x),\dots h_k(x)$ and store them into $T[h_1(x)]\dots T[h_k(x)]$.
  2. If there’s alreay a $1$ in the table, keep it that way
• Search(x)
  1. calculate $h_1(x),\dots h_k(x)$
  2. If all of $T[h_1(x)]\dots T[h_k(x)]$ returns $1$, it’s highly likely that it is present.
  3. • (false positive rate=) Probability that search(x) returns True, even if $x\notin S$: $\approx (1-e^{-kn/m}{)}^k$……(1)
• (1)……$n$ is not really known. $m$ is limited by memory. So choose $k$ as big as possible
  • $k=\ln 2\cdot \frac{m}{n}$ is good ⇒ false positive search(x) is ${\approx }_0.$
• Probability that bit $B[j]=0$ is ${\left(1-\frac{1}{m}\right)}^{k|S|}$