A Turing machine:
- Is most powerful type of automation (probably.)
- Cannot solve the halting problem.
- Can be used to prove Limits of Math and Computing.
def. Turing Machine is a turing machine defined as a tuple:
where the previously unencountered symbols are:
- : States
- : Input Alphabet
- : Tape Alphabet (superset of )
- : Start state
- : Set of en states
- : Blank (also written as )
- Configuration and transition of a TM is denoted:
- Configuration:
- In this case the head is reading the first symbol of , i.e. the right-side letter.
- the ”” indicates a state transition
- Transition function :
- The configuration is denoted as
Turing Machines as Language Recognizers/Acceptors
def. Language of a turing machine. For turing machine with language , String if:
You can also think of it as the turing machine “halting” on the final state.
- If TM halts on a final state, is accepted
- If TM halts on a non-final state is not accepted
- If TM doesn’t halt, is not accepted
Turing Machines as a Transducer (=Transformation on a language)
def. Turing-Computable. A function is Turing-Computable if:
Example of a Turing Machine representing a turing-computable function:
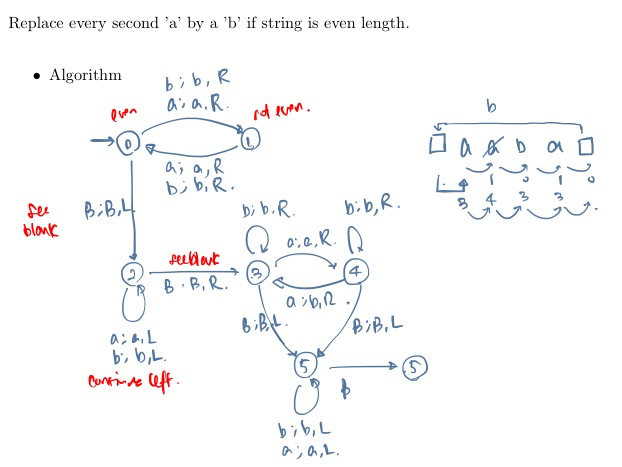
Turing Machine Building Blocks
- : run if is the current output ← you can also have multiple conditionals
You have the building blocks of commonly-used TMs.
- : start, : halt
- : write symbol onto tape
- : Move left, right
- : Move left or right until you see in tape ← make sure there is an on tape or it won’t halt
- Move left or right until you don’t see in input
- : symbols are represented as variable ← avoids having to write two identical machines for each symbol
Some more advanced building blocks:
- : Copy with a zero in the middle. e.g. . Tape head starts and ends in the beginning symbol.
- Shift left what is on the right, v.v. The symbol on the head is erased.
Example of using building blocks to simplify a turing machine:
Turing Machine Equivalents
- TM with Stay option:
- Multitrack TM: One tape, but split into cells:
- Diagram
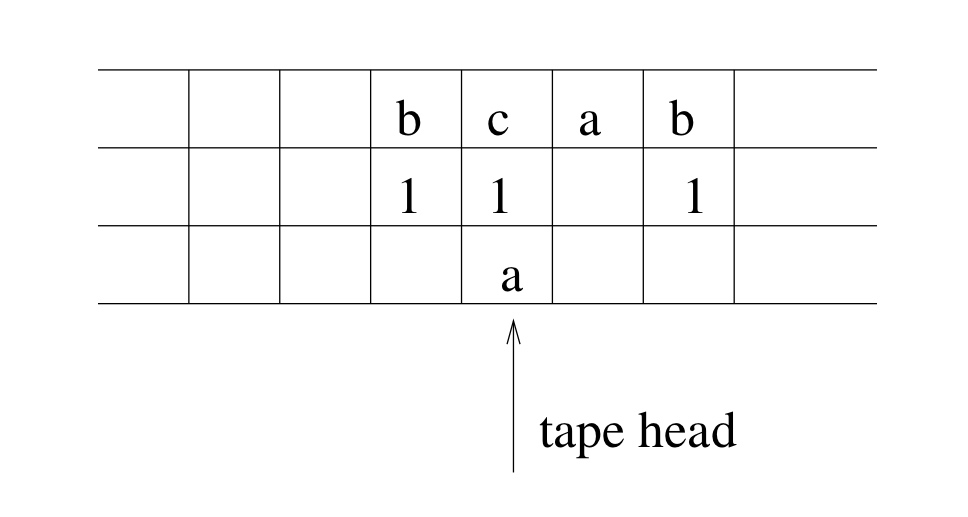
- Diagram
- Semi-infinite TM: The tape is infinite only in one direction → Proof by “folding over” the standard TM into multi-track.
- Multi-tape TM:
- Off-line TM: Two-tape; one tape is input, the other the read/write tape.
- Non-deterministic TM
- NPDA with 2 stacks
Universal Turing Machine
Every TM can be binary encoded by a binary number:
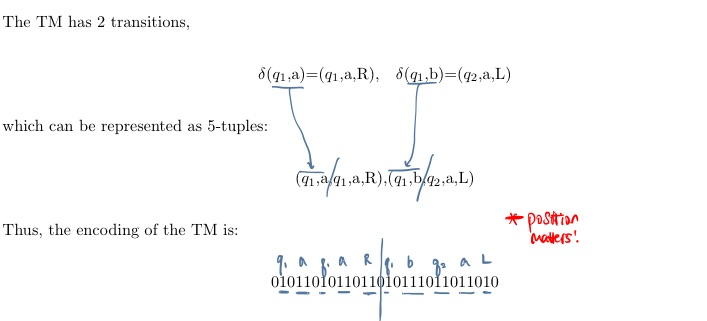
The Universal Turing Machine is a 3-tape turing machine that simulates a standard Turing Machine . Each of the tapes are:
- Tape A: Binary encoding of a simulation of
- Tape B: The tape of
- Tape C: ’s current state