Finite Automata

Regular Expressions

Definitions §

def. Automata is an abstract model of a computer.

def. Regular Language is a language that can be expressed by a FSM

def. Trap state is a state in which any symbol input leads to the same state.

def. Closure of $q_i$ is simply the set of states reachable from $q_i$ with only $\lambda$.

Deterministic Finite Automata (DFA) §

[= Finite State Machine]

$$\text{DFA}=(Q,\Sigma ,\delta ,q_0,F)$$

• $Q$ is the set of all states
• $\Sigma$ is the set of all symbols
• $\delta :Q\times \Sigma \to Q$ is a function mapping from current state to the next state
  • ${\delta }^{\ast }(q_i,\lambda )=q_i$ [= empty strings lead to itself]
  • ${\delta }^{\ast }(q,wa)={\delta }^{\ast }(\delta (q,w),a)$ where $a$ is a single symbol [= processes only one per tick]
• $q_0$ is the start state (entry point)
• $F$ is the set of final states

a,b.

def. Language. A string is accepted by a DFA when:

1. After processing the string, the DFA is in a final state
2. The string is in the language

The set of all aceepted strings by a DFA is the language of the DFA:

$$L(M)=\{w\in {\Sigma }^{\ast }|{\delta }^{\ast }(q_0,w)\in F\}$$

i.e. all the strings which, after processing it thru ${\delta }^{\ast }$, it lands on a final state

Non-deterministic Finite Automata (NFA) §

def. Non-deterministic Finite Automata can have multiple edges with the same labels; i.e.

$$\delta :Q\times \Sigma \cup \lambda \to 2^Q$$

i.e. from the current state, you can go to multiple states.

Example Non-deterministic FSM

corr. “there exists a walk between $q_i,q_j$ whose labels concatenate to $w$” is equivalent to:

$$q_j\in {\delta }^{\ast }(q_i,w)$$

thm. All NFA can be convered into a DFA which:

$$\begin{array}{rl}\text{DFA}=\{& \\ Q& =2^Q\\ \Sigma & \\ \delta & =Q_D\times \Sigma =Q_D\\ q_0& \\ F_D& =\{Q\in Q_D|\exists q_i\in Q\text{ where }{q}_i\in F_N\}\\ \}& \end{array}$$

Proving Regularity after Applying Properties §

e.g. let $L$ be a regular language. For all strings in $L$ replace one $a$ with $b$, and let this new language $L^{\prime }$. Is this a regular language?

pf. let $M$be a DFA for $L$.

1. Make a copy $M_1,M_2$ and enclose it in a new machine, $M^{\prime }$
2. For all $a$ arcs in $M_1$ write a $b$ arc to the corresponding destination state in $M_2$.
3. The start state for $M_1$ is $M^{\prime }$ start state.

Now, let

• $w=uav$, and $w^{\prime }=ubv$ where $w,u,v\in {\Sigma }^{\ast }$
• ${\delta }_1^{\ast }(q_0,u)=q_i$, ${\delta }^{\prime }(q_i,b)=q_j$, ${\delta }_2^{\ast }(q_j,v)\in F$ as we outlined above

1. If $w\in L$ then

→ proofs often involve duplicating the machine in some way.

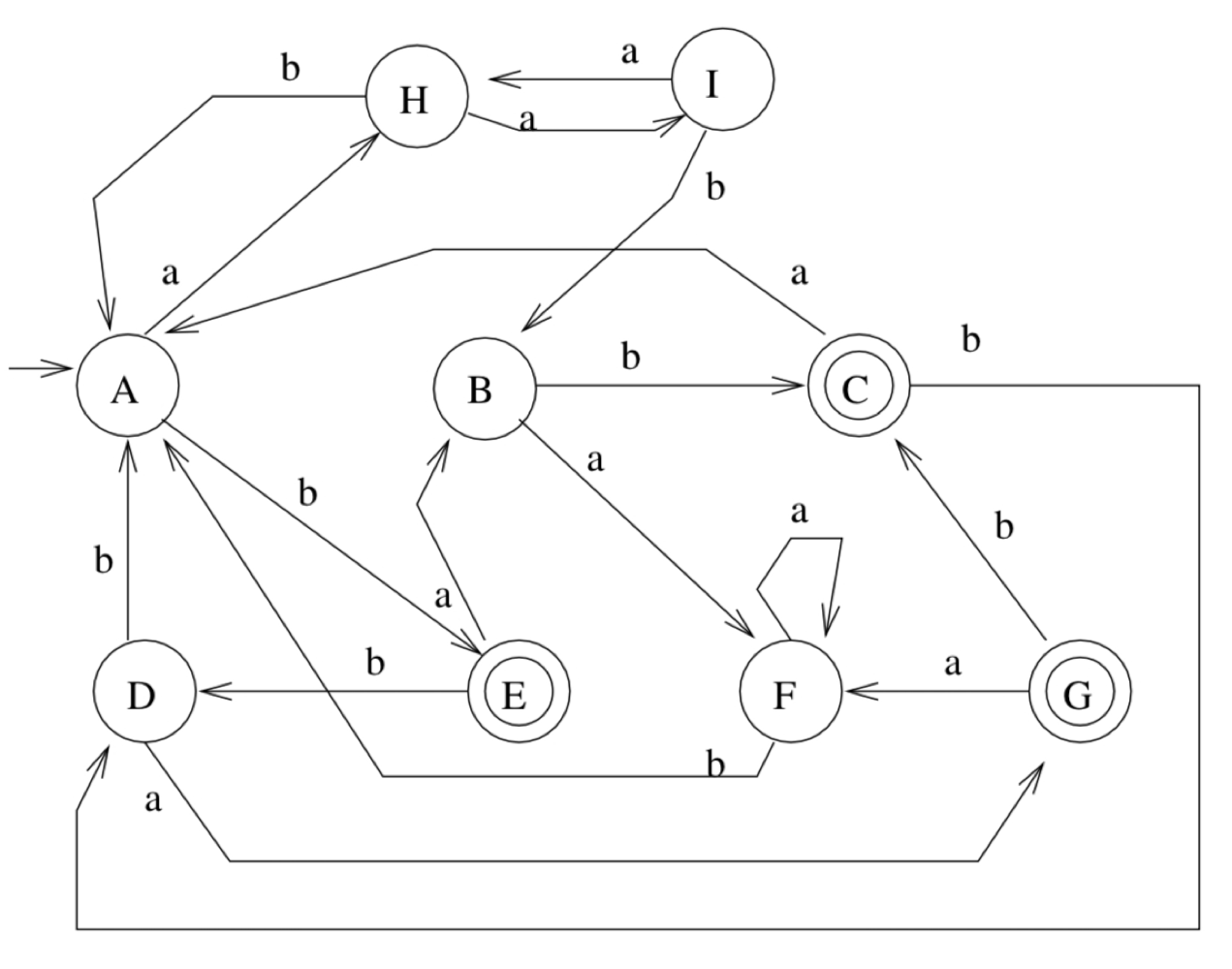
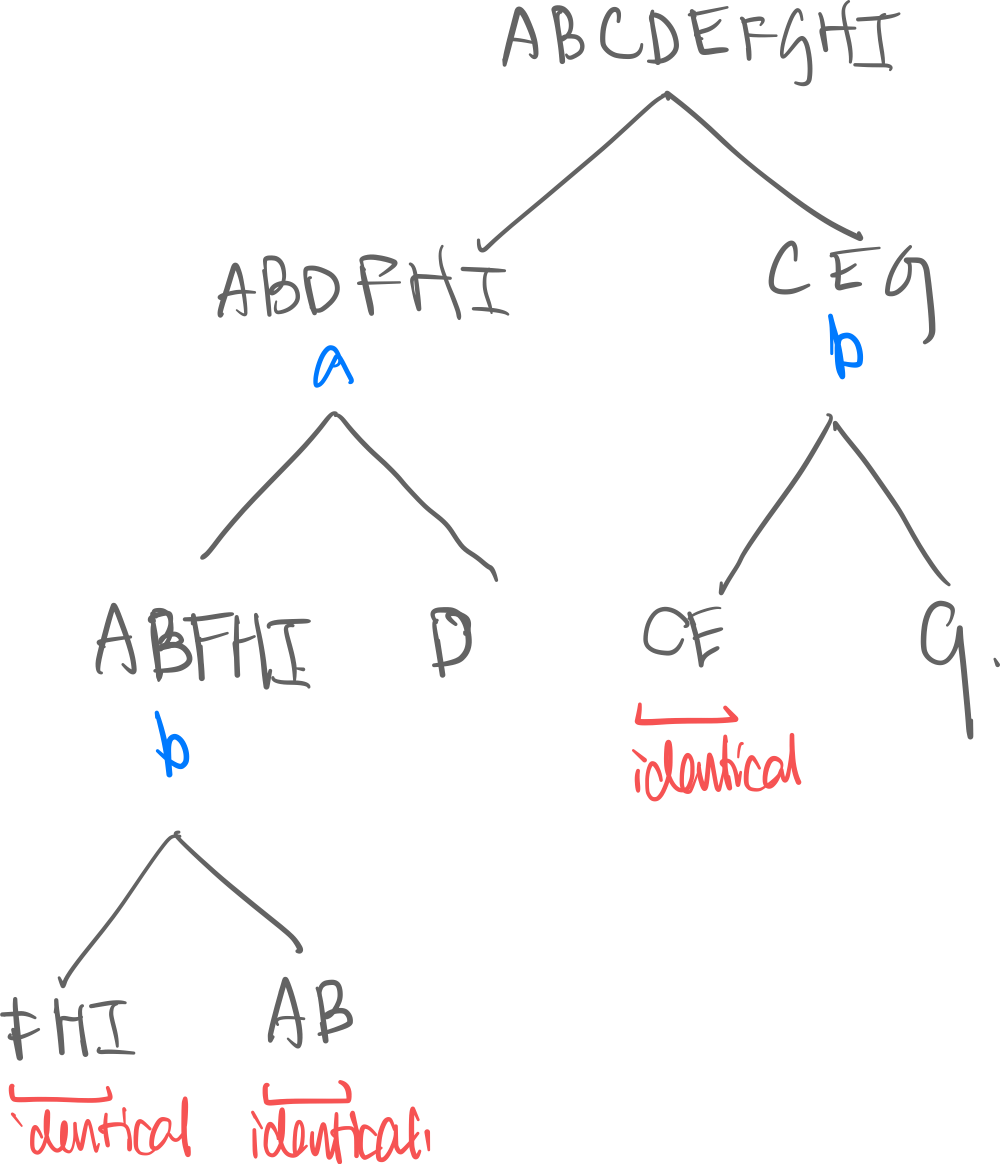
DFA Minimization §

Example: