Distribution (Math)

def. A distribution gives comprehensive information about an experiment. A distribution can be a table showing the probabilities of all outcomes, or a probability density function.

Moment Generating Function

def. let Ω be an outcome space. All functions $P(x)$ satisfying the following criteria are probability distributions.

Criteria:

1. $P(\varnothing )=0$ and $P(\Omega )=1$
2. For all $A\subseteq \Omega$, $0\le P(A)\le 1$
3. If A and B are disjoint then $P(A\cup B)=P(A)+P(B)$

The 3rd condition can also be generalized for any distributions:

• If $A_1,\dots ,A_n$ are pairwise disjoint, then $P(A_1\cup \cdots \cup A_n)=P(A_1)+\dots +P(A_n)$.

Remark. The distribution $P(A)=\frac{\#A}{\#\Omega }$ for countable, discrete outcome spaces follow the above axiom.

For a random variable $X\sim f(h)$ where h is the height of some population, the probability that $a<X<b$ is the shaded area:

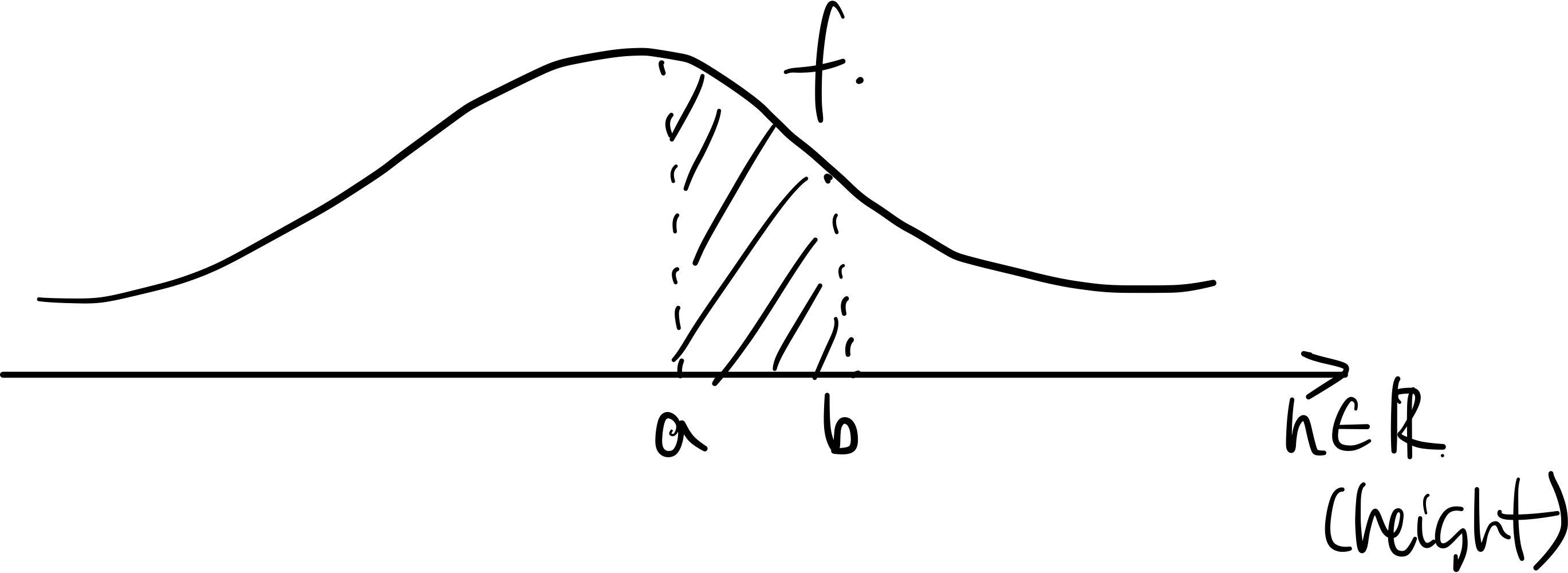
Calculated by: $P(a<X<b)={\int }_a^{b}f(h)dh$

Probability Mass Function §

def. Probability Mass Function. For a discrete random variable $X$, the probability mass function is the function that gies the probability of all values of $X$.

$$pmf(x)=\mathbb{P}(X=x)$$

thm. Addition Rule for Random Variables. For a discrete random variable $X,$ the following is true:

$$\mathbb{P}(a\le X\le b)=\sum _{k=a}^b\mathbb{P}(X=k)=\sum _{k=a}^{b}pmf(k)$$

Probability Density Function §

def. Probility Density Function. $f_X(x)$ is a probility density function of random variable $X$ iff:

1. $\forall x,f_X(x)\ge 0$
2. $\forall x,{\int }_{-\infty }^{\infty }{f}_X(x)dx=1$
3. $\mathbb{P}(a\le X\le b)={\int }_a^b{f}_X(x)dx$

def. Cumilitave Density Function. $F_X(t)$ is the cumulative density function of random variable $X$:

$$\begin{gathered} F_X(t):={\int }_{-\infty }^t{f}_X(x)dx \\ \equiv \mathbb{P}(X\le t) \end{gathered}$$

if and only if:

1. $\forall t,F_X(t)\ge 0$
2. $F_X(t)$ is never decreasing over its domain
3. ${\lim }_{t\to \infty }{F}_X(t)=1$

Info

Relationship between $f_X(x)$ and $F_X(x)$ is a derivate and antiderivative.

$$>f_X(x)\underset{\text{anti-derivative}}{\overset{\text{derivative}}{\leftrightharpoons }}{F}_X(x)>$$

Note that when you get $F_X(x)$ you will get a integration constant $C$. You can get rid of this by using the property ${\lim }_{t\to \infty }{F}_X(t)=1$.

• Joint Distributions
• Conditional Distribution

List of Common Distributions §

• Uniform Distribution
• Bernouilli Distribution
• Gamma Distribution
• Exponential Distribution
• Normal Distribution
• Student’s T-Distribution
• Poisson Distribution
• Binomial Distribution
• Multinomial Distribution
• Hypergeometric Distribution