Maximum Flow Problem

Q. Maximum Flow Problem. Given a Directed Graph whose edges are labeled with flow capacity, what is the maximum flow that can be pushed from vertex $s$ to $t$?

Q. Minimum Cut Problem. Given a Directed Graph whose edges are labeled with flow capacity, and a source and target vertex $s,t$, how do you partition the graph into $A,\bar{A}$ such that the flow capacity from $A\to \bar{A}$ is minimized?

⇒ The two questions give the same answer. i.e…

• the flow rate between $A\to \bar{A}$ is the maximum flow rate of the graph
• For the edges cut by the min-cut…
  • all forward edges operate at full capacity. (The sum of forward edges is the maximum flow capacity of the whole graph.)
  • all backward edges operate at zero capacity

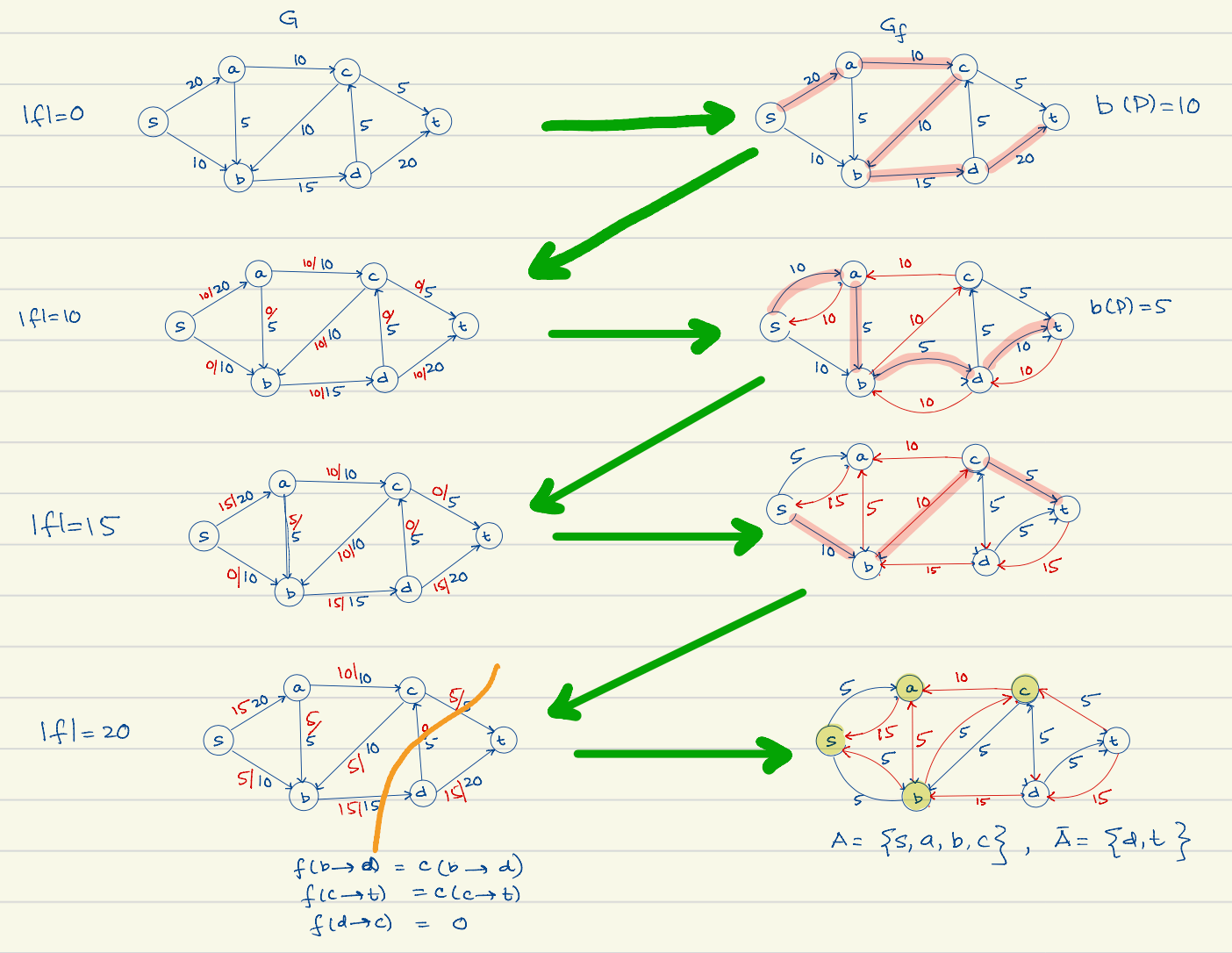
alg. Ford-Fulkerson Flow Maximization. (FFF-Max) Worked Example

• Idea: Choose some suboptimal flow, then increamentally find a better solution.

1. Choose some suboptimal flow through the graph.
2. Construct a residual network.
   1. For edges who have residual capacity, keep those edges but labeled with that residual capacity.
   2. For every edge, construct a reversed edge with the used capacity (this is useful later)
3. If there is still a path from $s\to t$ in the residual network, then more flow can be pushed.
   1. This path is called the ”flow augmenting path”
   2. The minimum capacity of any edge in the augmenting path is the ”bottleneck” of the path.
   3. ! Choice of the augmenting path is important. Discussed below.
   4. Rewire the original graph so that…
      1. forward edges have their flow decreased by the bottleneck amount
      2. backward edges—decrease flow of the forward edge represented by that backward edge by that bottleneck in the original graph
4. Repeat calculation until there is no path $s\to t$ in the residual graph.

alg. Minimum Cut. How to remove the minimum number of edges such that there is no flow from source $s$ to sync $t$?

1. Run the Flow Maximization algorithm
2. Construct a residual graph of the final max-flow graph.
3. From the source vertex, perform a search (DFS/BFS) and mark all reachable edges.
4. ⇒ The edges between reachable and unreachable verticies is the min-cut edges.

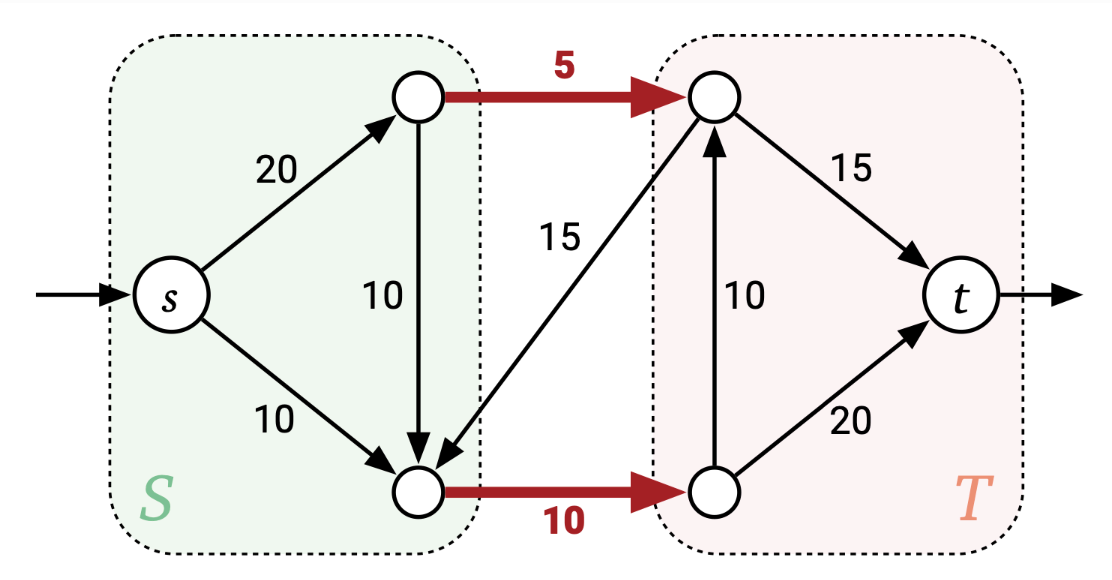
• Value of a cut is the sum of forward edges (=edges in the direction reachable → unreachable)
  • In case of a min-cut one needs to minimize this value
• Value of Min-cut $v$ is equal to the maximum flow $f$ thru the graph
  • (⇒) Given a min cut $s\to t$ and its value $v$, maximum flow thru $s\to t$ is $f\ge v$ because backward edges (15 is graph above) is
• A min-cut may not be unique
  • To find all of them, residual → run reachability → traverse cut edges to the nodes (may be multiple!)→ run reachability

alg. Choice of Augmenting Path. There are three common options:

• ! Assumptions:
  1. All capacities are integers
  2. $f^{\ast }$ is the ideal flow rate

1. Naive Method
   • Finding any path using BFS takes $O(E)$ time (fully connected graph)
   • Iteration count: $O(f^{\ast })$
   • Total: $O(E{f}^{\ast })$
2. Augmenting path with largest bottleneck.
   • Can use modified Shortest Path algorithm with $O(E\log V)$ time complexity
   • Iteration count: $O(E\log f^{\ast })$
   • Total: $O(E^2\log f^{\ast })$
3. BFS shortest augmenting path (Edmond-Karp)
   • Takes $O(E)$
   • Iteration count: $O(VE)$
   • Total: $O(V{E}^2)$
4. State of the art: $O(VE\log V)$, and even $O(E+ϵ)$

Discussion §

Formalization §

• the answer is given as a flow function $f:E\mapsto \mathbb{R}>0$.
  • i.e. “assign each edge a flow value”
• all vertices except the source and target vertices $s,t$ must have net zero divergence (=net zero inflow/outflow)
  • i.e. “the water can’t disappear or appear randomly in any vertex.”

Applied Problems §

k things with a separate set of l things, suspect flow/cut problem.

Q. Edge Matching Problem. (=Maximum Cardinality Matching) Given an undirected, partitioned graph, return the maximum number of edges that don’t share a vertex

• Idea: reduce to a max-flow problem.
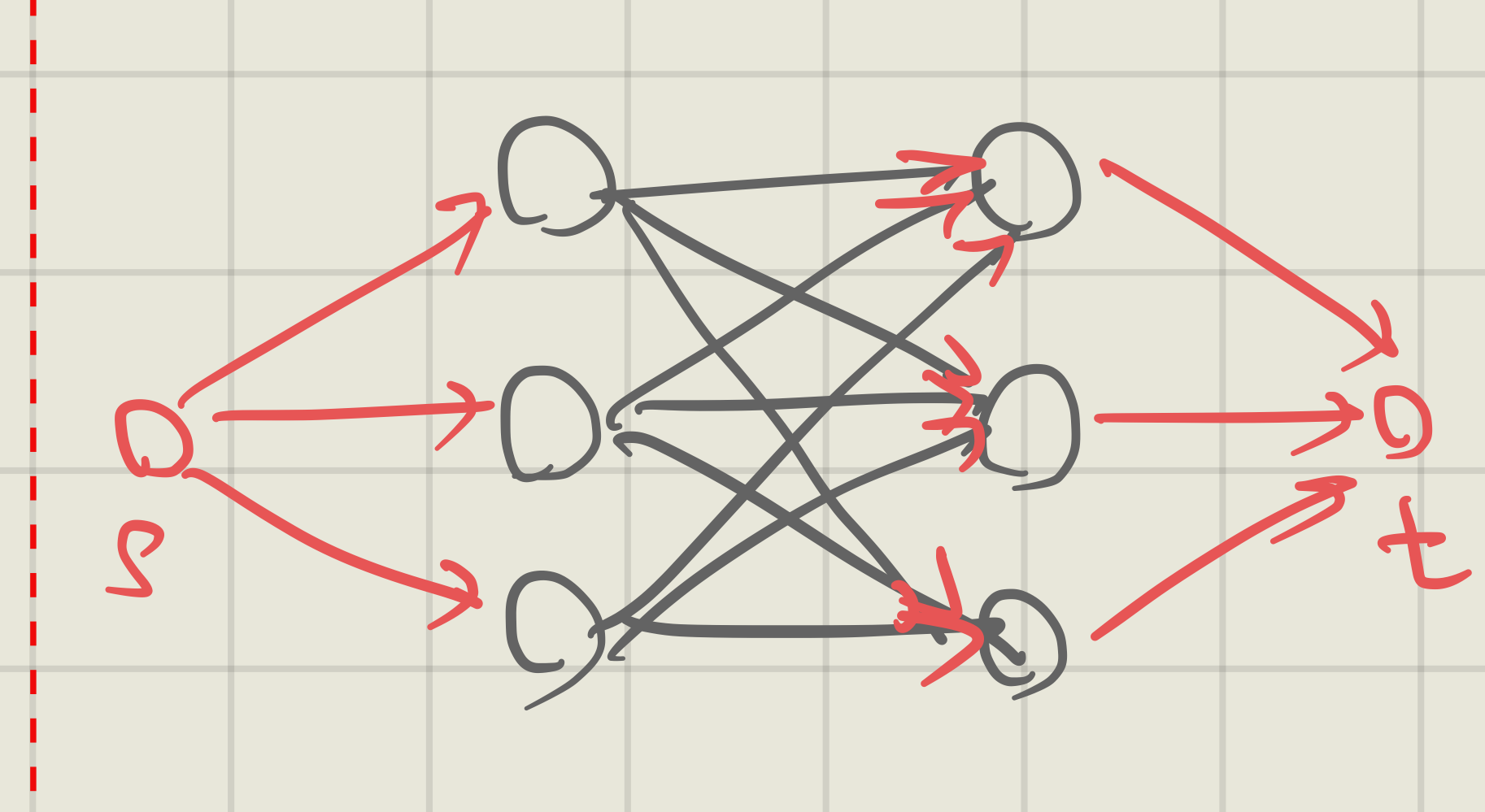
• algorithm:
  1. For a graph partitioned $A,B$, make all edges $A\to B$ directed.
  2. Construct start and end node $s,t$, and construct $s\to a\in A$, $t\leftarrow b\in B$
  3. Calculate the max-flow from $s\to t$
  4. The edges that are used in the max-flow problem is the solution.
• Complexity: $O(VE)$

Q. Advertiser and Viewer Demographic Matching Problem

Q.