Regression Discontinuity

Regression Discontinuity analysis is useful when

1. The assignment variable ($\approx$independent variable) is continuous (not binary)
   1. “Treatment” thus simply means after-cutoff
   2. We can’t just use Difference of Means because the assignment variable continuously changes in each groups too and thus affects the dependent variable too.
2. No other factors change when crossing the cutoff Then we can use the basic (constant-slopes) RD model:

$$Y_i={\beta }_0+{\beta }_1\underset{\text{ treatment var. }}{\underbrace{T_i}}+{\beta }_2\underset{\text{ assignment var. }}{\underbrace{(X_{1i}-C)}}+{ϵ}_i$$

where:

• $C$ is the cutoff point

• $T$ is $1$ for post-cutoff, $0$ for pre-cutoff. Simulates “treatment”

• $X_1$ is the assignment variable (non-adjusted). where coefficients mean:

• $\widehat{{\beta }_1}$ is the causality of treatment

• $\widehat{{\beta }_2}$ is the causality of the assignment var

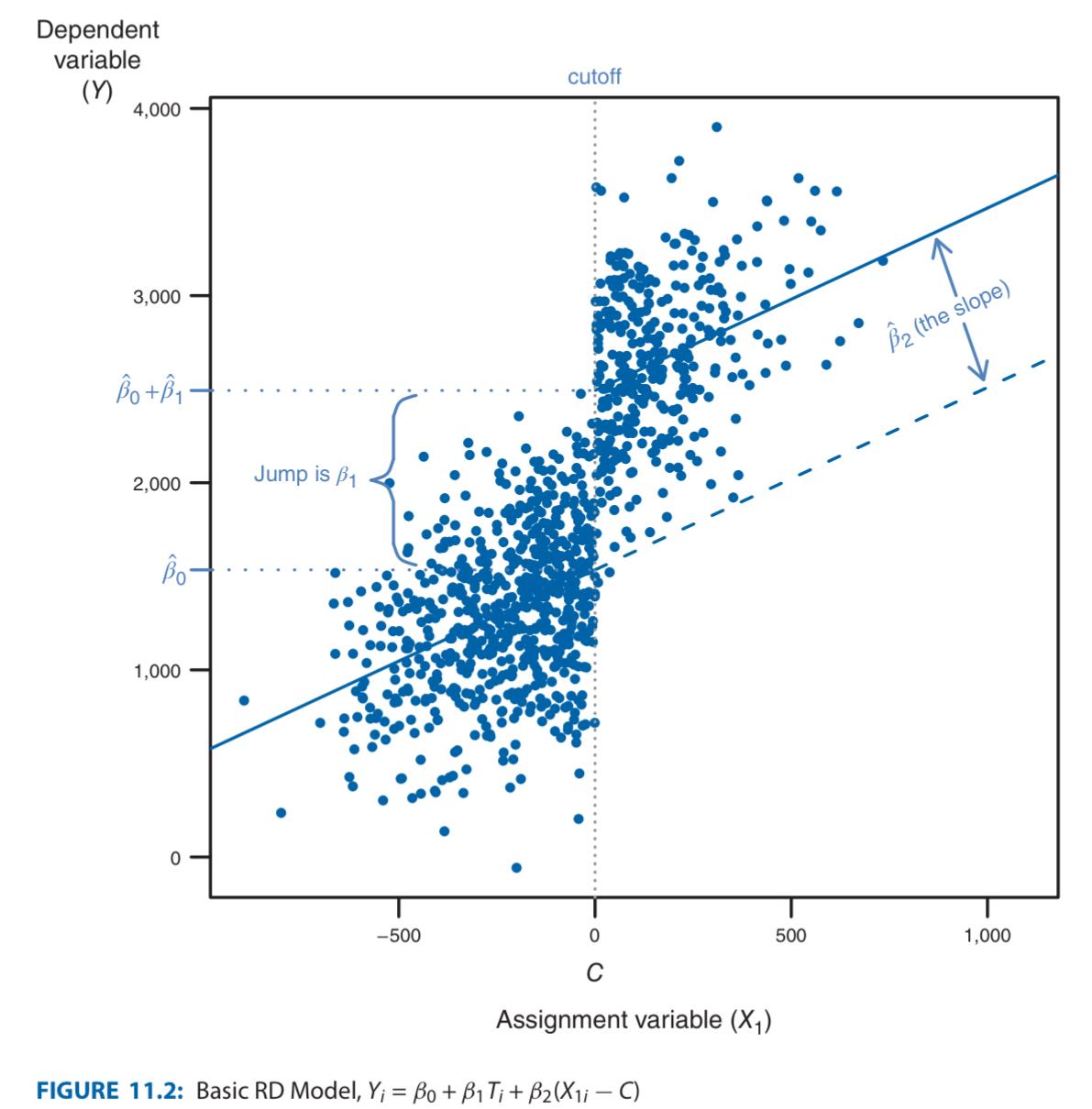
• Error term shouldn’t be jumping at the cutoff, i.e. we should have ${\rho }_{X_1,ϵ}=0$

  • If ${\rho }_{X_1,ϵ}\ne 0$ then $ϵ=\rho X_{1i}+{\nu }_i$ thus the basic RD model from above becomes:

$$Y_i={\beta }_0+{\beta }_1{T}_i+{\beta }_2(X_{1i}-C)+\rho X_{1i}+{\nu }_i$$

- → Thus even if $\rho_{X_{1},\epsilon}\neq 0$, $\hat{\beta_{1}}$ is unbiased (i.e. still correctly indicates the causality between treatment and $Y$)!
- But $\hat{\beta_{2}}$ no longer indicates causality between $X_{1}$ and $Y_{i}$, instead just indicates. overall correlation.

Advanced RD §

We don’t need to limit ourselves to have the slopes be same before and after discontinuity by using the varying slopes model:

$$Y_i=\stackrel{\text{ intercept after }}{\overbrace{\underset{\text{ intercept before }}{\underbrace{{\beta }_0}}+{\beta }_1{T}_i}}+\underset{\text{ slope before }}{\underbrace{{\beta }_2}}(X_{1i}-C)+\underset{\text{ slope after }}{\underbrace{{\beta }_3}}(X_{1i}-C)\times T_i+{ϵ}_i$$

Smaller windows → probably linear

Issues with RD Analysis §

• Smaller window (=bandwidth): We must look at variables close to the cutoff (because the farther away you go, the more endogenity there might be) But this isn’t always possible because of limited sample size.
• Probably only estimates the Local Average Treatment Effect (LATE), meaning that you can’t generalize the results. (“Are effects of drinking (vial legal age) on grades affect babies? old econometrics professors?“)
• Multiple variables usually determine treatment or not. (medicare and age is clear-cut; SAT and college admission isn’t) → use Fuzzy RD model
  • Or, we can use the Balace Test to see if the side of the cutoff is truly random
• Error term jumps at discontinuity (the issue from above)
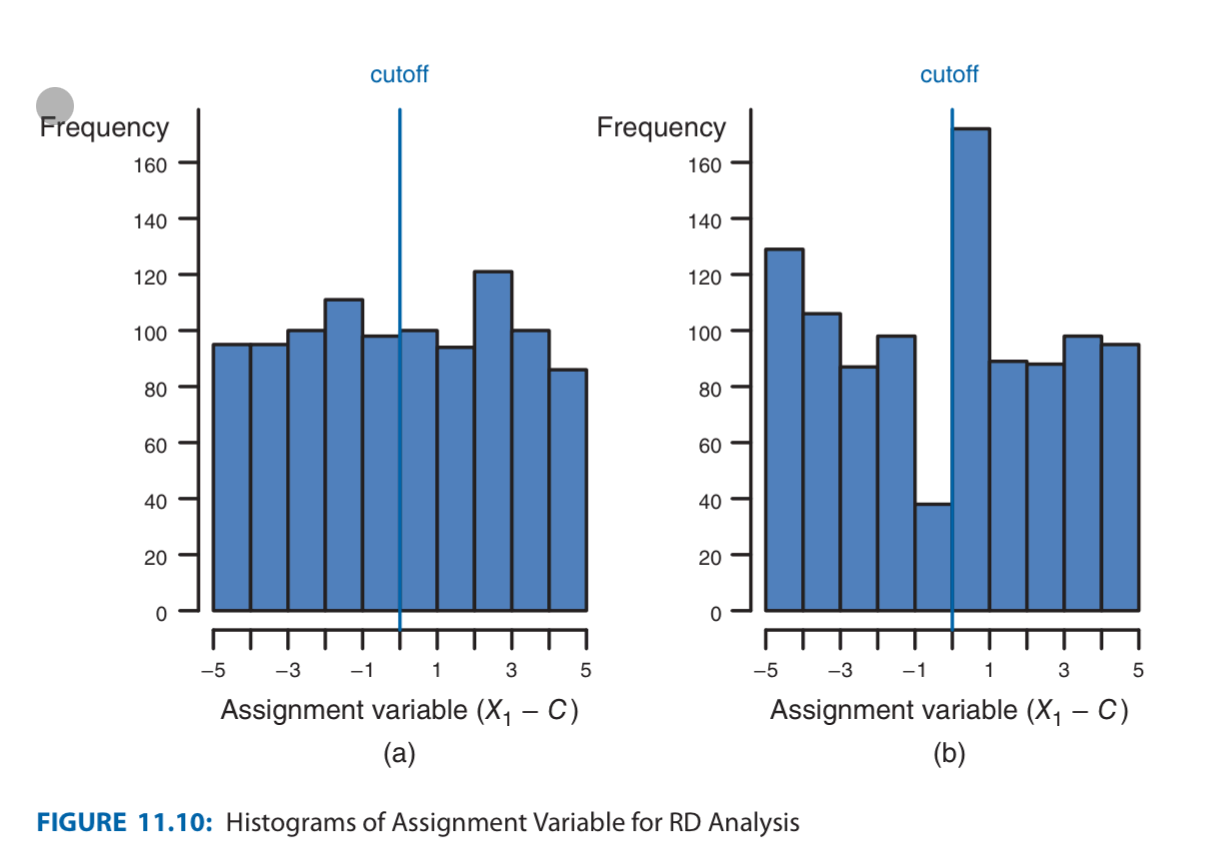
  • To check, make sure the frequency of the assignment variable is smooth at cutoff (e.g. the number of people (=samples) with SAT scores just below 1500 and just above 1500 isn’t too different from the rest of the grade.)
    • If there is, it might mean that people under 1500 wanted to get into colleges with cutoff score at 1500, so studied a little bit harder.
  • Visualization.
  • Another way to check this is to run regression between covariate (which we suspect to be in the error term) and the RD model: $X_{2i}={\gamma }_0+\underset{\text{ jump }}{\underbrace{{\gamma }_1}}{T}_i+{\gamma }_2(X_{1i}-C)+{\nu }_i$
    • A Statistically significant ${\gamma }_1$ indicates $X_2$ is in the error term