Variational Autoencoders

Motivation. Autoencoders have the problem of unstructured latent space, i.e. when sampling purely randomly in the latent space $\mathbf{h}$ and decoding it to $\mathbf{x}$, the generated data $\mathbf{x}$ is not very good—there are only a few ‘locations’ in the latent space that represents realistic data. To solve this, we must ‘structure’ the latent space such that sampling it would almost always give real data. The simplest idea would be to force the latent space to be a standard normal distribution.

def. Variational Autoencoder (VAE).¹² Let a probability distribution of data $p(\mathbf{x})$ and latent distribution of $p(z)=\mathcal{N}(0,1)$.

1. The encoder encodes the data into variables $\mu ,\Sigma$. This forms the conditional latent distribution, $p(\mathbf{z}|{\mathbf{x}}^{\text{observed}})=\mathcal{N}(\mu ,\Sigma )$.
   • Note that the latent representation is not a vector like autoencoders, but instead a full probability distribution
2. The decoder then takes a sampled latent point ${\mathbf{z}}^{\text{realized}}$, and decodes it into the datapoint to get a distribution for the data 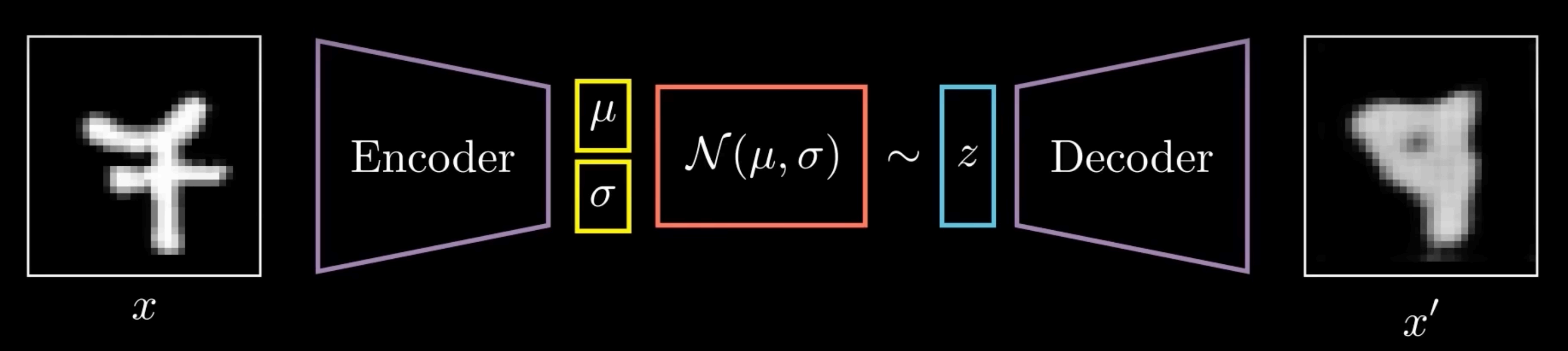$p(\mathbf{x}|{\mathbf{z}}^{\text{realized}})$. Objective. The loss, also known as Evidence Lower Bound (ELBO) can be shown to be as follows:

$$\mathcal{L}()=\stackrel{\text{ L2 Norm }}{\overbrace{{\mathbb{E}}_{q(z|x)}[\ln p(x|z)]}}-\underset{\text{ Make sure it becomes std. norm. }}{\underbrace{D_{\text{KL}}[\stackrel{\mathcal{N}({\mu }_q,{\Sigma }_q)}{\overbrace{q(z|x)}}\Vert \stackrel{\mathcal{N}(0,1)}{\overbrace{p(z)}}]}}$$

where the terms: 3. Expectation term is equivalent to the L2 Norm between the original image ${\mathbf{x}}^{\text{observed}}$ and the reconstruction ${\mathbf{x}}^{\text{reconstructed}}\sim p(\mathbf{x}|{\mathbf{z}}^{\text{realized}})$ 4. KL-divergence term is simply to make sure that $q(\mathbf{z}|\mathbf{x})$ resembles a standard normal distribution.

Footnotes §

1. Variational Autoencoders | Generative AI Animated - YouTube ↩

2. Variational AutoEncoders (VAE) with PyTorch - Alexander Van de Kleut ↩