Common Graph Problems

See also:

• Traveling Salesperson Problem
• Minimal Spanning Tree Problem

Q. Clique Problem. Given a graph $G=(V,E)$ what is the maximum set of vertices $C$ such that all vertices $v$ in $C$ are fully connected, i.e. for every $u,v\in C$, there exists edge $(u,v)\in E$

• NP-complete problem

Q. Independent Set Problem. (=Stable set =anti-clique) Given a graph $G=(V,E)$ what is the maximum set of vertices $C$ such that no edges connect any two vertices in this set?

• Complement with vertex cover.
  • $C$ is an maximal independent set ⇔ $V-C$ is a minimal vertex cover
  • Reduction both ways is trivial thm. 3-SAT ${\le }_p$ Independent Set
  1. Construction: each clause to a fully connected tri-vertex component, and connect the variable and its negations between tri-vertex components.
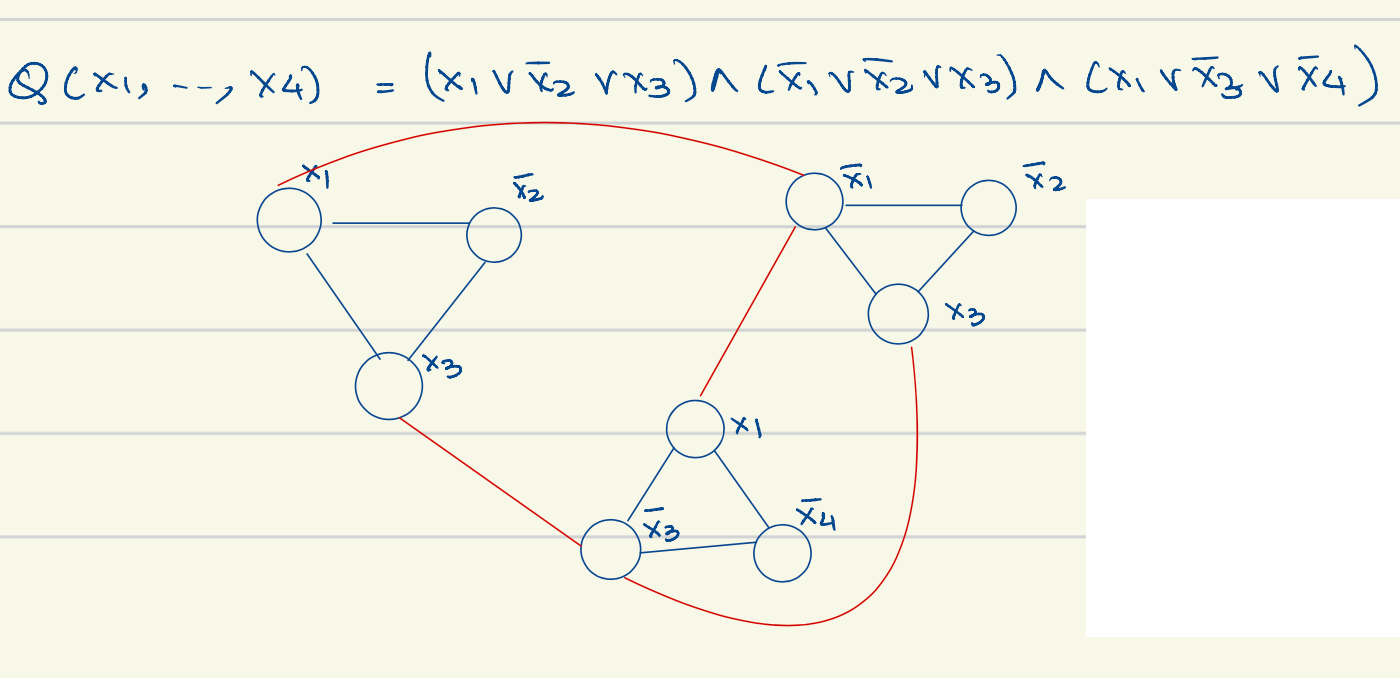
  2. $\exists x_1\dots x_n$ that satisfies $Q$ where $Q$ has $k$ clauses ⇔ $\exists$ Independent Set of size $k$.

Q. Vertex Cover. Given $G=(V,E)$ find the minimal subset $C\subseteq V$ such that it covers all edges in the graph.

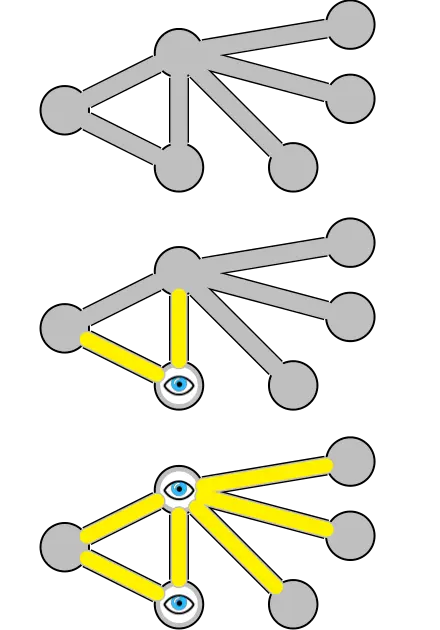
• e.g. graph that has a vertex cover comprising 2 vertices (bottom), but none with fewer.
• NP-complete problem
• $C$ is a minimal vertex cover ⇔ $V-C$ is a maximal Independent Set
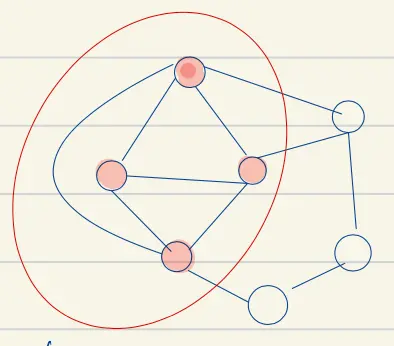
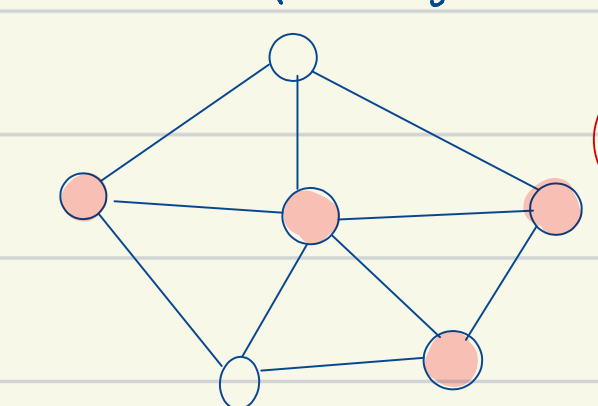
  • Red is vertex cover, and white is independent set:

alg. Approximate Vertex Cover.

1. Choose any edge $e$ that connects vertices $u,v$
2. remove edge $e$ from graph, as well as any edges that connected to $u$ and $v$
   1. $u,v$ are added to the vertex cover set
3. Repeat until no edges remain

• Is a 2-approximation

alg. Approximate Greedy Vertex Cover.

1. Choose vertex with maximum degree
2. Add this as part of vertex cover. Remove edges connected to this vertex
3. Repeat until no edges remain

• Is not optimal.

Q. Triangle Cover. Given $G=(V,E)$ find the minial subset of vertices that it covers at least one vertex per triangle, for every triangle in graph.

• Triangle Cover is NP-complete (reduce from vertex cover)

Q. Dominating Set. Given $G=(V,E)$ find the minial subset $S$ of vertices such that, every vertex in $G$ is either in $S$ or is a neighbor of $S$

Q. Critical Vertices. Given connected graph $G=(V,E)$ find all vertices that when removed will disconnect the graph.