Fixed Effects Model for Panel Data

Panel data is a dataset that have multiple observation on a same timeframe. e.g.:

• GDP of OECD countries from 1900 to 2000
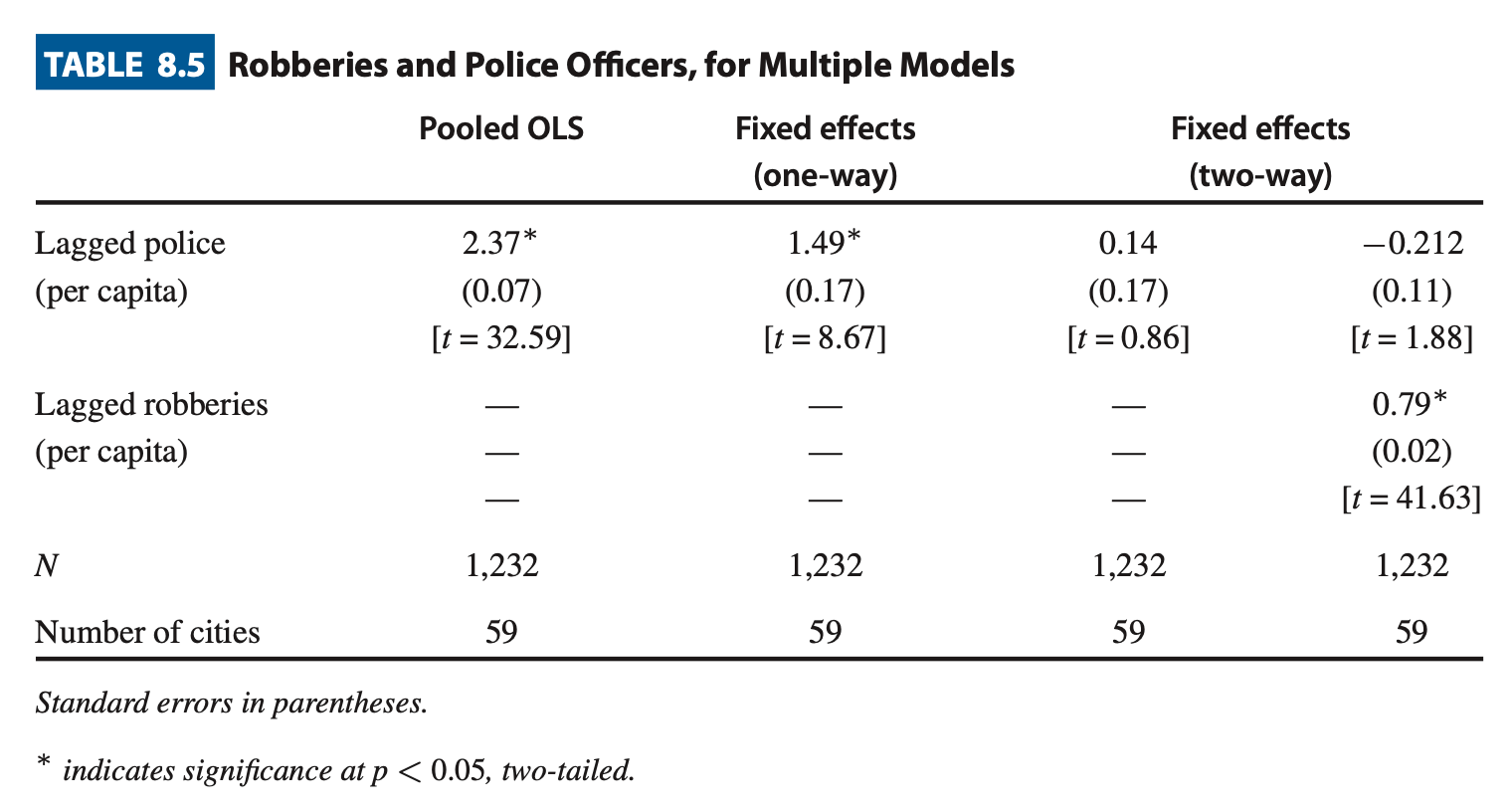
• Annual crime rates of 20 U.S. Cities from 1980 to 2000 Pooled Model is when we mistakenly use all of the panel data to run the regression. Exmaple. Robberies for large cities of California. Each city has its own reasons for having relatively larger or smaller robberies unrelated to policing. You can see that there are general clumps of datapoints corresponding to cities. 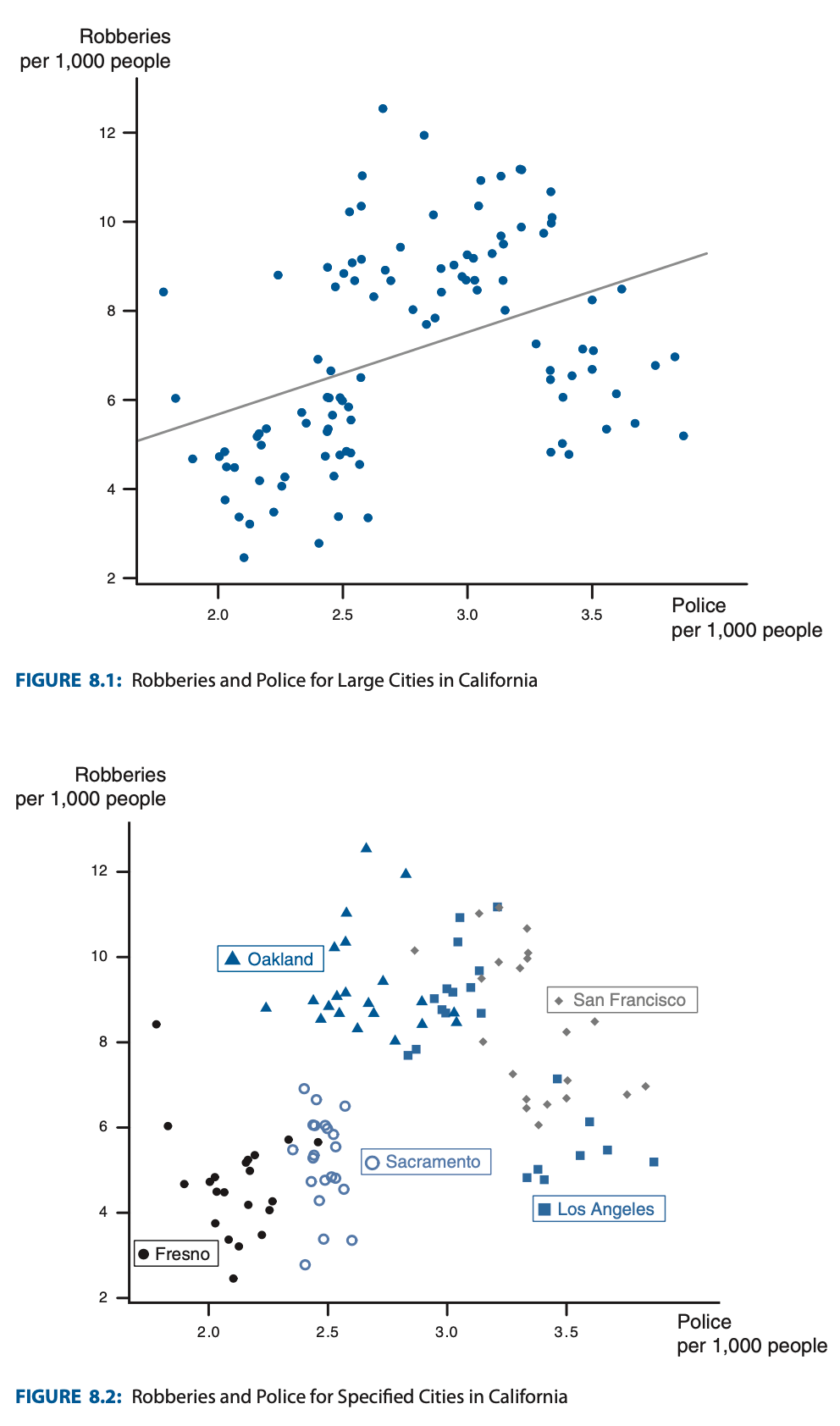Instead, we should separate the dataset w.r.t. cities and run regression on each of them separately: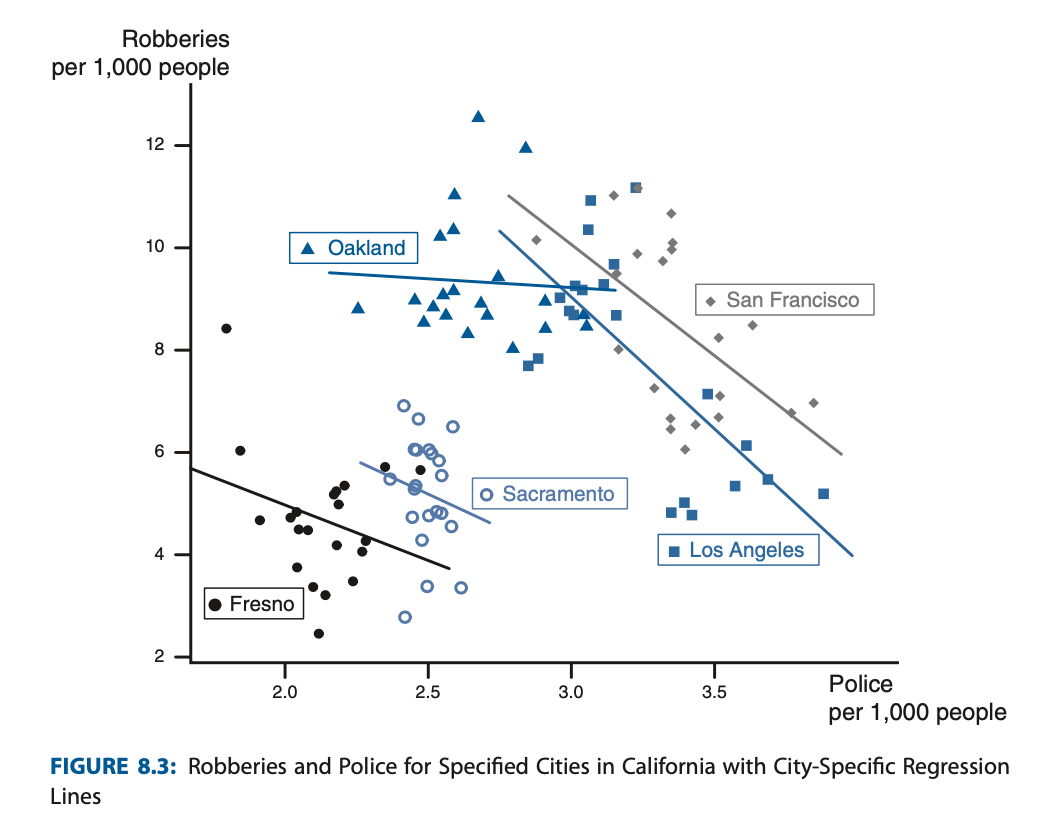

One-way Fixed Effects Model §

Motivation. In order to use a single regression run to capture the difference in cities, we introduce a fixed effect term (${\alpha }_i$), a addtitive term that is same for each city (i.e., all oakland datapoints have the same ${\alpha }_i$, all SF datapoints have the same ${\alpha }_i$, etc.). The model is this:

$$Y_{it}={\beta }_0+{\beta }_1{X}_{1it}+\underset{\text{ fixed effect }}{\underbrace{{\alpha }_i}}+\underset{\text{ error }}{\underbrace{{\nu }_{it}}}$$

• $i$ indexes on each city
• $t$ indexes on year (time) We can’t run regression on this directly because we don’t know what we should set ${\alpha }_i$ as. We instead use either Dummy Variables approach or a De-meaned apporach. Both result in the exact same regression result.

Least-Squares Dummy Variable Fixed Effects Model (LSDV) §

$$Y_{it}={\beta }_0+{\beta }_1{X}_{1it}+{\beta }_2{D}_{1i}+\cdots +{\beta }_P{D}_{P-1,i}+{\nu }_{it}$$

Where $D_{1i},\dots ,D_{P-1,i}$ are the binary dummy variables. We run regression on this to get the regression table:

De-Meaned Fixed Effects Model §

$$Y_{it}-{\bar{Y}}_i={\beta }_1(X_{it}-{\bar{X}}_i)+{\tilde{\nu }}_{it}$$

By subtracting the mean of each group from the datapoints, we “normalize” the data so that they’re all comparable.

Discussion §

• Fixed effects models cannot cause bias when used in non-panel data (i.e. all ${\alpha }_i=0$)
• When ${\alpha }_i\ne 0$, and we use a pooled model, it only causes bias when fixed effect is correlated with independent variable (=${\alpha }_i$ and $X_{1i}$) are correlated

Two-way Fixed effects model §

Motivation. We may want to control for time period, e.g. for 2008 during the financial crisis, crimes in all cities probabily went up. The two-way model controls for time-based fixed effects too in our Califorinan crimes example, with the following model:

$$Y_{it}={\beta }_0+{\beta }_1{X}_{1i}+\underset{\text{ city fixed eff. }}{\underbrace{{\alpha }_i}}+\underset{\text{ time fixed eff. }}{\underbrace{{\tau }_t}}+{\nu }_{it}$$

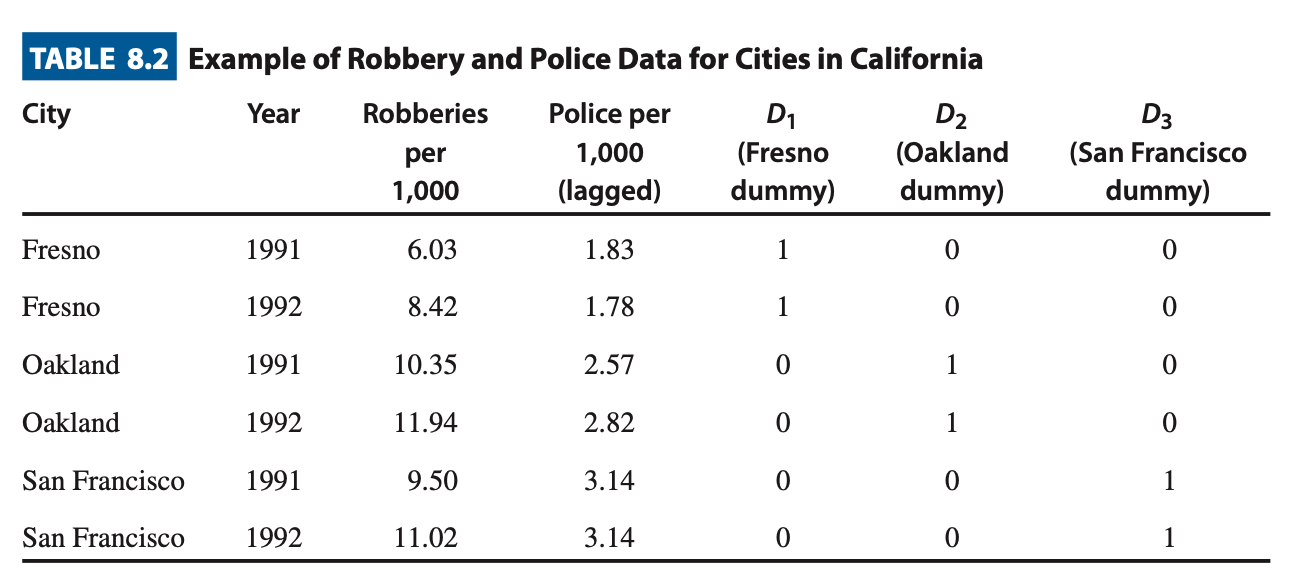
We can use double-LSDV, doubkle De-meaned, or LSDV-De-meaned approach. This is not discussed in the book. Comparing the regression results for pooled, one-way, and two-way: