Database Design Theory

How to reduce a Relational Model to make it more compact.

Armstrong’s Axioms §

• Reflexivity: $Y\subseteq X⟹X\to Y$
• Augmentation: $X\to Y⟹XZ\to YZ$
• Transitivity: $X\to Y\text{ and }Y\to Z⟹X\to Z$

Secondary Rules §

• Decomposition: $X\to YZ⟹X\to Y,X\to Z$
• Composition: $A\to B,X\to Y⟹AX\to BY$
• Union: $X\to Y,X\to Z⟹X\to YZ$
• Pseudo-transitivity: $X\to Y,YA\to Z⟹XA\to Z$
• Identity: $X\to X$
• Extensivity: $X\to Y⟹X\to XY$

Functional Dependency §

def. Functional Dependency. If for all tuples in a relation that has the same values for attribute $X$ and attribute $Y$, then $Y$ is functionally dependent on $X$.

$$\exists f:X\mapsto Y⟹X\to Y\text{...read "Y Depends on X"}$$

e.g. an address relation with street, city, state, zip

• zip → (city, state)
  • Zip code determines city and state
• (zip, state) → zip
  • This is a Trivial dependency:= $RLHS\supseteq RHS$
• zip → (state,zip)
  • This is non-trivial, but not complete,
  • Complete Non-trivial dependency:= $LHS\cap RHS\ne \varnothing$

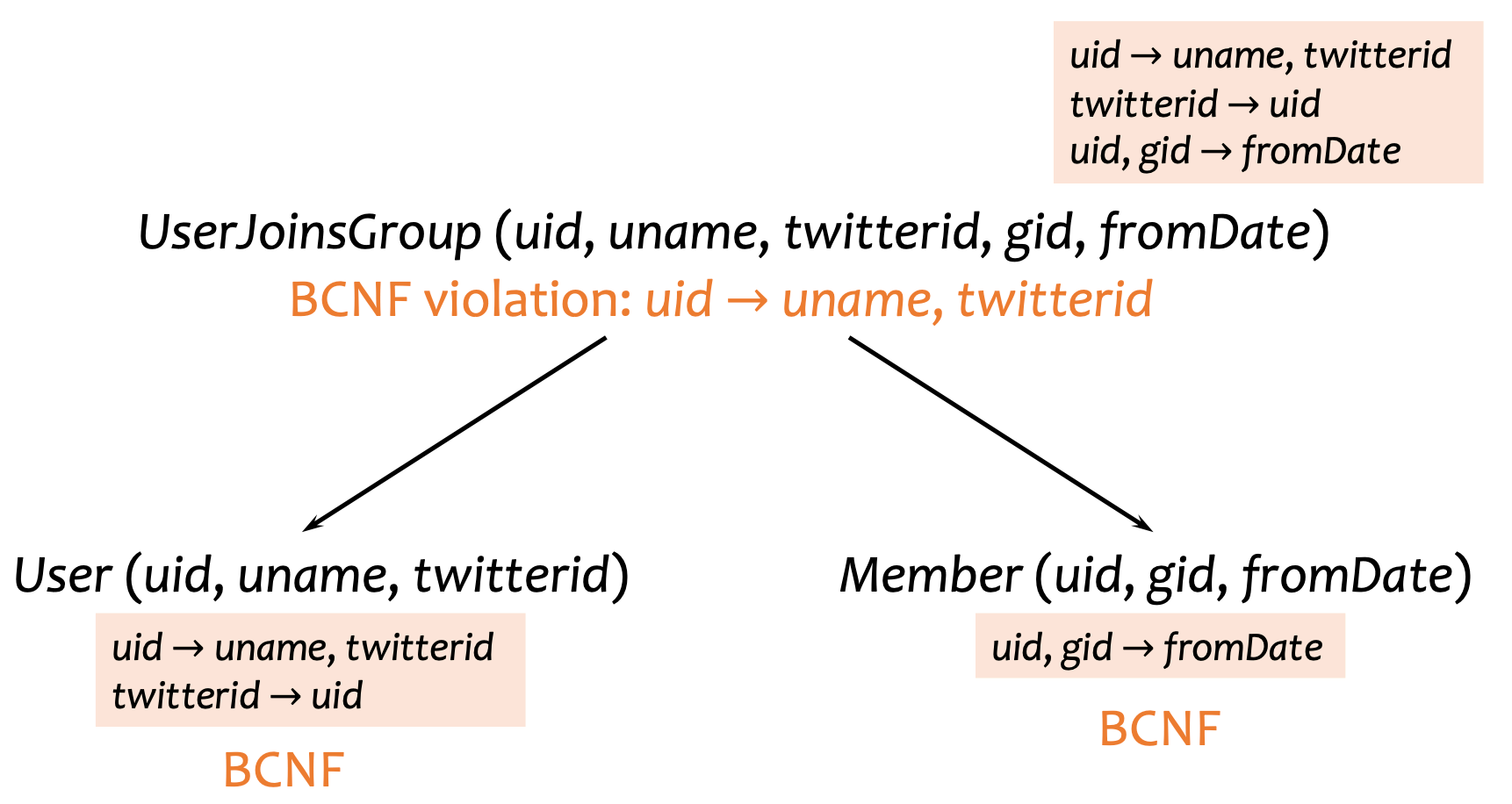
alg. BCNF decomposition procedure. Given a set of dependencies $\mathcal{F}$ and relation $R$, BCNF decomposition determines a minimally redundant (=row-redundant) Relation.

1. Choose (non-determinisitcally) a dependency in $\mathcal{F}$, let $X\to Y$ which is non-trivial (=$X$ is not a superkey)
2. Decompose using $X$ into two relations $R_1,R_2$
   • $R_1$ has attributes $X\cup Y$
   • $R_2$ has attributes $X\cup (attr(R)-Y)$
3. Recurse procedure for $R_1,R_2$

• It’s a non-deterministic process (=there can be multiple ways to decompose a relation). def. Closure. Given dependencies $\mathcal{F}$, the closure $Z^{\ast }$ of set of attributes $Z$ is all attributes determined by $Z$ through those dependencies

Finding a Key Using Functional Dependencies §

alg. Given set of functional dependencies $\mathcal{F}$ on relation $R$, find the keys of the schema

1. For each dependencies $LHS\to RHS$, compute the closure of $LHS$ such that $LHS\to LH{S}^{\ast }$.
   1. If $LH{S}^{\ast }$ doesn’t contain all the attributes of $R$, then augment $LHS$ such that it reaches all the attributes.
      1. i.e., let $\text{Remain}=attr(R)-LH{S}^{\ast }$
      2. then, it must be $LHS\cup \text{Remain}\to attr(R)$
   2. Then, $LHS\cup \text{Remain}$ is a superkey of $R$. let this be $S$.
   3. Can you reduce this superkey $S$?
      1. Try taking out one attribute at a time from $S$ to create $S^{\prime }$
      2. Is $S^{\prime }$ reducible?
      3. → Repeat until we reach something unreducible.
      4. ⇒ The final $S^{\prime }$ that is unreducible is a key.
2. Repeat for all dependencies in $\mathcal{F}$.

Multi-value Dependency §

def. Multi-value Dependency (MVD). $Y$ is a multi-value dependency of $X$ if…

• for all tuples with the same values of $X$…
• …if we swapped all the $Y$ values of them…
• …those entries also exist in the database. then:

$$X\twoheadrightarrow Y$$

In colloquial terms, we can say that for every determined value of $X$, all tuples with values of $Y$ “associated” with that $X$ must exist too. def. Trivial MVD. Given relation $R(A,B,C)$:

• $A,B\twoheadrightarrow C$: Obvious. $LHS\cup RHS=attrs(R)$
• $A,B\twoheadrightarrow A$: Obvious. $LHS\supseteq RHS$

def. 4th Normal Form (4NF). if every MVD in relation $R$ is $X\twoheadrightarrow Y$ such that $X$ is always a superkey, then relation $R$ is in the 4th Normal Form. Example

Multivalue Dependency Rules §

• Complementation: $X\twoheadrightarrow Y⟹X\twoheadrightarrow attrs(R)-X-Y$
• Augmentation: $X\twoheadrightarrow Y,B\subseteq A⟹XA\twoheadrightarrow YB$
• Transitivity: $X\twoheadrightarrow Y,Y\twoheadrightarrow Z⟹X\twoheadrightarrow Z-Y$
  • Automatically means $X\twoheadrightarrow Y,Y\twoheadrightarrow Z⟹X\twoheadrightarrow Z$
• Replication: $X\to Y⟹X\twoheadrightarrow Y$
• Coalescence: If 𝑋 ↠ 𝑌 and 𝑍 ⊆ 𝑌 and there is some 𝑊 disjoint from 𝑌 such that 𝑊 → 𝑍, then 𝑋 → 𝑍

Chase §

Proving theorems about chase. Example: alg. Tuple Generation. To enforce $X\twoheadrightarrow Y$ on table $R$

1. For a determined $X=x_i$
   1. Enumerate all availble $Y=y_1,y_2,\dots ,y_{?}$
   2. Enumerate all available
      1. let $Q:=attr(R)-X-Y$
      2. Enumerate all availalbe $Q=q_1,\dots ,q_{?}$
   3. Are all combinations $Y\times Q$ available in the table?
      1. If not, add missing ones
2. For another determined $X=x_2$, repeat
3. Repeat for all $X=x_1\dots x_{?}$

alg. Chase. To prove $X\twoheadrightarrow Y$…

1. Initialization: add two tuples $(x,y_1,\dots ),(x,y_2,\dots )$ to the initial table
2. For each MVD (order doesn’t matter):
   1. Tuple Generation: see above
3. For each FD (order doesn’t matter):
   1. You may infer equalities, e.g. $e_1=e_2$
4. Does $X\twoheadrightarrow Y$ fully available? (=$Y\times \text{Remaining Attrs}$ all in table)?
   1. Yes → proven
   2. No → disproven (counterexample)