Utility Maximization

$$\text{max}u(x_1,x_2)\text{such that}I=p_1{x}_1+p_2{x}_2$$

Maximization of the Utility Function against the Budget Constraints.

• Uses Lagrangian Optimization
• & If it makes it more convenient, do a Monotonic Transformation of the utility function. See Example.
• Optimal is where the budget line is the tangent to the Indifference Curve. This implies both gradients are same, i.e. $-\frac{P_1}{P_2}=MRS$
• The result is the Ordinary Demand functions (one for each good)
• See Expenditure Minimization for the opposite case
• ! Always check if the resulting $x_1,x_2$ are positive. If not, it’s piecewise function to keep both positive.

Perfect Substitutes §

With the form: $u=(a{x_1}^k+b{x_2}^l{)}^{\alpha }$

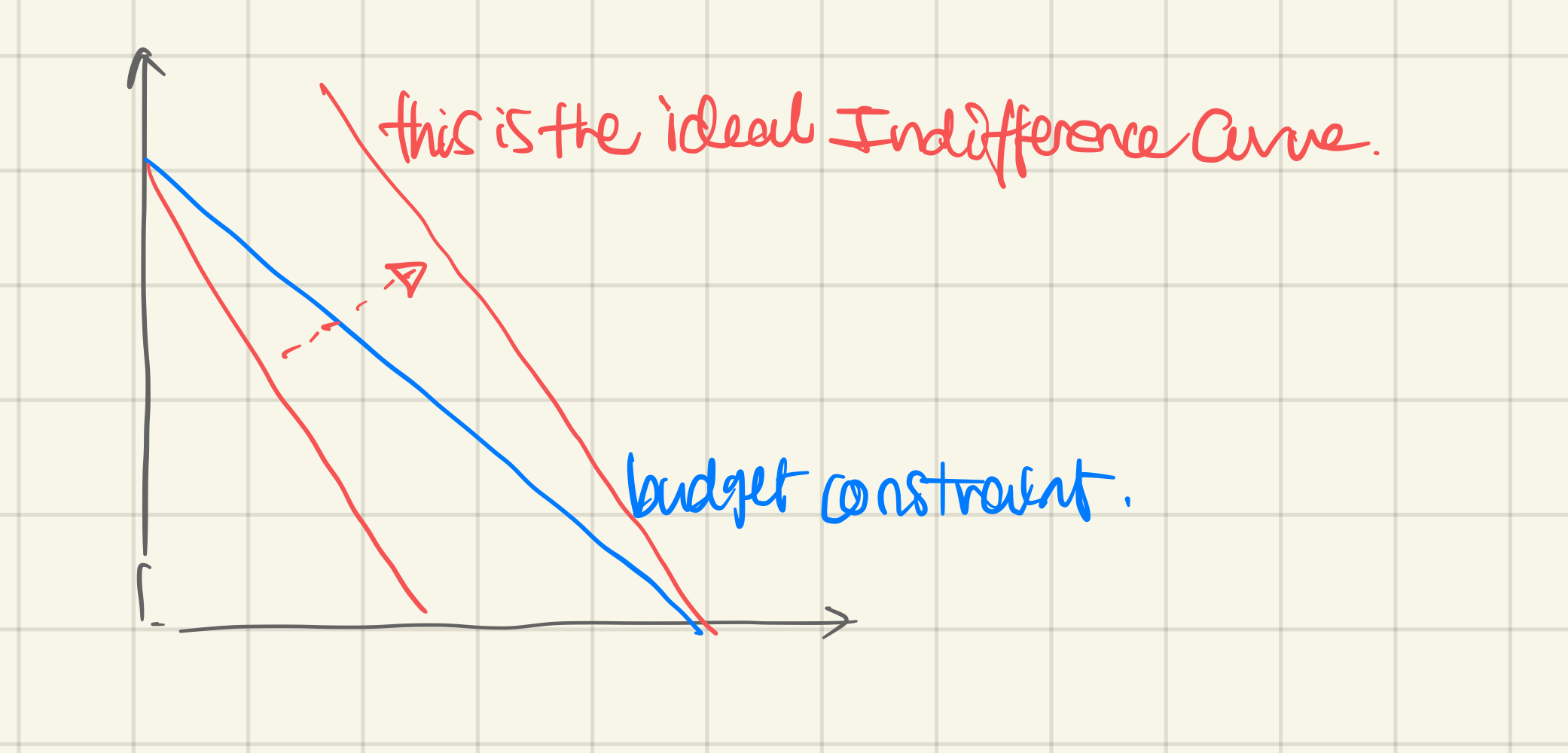⇒ Go to the corner that gives the highest utility (=buy only one good!)

$$x_1=\{\begin{array}{ll}\frac{I}{p_1}& \text{if }u\left(\frac{I}{p_1},0\right)\ge u\left(\frac{I}{p_2},0\right)\\ 0& \text{else}\end{array},x_2=\{\begin{array}{ll}\frac{I}{p_2}& \text{if }u\left(0,\frac{I}{p_2}\right)\ge u\left(0,\frac{I}{p_1}\right)\\ 0& \text{else}\end{array}$$

Perfect Compliments §

$${\text{max}}_{x_1,x_2}u(x_1,x_2)=min(x_1,2x_2)\text{ such that }I=p_1{x}_1+p_2{x}_2$$

1. Get the formula that is the set of all kinked points in the utility function ⇒ $x_1=2x_2$
2. Get the Constraint formula ⇒ $I=p_1{x}_1+p_2{x}_2$
3. Solve for the two equations (=get the intersection)

$$x_1=\frac{I}{2p_1+p_2},x_2=\frac{2I}{2p_1+p_2}$$

Quasilinear Optimization §

Use Lagrangian optimization, but beware that the blue line might happen (=maximum point lies outside 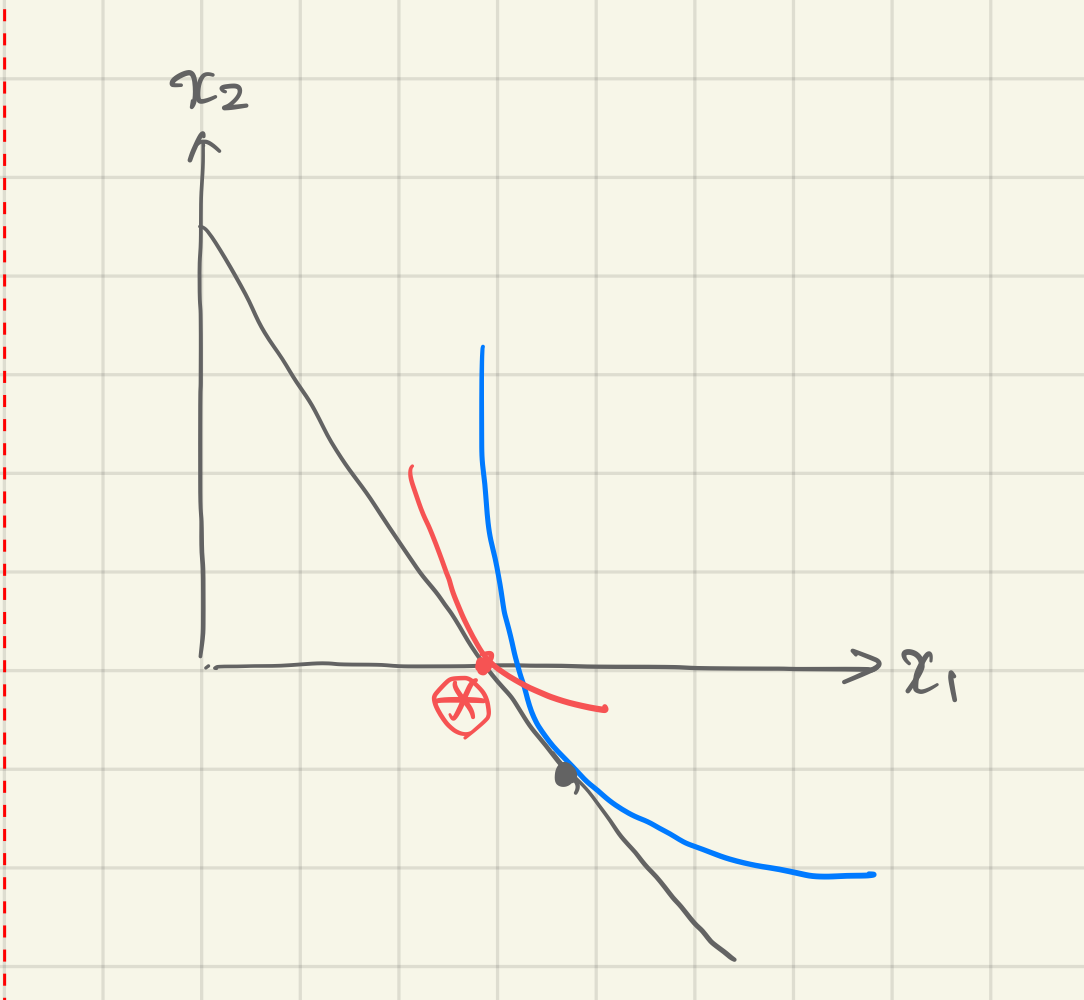$x_1,x_2>0$): ⇒ In this case, go to the red (*) corner solution.

Kinked Budget Constraint §

1. Case 1: Inner kink
   1. Lagrangian for blue section
   2. Lagrangian for red section
   3. Choose the better one
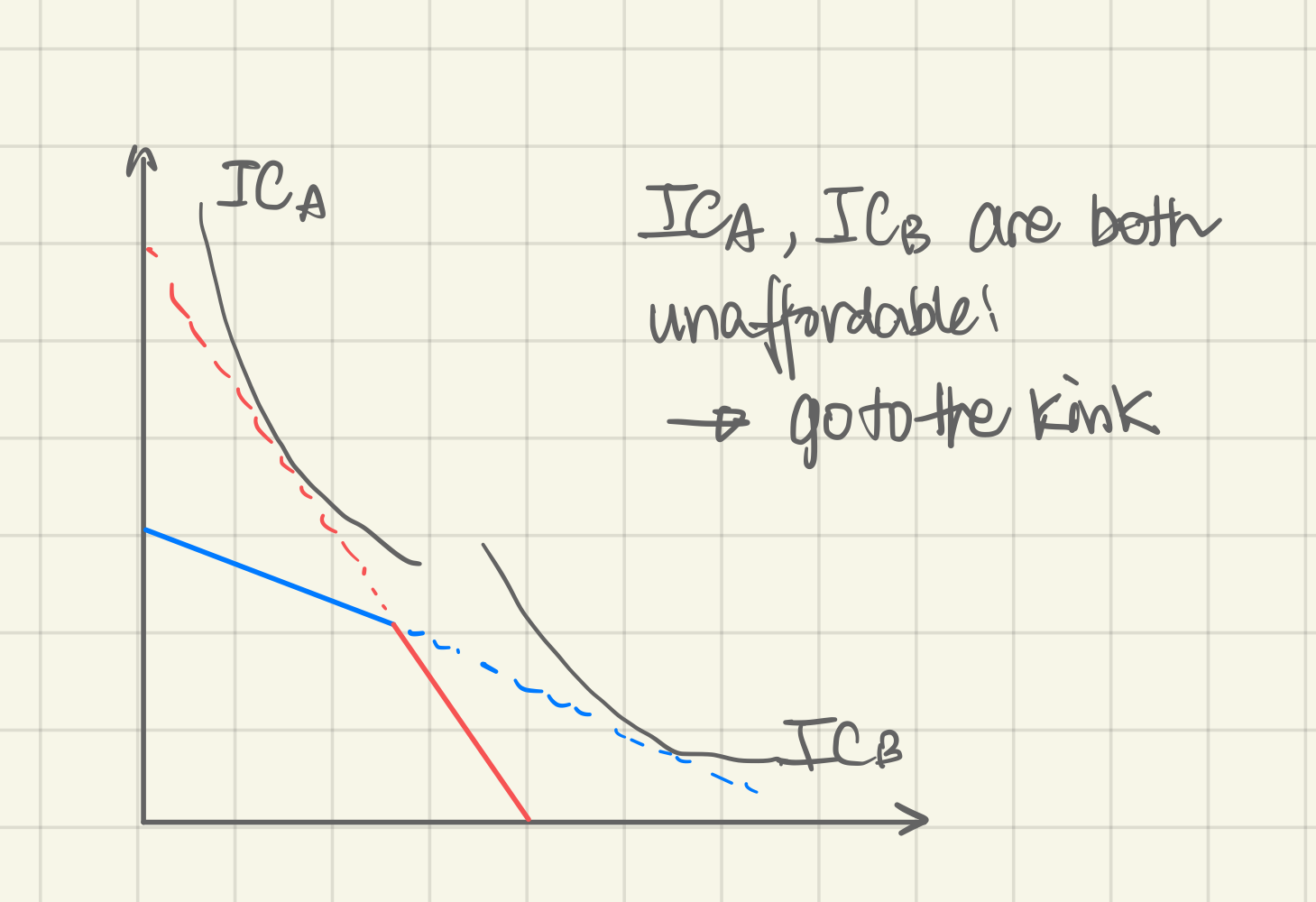
2. Case 2: Outer Kink
   1. Lagrangian for blue and red section
   2. If both solutions are unaffordable (=$I{C}_A,I{C}_B$ in the graph i.e. $x_2<0$ in graph,), go to the kink.

More than Two Goods §

1. Case 1: $u(x_1,x_2,x_3)=x_1^{\alpha }{x}_2^{\beta }{x}_3^{1-\alpha -\beta }$ ← Pure three-var cobb-douglas
   • ⇒ Use 3-var lagrangian
2. ==Case 2: $u(x_1,x_2,x_3)=x_1^{\alpha }{x}_2^{1-\alpha }+x_3$==
   1. Check that each term is Homogenous Degree of 1.
   2. Try the two-var lagrangian on the first term $x_1^{\alpha }{x}_2^{1-\alpha }$ (assumping $x_3$ isn’t consumed)
   3. Try to maximize $x_3$ (assuming $x_1,x_2$ isn’t used)
   4. Choose the higher of the two utilities
      • If there is no concrete number, the cases differ on the conditions $u(x_1,x_2,0)\lessgtr u(0,0,x_3)$

Solution for Case 2:

$${\text{max}}_{x_1,x_2,x_3}u=x_1^{\alpha }{x}_2^{1-\alpha }+x_3\text{ such that }I=p_1{x}_1+p_2{x}_2$$ $$\{\begin{array}{ll}\{\begin{array}{l}{x}_1=\frac{\alpha I}{p_1}\\ x_2=\frac{1-\alpha I}{p_2}\end{array}& \text{If }\frac{{\alpha }^{\alpha }(1-\alpha {)}^{1-\alpha }}{p_1^{\alpha }{p}_2^{1-\alpha }}\ge \frac{1}{p_3}\\ x_1=x_2=0\text{ and max}{x}_3& \text{Otherwise}\end{array}$$

Graphing a budget line with an indifference map, we can see that the bundle $B_1$ is where the consumer can achieve the most possible utility; where what is affordable = most possible utility

To find the bundle(=point) of maximum utility that is affordable, you can rephrase the problem as…

Worked Example: Constrained Optimization Problem §

Using the Lagrange Method for $\text{max }u(x_1,x_2)\text{ s.t. (budget line)}$,

$$\begin{gathered} \nabla u(x_1,x_2)=\lambda \nabla (p_1{x}_1+p_2{x}_2) \\ {p}_1{x}_1+p_2{x}_2=I \end{gathered}$$

To simplify further: $\nabla u(x_1,x_2)=\lambda \nabla (p_1{x}_1+p_2{x}_2-I)$ and thus let:

$$L=\nabla u(x_1,x_2)-\lambda \nabla (p_1{x}_1+p_2{x}_2-I)$$

to construct a set of equations where:

$$\begin{gathered} \frac{\delta L}{\delta x_1}=0 \\ \frac{\delta L}{\delta x_2}=0 \\ {p}_1{x}_1+p_2{x}_2=I \end{gathered}$$

and solve the three equations. Note that the Lagrange method doesn’t work when:

• One or more goods are non-essential, meaning that the budget line crosses the axes → It’s a corner solution; i.e. the maximum point is at one of the intercepts, or at points where quantities of goods are negative
• Tastes are non-convex, where there will be multiple solutions
• Utility Function are kinked or otherwise non-differentiable