Online Matching

Motivation. Suppose you are Google. Many advertisers come to you and want to advertise on google searches by users. Now, users come it throughout the day, one by one, searching for whatever they want to search. You can show them one advertisement. How do you maximize the advertisement to show to the users?

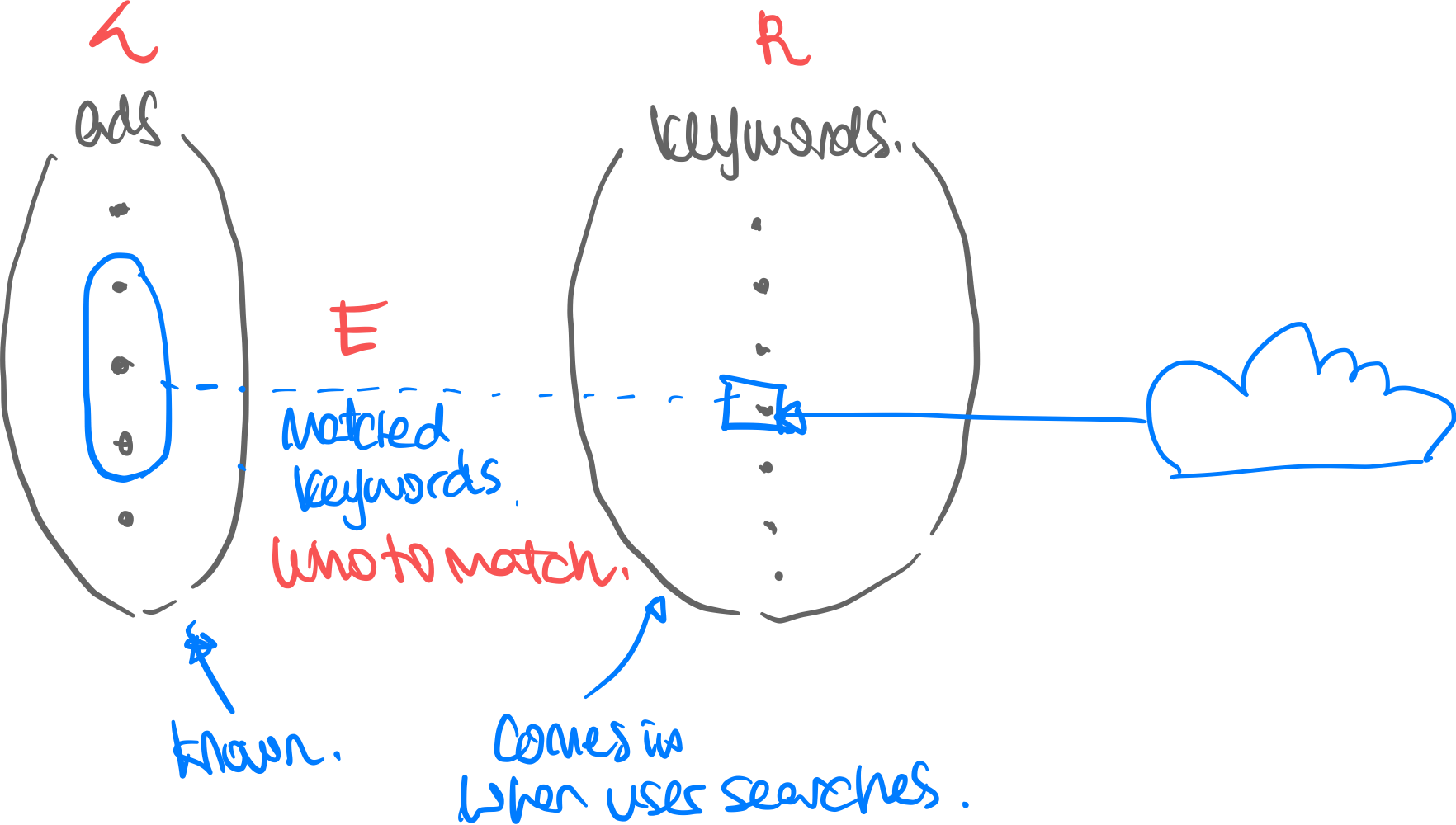
def. Optimal Online Matching Algorithm. The optimal algorithm is just one that knows in advance what all users will search, and thus simply finds a maximum partition matching.

Whole Online Matching §

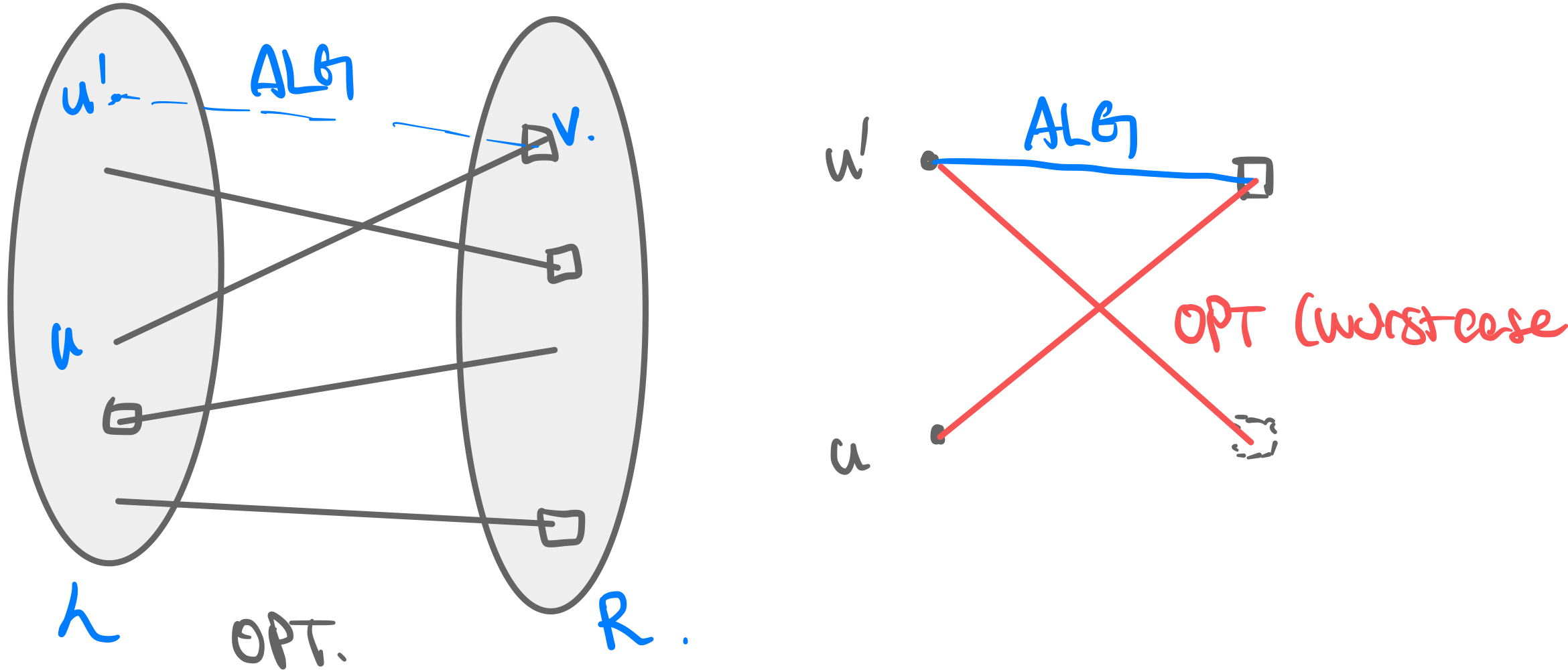
def. Greedy Online Matching algorithm. When a new user from $R$ comes in and declares its edges, it simply matches to any valid advertiser $L$.

• This simply finds the maximal (not maximum) matching.
• This is in the worst case two times worse than optimal online matching. Proof:
  1. When a new edge $v$ comes available, $\text{ALG}$ matching it to the “wrong” vertex $u^{\prime }$ will at most block two “correct matchings” (from optimal).
  2. Therefore $\frac{\text{ALG}}{\text{OPT}}\le 2$ ■

Fractional Online Matching §

We may sometimes allow for fractional matchings, i.e. consider an edge “full” at weight $1$, but the weight can be anywhere from $[0,1]$. We still benchmark fractional online matching with the original optimal whole matching algorithm.

def. Greedy Fractional Online Matching Algorithm. let $r\in R$ encountering $n_r$ edges. For every unfilled edge, equally fill $\frac{1}{n_r}$ to each. This algorithm is pretty bad. Consider the following worst case scenario:

• Each set $A,B,C,D$ have $n$ verticies
• Appears in order: $c_1,\dots ,c_n,d_1,\dots ,d_n$
• $\text{OPT}=2n$ which matches all of $A$ to $C$, and all of $B$ to $D$.
• For $\text{ALG}$:
  • consider the time when $c_i$ is matching:
    • equally gives $\frac{1}{n+1}$ to all of $b_1\dots b_n$s and $a_i$.
    • This happens for ever $c_i$, i.e. $n$ times
    • After the last vertex in $C$, total $n$ finishes matching, all of $b_1\dots b_n$ have filled $\frac{n}{n+1}$.
  • Now, each of $d_i$ only has $\frac{1}{n}$ of $b_i$ to match with.
  • Total fully matches $c_i\in C$, and $\frac{1}{n}$ of $d_i\in D$. Thus $\text{ALG}=n+\left(n\cdot \frac{1}{n}\right)=n+1$
• Thus $\frac{\text{ALG}}{\text{OPT}}=\frac{2n}{n+1}<2$. Pretty bad. def. Water-filling Algorithm. The algorithm works like this: for every $r\in R$ that appears, it outputs water at a constant rate. Fill the vertices with least water first at equal rate: 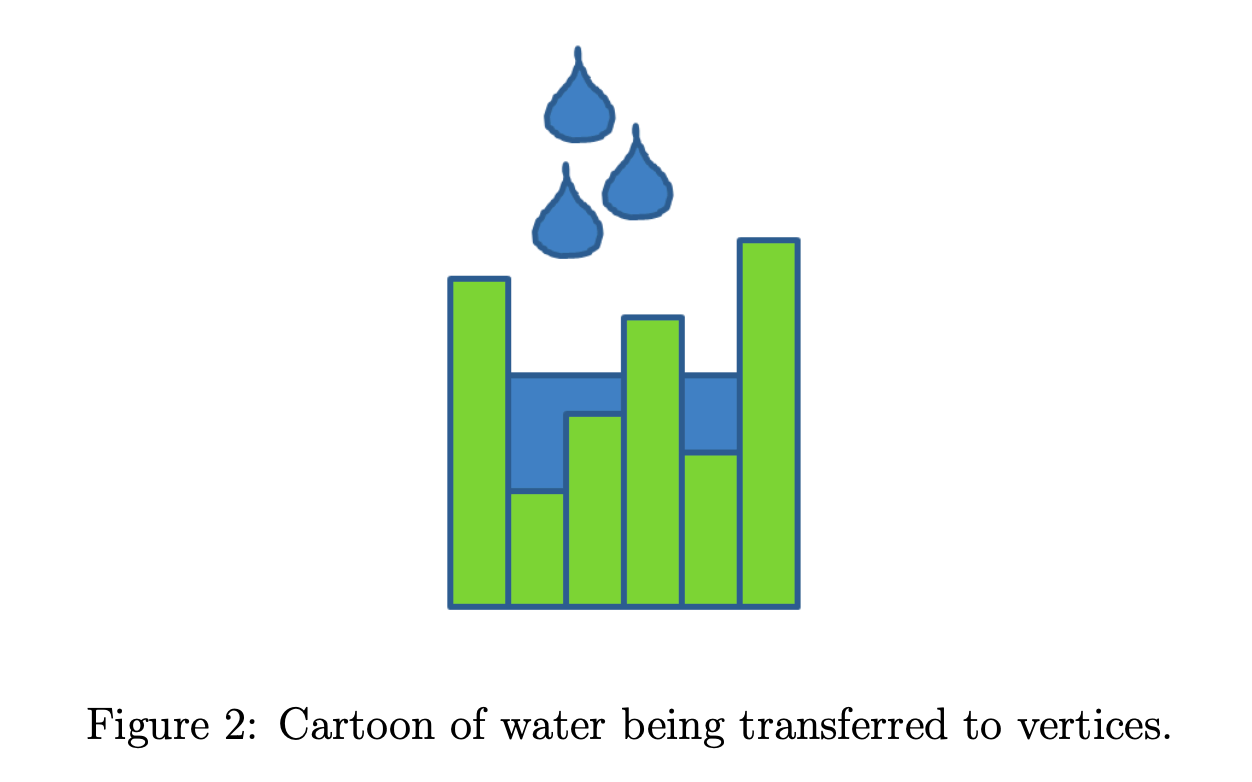In the example above of the worst-case greedy algorithm, water-filing does a better job. First consider $c_i$ filling $a_i$ and all of $b_1\dots b_n$.
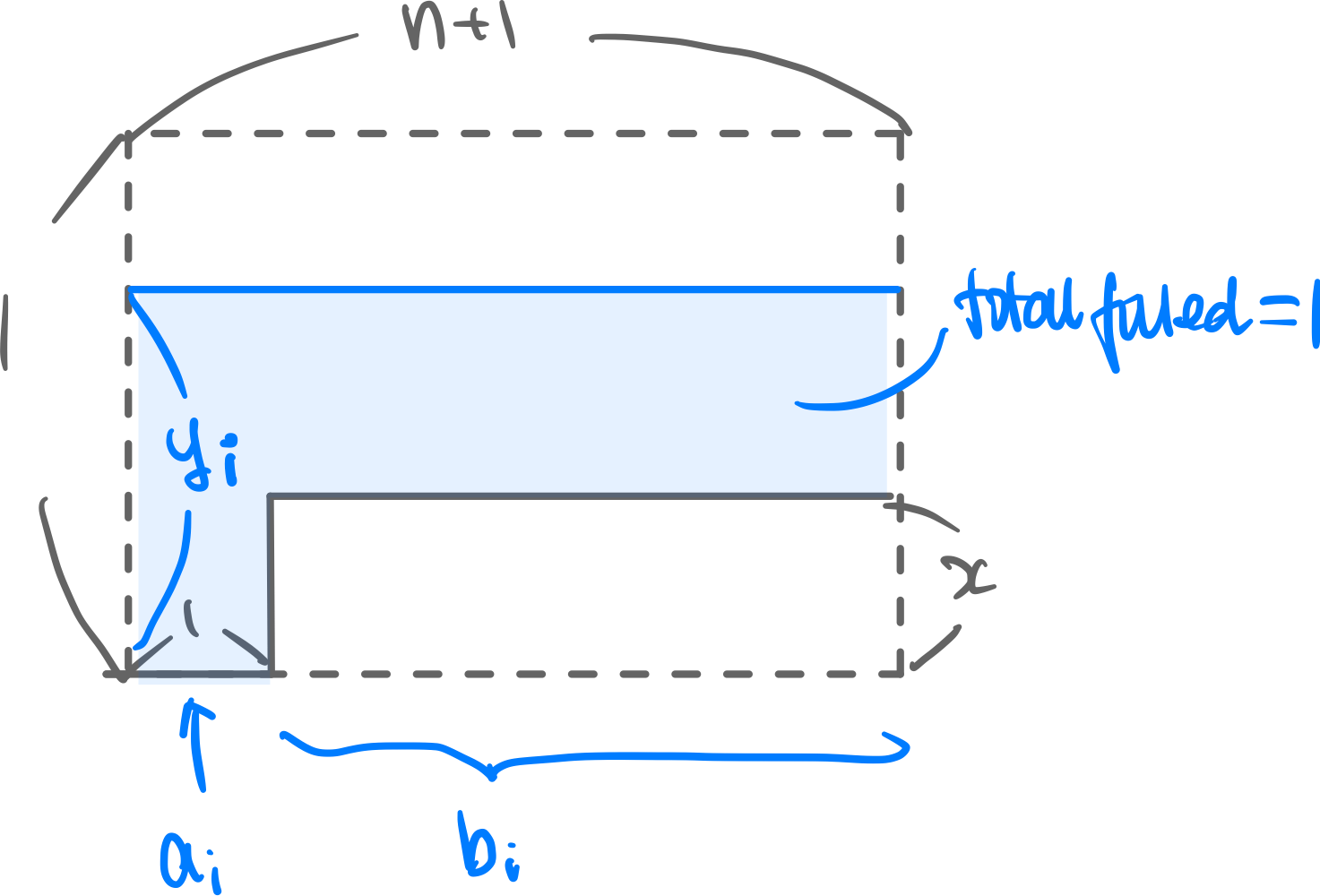
• $b_1\dots b_n$ is already filled up to level $x$ (we know they are all filled up to equal amounts, because $B$ and $C$ are fully connected.)
• $a_i$ is empty because it is only connected to $c_i$
• Total water output by $c_i$ is $1$.
• Total $n+1$ verticies.
• We know that water level will rise above $x$ for everybody (until some $y_i$) because $a_i$ can’t hold that much Then, denoting the rate of water output by $c_i$ as $\frac{dx}{dt}$:

$$\begin{array}{rl}\underset{\text{ filled by ai }}{\underbrace{x}}+\underset{\text{ filled by all vertex }}{\underbrace{\frac{dx}{dt}(n+1)}}& =\underset{\text{ total water }}{\underbrace{1}}\\ \frac{dx}{dt}& =\frac{1-x}{n+1}\end{array}$$

Then, let $y$ be the height of water on $b_1\dots b_n$ after $c_1\dots c_n$ are done filling. Summing this up for all $c_1\dots c_n$ from $x=0\dots y$ and $t=0\dots n$:

$$\begin{array}{rl}{\int }_{x=0}^y\frac{1}{1-x}dx& ={\int }_{t=0}^n\frac{1}{n+1}dx\\ [-\ln (1-x){]}_0^y& =\frac{n+1}{n+1}=1\\ \ln (1-y)& =-1\\ y& =1-\frac{1}{e}\end{array}$$

And then the remaining $\frac{1}{e}$ for each $b_i$ will be matched to $d_i$. Total matched is:

$$\begin{array}{rl}\text{ALG}& =\underset{\text{ by C }}{\underbrace{n}}+\underset{\text{ by D }}{\underbrace{n\left(\frac{1}{e}\right)}}\\ & =n\left(1+\frac{1}{e}\right)\\ & \\ \frac{\text{ALG}}{\text{OPT}}& =\frac{n\left(1+\frac{1}{e}\right)}{2n}=\frac{e+1}{2e}\end{array}$$

(Note that we still compare with whole matching optimum.)

def. Ranking Algorithm.

def. Bid Scaling Algorithm.