Traffic Routing

Similar to Maximum Flow Problem. An instance of a Potential Game.

Atomic Traffic Routing §

This time, there are $n$ cars (not infinitesimally small). If player $i$ chooses path $P_i$, then:

1. $m_e$: traffic (=# of cars) flowing thru edge $e$
2. Individual cost: $c_i(P_i,\overrightarrow{P_{-i}})={\sum }_{e\in P_i}{c}_e(m_e)$
3. Potential Function: $\varphi (\vec{P})={\sum }_{\forall e}{\sum }_{j-1}^{m_e}{c}_e(m_e)$
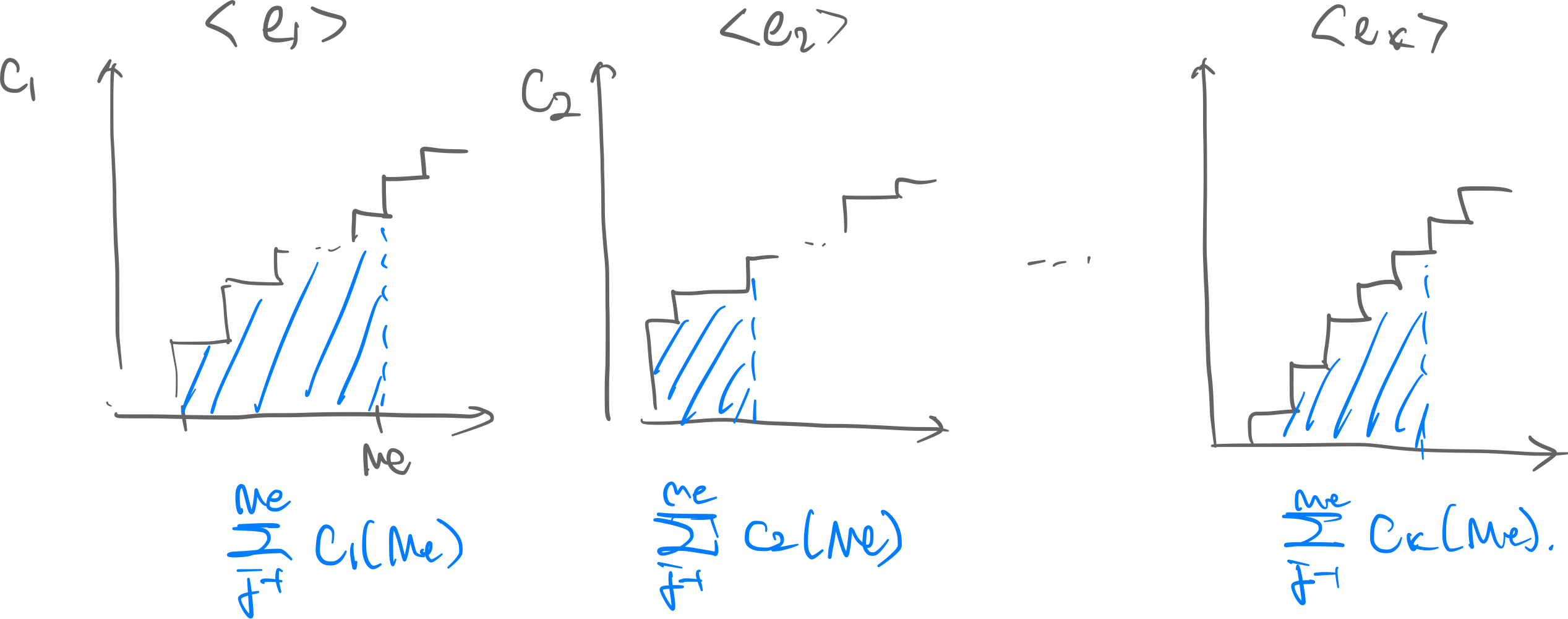
   • This is similar to the integral of costs for each edge:

thm. (Potential function minimization derives PNE) Minimizing the following potential function will give you the PNE.

$$\Phi (f)=\underset{\text{ Over every edge }}{\underbrace{\sum _{e\in E}}}\underset{\text{ Area under cost function }}{\underbrace{\sum _{i=1}^{f_e}{c}_e(i)}}$$

Proof. The inner summation above is Intuitively the area under the cost, as illustrated above. Then, consider an agent $i$ deviated from path $P_i$ to $\widehat{P_i}$, which as a whole is a change from flow $f$ to $\hat{f}$. Then the difference in potential of these two flows is:

$$\begin{array}{rl}\Phi (\hat{f})& =\Phi (f)+\underset{\text{ add deviated edges }}{\underbrace{\sum _{e\in \widehat{P_i}\setminus P_i}{c}_e(f+1)}}-\underset{\text{ remove undeviated edges }}{\underbrace{\sum _{e\in P_i\setminus \widehat{P_i}}{c}_e(f)}}\\ \Phi (\hat{f})-\Phi (f)& =\underset{\text{ i ’s cost at Pi^}}{\underbrace{\sum _{e\in \widehat{P_i}}{c}_e(\hat{f})}}-\underset{\text{ ...at Pi }}{\underbrace{\sum _{e\in P_i}{c}_e(f)}}\end{array}$$

Thus, each user’s goal is to minimize this potential function. Therefore the minimum of the potential function is the pure strategy nash eqilibirum. ■

thm. (existence of PNE). Proof outline. This potential function will have one global minimum, if the cost functions are monotonically increasing (v.v. strictly increasing) and continuous, making $\Phi$ a (v.v. strictly) convex function which has a global minimum (v.v. a single global minimum). This shows that it PNE will always exist for monotonic cost functions. ■

Nonatomic Traffic Routing §

Definitions §

• flow on edge $e$ is $x_e$
• Congestion Function $c_e(x_e)$ i.e. time taken
• Individual Delay for Path $P$: ${\sum }_{e\in P}{c}_e(x_e)$
• Total Delay for all paths: ${\sum }_{\forall \text{cars}}{\sum }_{e\in P}{x}_e\cdot c_e(x_e)$

Pigou’s Example §

• Nash Equilibrium when
  1. For all users of edge $a$, $c_a(x_a)\le c_b(x_b)$
  2. For all users of edge $b$, $c_b(x_b)\le c_a(x_a)$
  • Total delay $=(0\cdot 1)+(1\cdot 1)=1$
• Global Optimum when:

$$\begin{array}{rl}\text{Total Delay}& =(x_a\cdot 1)+(x_b\cdot x_b)\\ & =1-x_b+x_b^2\end{array}$$

⇒ Total delay minimized when half goes thru $a$, other half goes thru $b$

Braess’s Paradox §

i.e. adding a new road may worsen outcome for Nash Equilibrium (but not in global minimum)

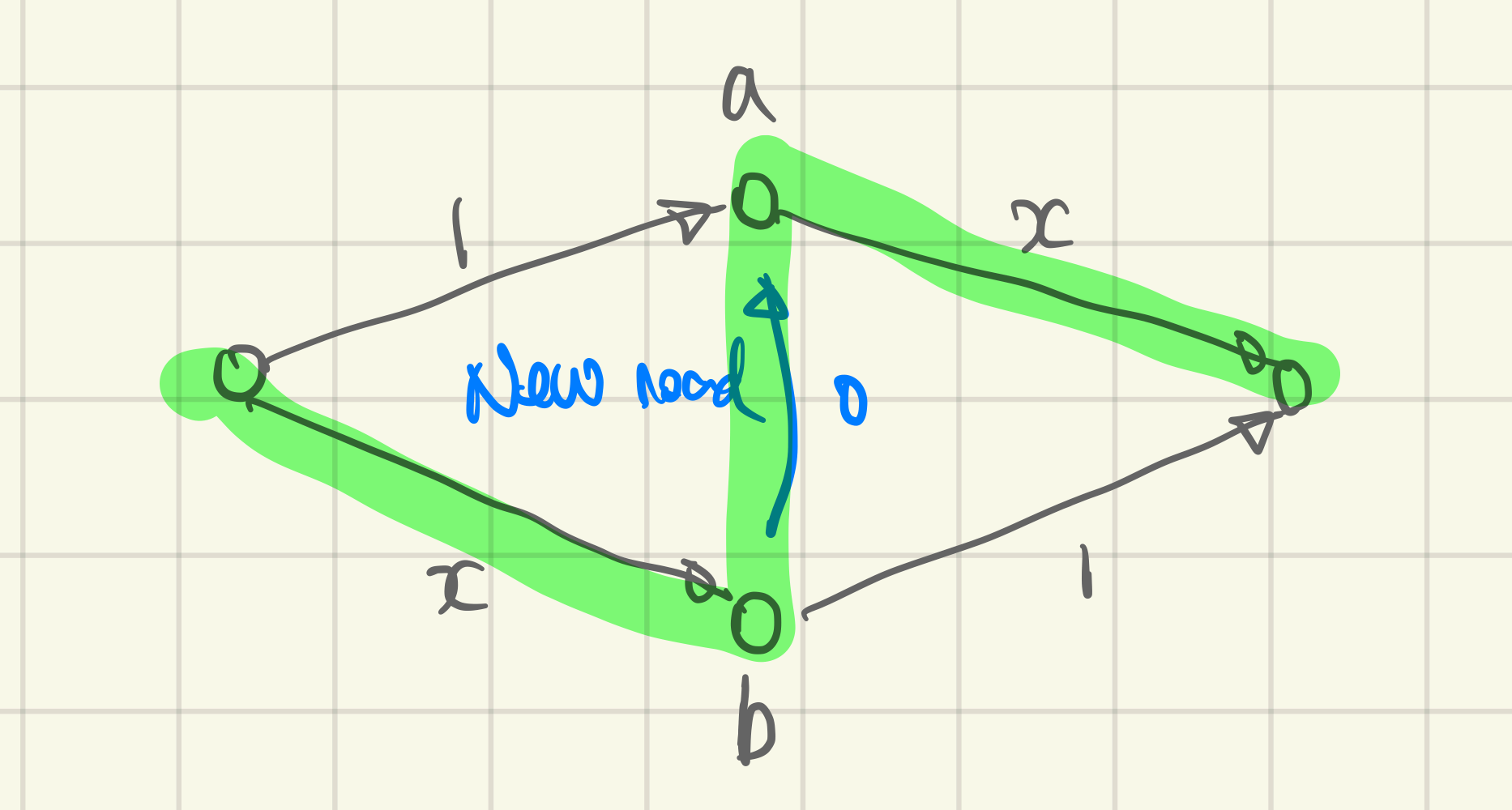
• Consider before and after adding edge from $b\to a$, a superhighway with zero delay cost.
• NE before adding blue edge:
  • $0.5$ on top ($s\to a\to t$)
  • $0.5$ on bottom ($s\to b\to t$)
  • $\text{Total Delay}=\frac{3}{2}$
• NE after adding blue edge (superhighway):
  • all passes thru green path ($s\to b\to a\to t$)
  • $\text{Total Delay}=2$ (worse!)

For Social Planner… §

Observe that congestion network is a convex optimization problem:

• Total Delay function is a convex function
• Constraints (=conversation of flow) are linear:
  1. $\forall v$ inflow = outflow
  2. $\sum$ flow at source/target is $1$
  3. $f_e\ge 0$

For Obtaining Nash Equilibirum… §

thm. Routing NE Uniqueness. For every routing problem there is only one NE.

thm. Obtaining NE of Congestion Network. Minimizing the following function $\varphi$ will yield the unique NE of any congestion network:

$$\begin{array}{r}\varphi (\vec{f})=\sum _{e\in E}\frac{a_e{f}_e^2}{2}+b_e{f}_e\end{array}$$

Proof Sketch. The following definition of $\varphi$ will satisfy the definition of a potential function

$$\begin{array}{rl}\varphi (\vec{f})& :=\sum _{e\in E}{\int }_0^{f_e}{c}_e(x)dx\\ & =\sum _{e\in E}{\left[\frac{a}{2}{x}^2+bx\right]}_0^{f_e}\\ & =\sum _{e\in E}\frac{a_e{f}_e^2}{2}+b_{e}f{}_e\end{array}$$

■