Covariance

Motivation. Let us imagine a tuple of data generated by two independent RVs: $(x_1,y_1),\dots ,(x_4,y_4)$, as graphed below.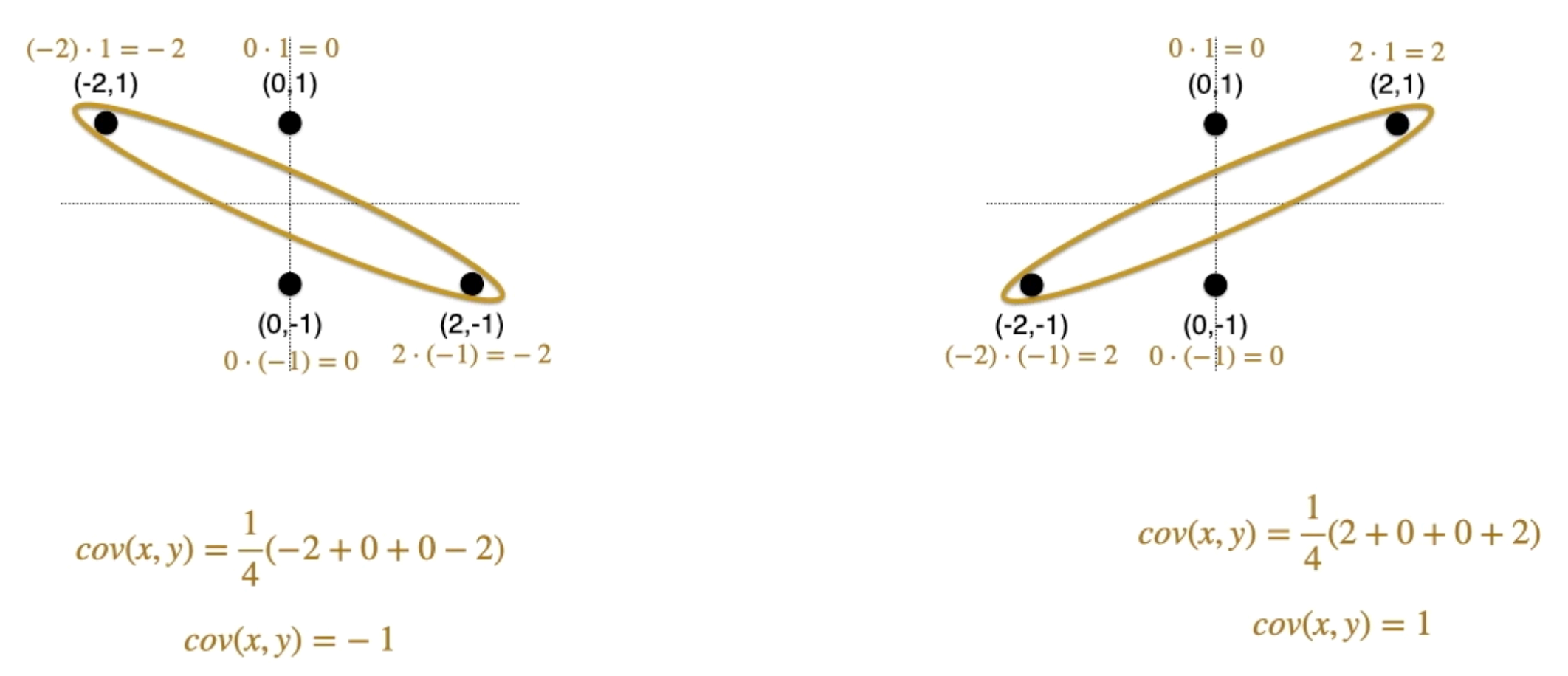

1. $\text{Var}(X)=2$ for both
2. $\text{Var}(Y)=1$ for both
3. …but the ‘spread’ of these two are clearly different! There, we observe that what matters is the ‘quadrant’ or ‘direction’ of the spread that matters, and that is captured by multiplication of the two coordinates. Thus: Intuition. Covariance is the “average quadrant” of the direction of spread. The covariance matrix from 5:06

def. Covariance. Covariance measures the joint variability of two R.V.s; let $X,Y$.

• When $X,Y$ show similar behavior, $\text{Cov}(X,Y)>0$
• When $X,Y$ show opposite behavior, $\text{Cov}(X,Y)<0$

$$\begin{array}{rl}\text{Cov}(X,Y):& =\mathbb{E}((X-{\mu }_X)(Y-{\mu }_Y))\\ & =\mathbb{E}(X\cdot Y)-\mathbb{E}(X)\cdot \mathbb{E}(Y)\end{array}$$

• When $X\perp Y$, then $\text{Cov}(X,Y)=0$; but $\text{Cov}(X,Y)$ does not imply $X\perp Y$
• Covariance is a generalization of Variance: $\text{Var}(X)=\mathbb{E}((X-{\mu }_X{)}^2)=\text{Cov}(X,X)$

thm. Relationship between Covariance and Variance. let $X,Y$. then:

$$\begin{array}{rl}\text{Var}(X+Y)& =\text{Var}(X)+\text{Var}(Y)-2\cdot \mathbb{E}((X-{\mu }_X)(Y-{\mu }_Y))\\ & =Var(X)+Var(Y)-2Cov(X,Y)\end{array}$$

• When $X\perp Y$ then $\text{Var}(X,Y)=\text{Var}(X)+\text{Var}(Y)$

thm. Bilinearity of Covariance.

• $\text{Cov}(aX,aY)=ab\cdot \text{Cov}(X,Y)$
• $\text{Cov}(X,Y+Z)=\text{Cov}(X,Y)+\text{Cov}(X,Z)$

thm. Summed Variance. let $X_1,\dots ,X_n$. Then

$$\text{Var}(\sum _i{X}_i)=\sum _i\text{Var}(X_i)+2\sum _{\forall j,k\text{ s.t.}j<k}\text{Cov}(X_j,X_k)$$

E.G. second summation has $\left(\genfrac{}{}{0ex}{}{3}{2}\right)$ terms:

$$\begin{array}{rl}\text{Var}(X_1+X_2+X_3)& =\text{Var}(X_1)+\text{Var}(X_2)+\text{Var}(X_3)\\ & +2\cdot \text{Cov}(X_1,X_2)\\ & +2\cdot \text{Cov}(X_2,X_3)\\ & +2\cdot \text{Cov}(X_1,X_3)\end{array}$$

Covariance Matrix §

def. Covariance Matrix is a collection of covariances for $X_1,\dots ,X_n$ RVs:

$$\Sigma =\left[\begin{array}{cccc}{\sigma }_{1,1}& {\sigma }_{1,2}& \cdots & {\sigma }_{1,n}\\ {\sigma }_{2,1}& {\sigma }_{2,2}& \cdots & {\sigma }_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{n,1}& {\sigma }_{n,2}& \cdots & {\sigma }_{n,n}\end{array}\right]$$

where ${\sigma }_{i,j}$ is the covariance $\text{Cov}(X_i,X_j)$

• Always symmetric
• Determinant gives