Scheduling Problem

Scheduling problem solution formulations

1. Sort by some quantity
2. Schedule accordingly
3. Prove correctness by these strategies

Event Scheduling §

Q. Interval Scheduling (Greedy Algorithm)

• Dynamic Programming idea works
  • dp[i] = max(dp[]+1
  • $O(n^3)$ time
• Greedy Algorithm is even better
  • Idea: sort by

alg. Interval Scheduling with $n$ rooms

Q. Multiple Room Interval Scheduling

Q. Interval Coloring

Q. Interval Cover Problem

Job Scheduling §

Q. Minimize Makespan (=maximum time on any machine) of $n$ machines

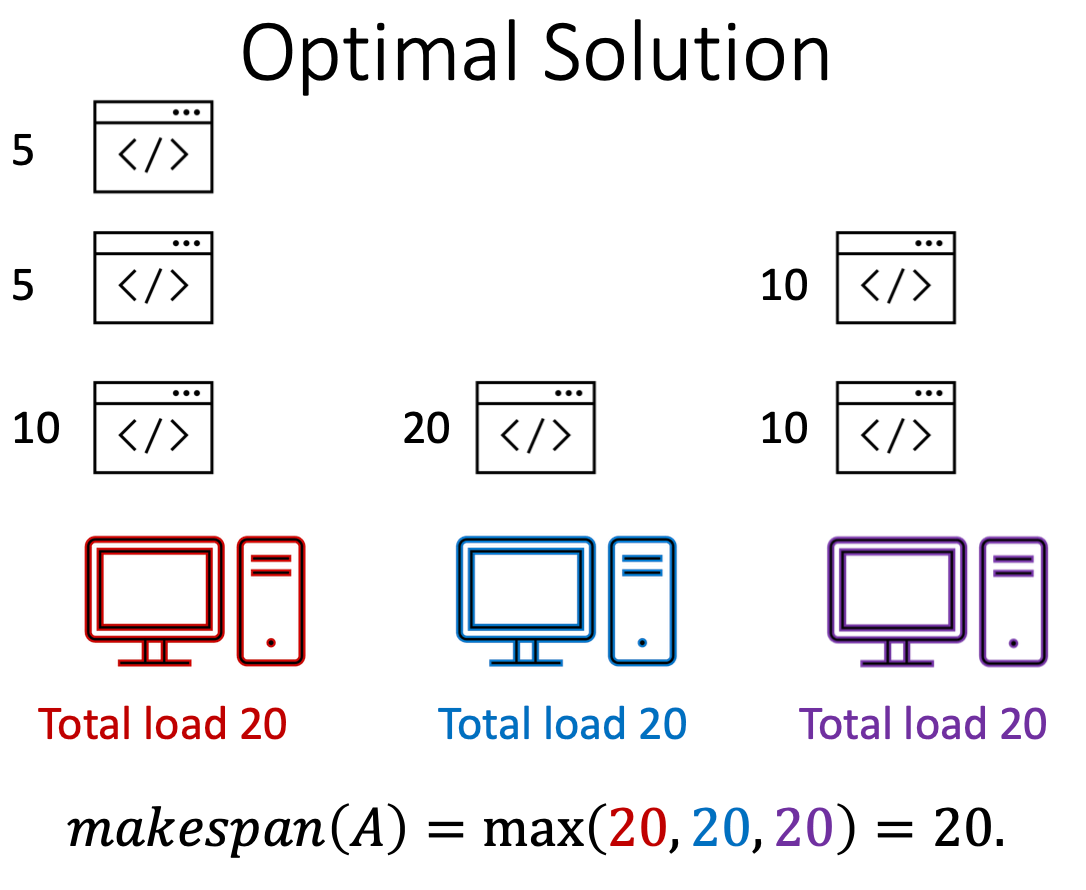
• NP-Hard problem (reduce from $\frac{1}{2}$-Subset Sum)

alg. Approximate Greedy Makespan: Always choose the least loaded machine

• Is a 2-level approximation 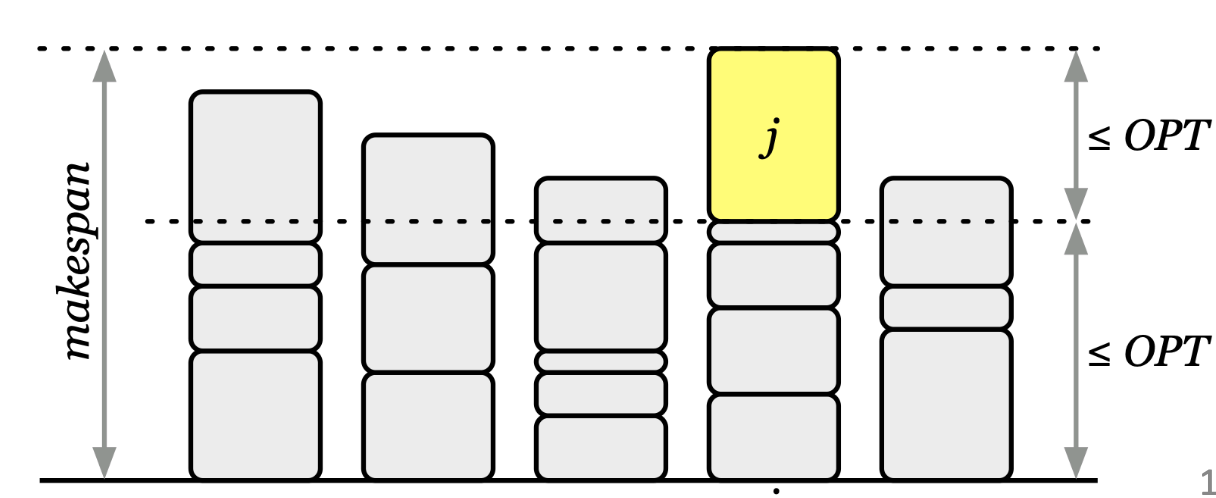alg. Better Approximate Greedy Makespan: Assign from longest to shortest job, to least loaded machine every time.

---

alg. Minimize lateness of jobs

• Interval Scheduling

  • schedule $n$ jobs
    • no dependencies
  • => how many jobs can you complete? (total time doesn’t matter!)
  • conflict when:
    • Start[i] <
  • Dynamic Programming solution is easy
    1. OPT = max(1+OPT(jobs that don’t conflict with job 1) vs OPT(2..n))
  • => but $O(n^3)$ or even with improvement $O(n^2)$!

• Greedy solution:

  • job that finishes first = job that leaves the most amount of remaining time
  • implementation
    1. Sort by finish time
    2. choose earlyest finish time
    3. choose next earliest finish time that doesn’t conflict with most recently finished job
    4. Done!
  • => $O(n\log n)$ time (because sorting)!
  • Proof by induction: Exchange Argument
    • base: $Y\ast$ optimal solution has $y_{1}in{Y}^{\ast }$
      • if you have $x_1$ that finish time earlier than $y_1$…
      • removing $y_1$ and adding $x_1$ is also optimal solution

• Try: dp solution

• variation: make span algorithm (greedy is close to optimal, but not optimal)

• interval scheduling, but with $n$ meeting rooms

  • greedy still words!

• minimum total completion time.

• minimize lateness

  • sort by ascending lateness<<