Linear Discriminant Model

Motivation. In the input space, draw a line to classify into two categories. This is achievable using linear regression

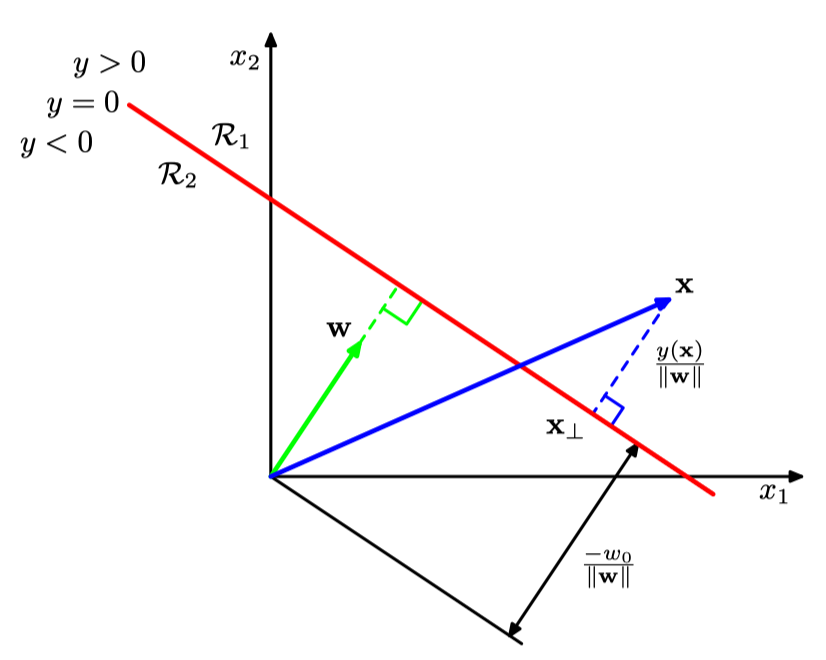
Discriminant Function §

def. Discriminant Function takes an input vector $\mathbf{x}$ and assigns into one of $K$ classes, ${\mathcal{C}}_k$.

• def. Decision Surface is the boundary that splits the classes in input space.
• def. Decision Region is the regions generated by the decision surfaces that correspond to a single class. When there is two classes, ${\mathcal{C}}_1,{\mathcal{C}}_2$ then:

$$y(\mathbf{x})=\underset{\text{ weight=params}}{\underbrace{{\mathbf{w}}^{\top }}}\mathbf{x}+\underset{\text{ bias }}{\underbrace{w_0}}$$

And assign:

$$\mathbf{x}\in \{\begin{array}{ll}{\mathcal{C}}_1& \text{if }y(\mathbf{x})\ge 0\\ {\mathcal{C}}_2& \text{if }y(\mathbf{x})<0\end{array}$$

• $\mathbf{w}$ is orthogonal to the decision surface hyperplane (via linalg; green in image)
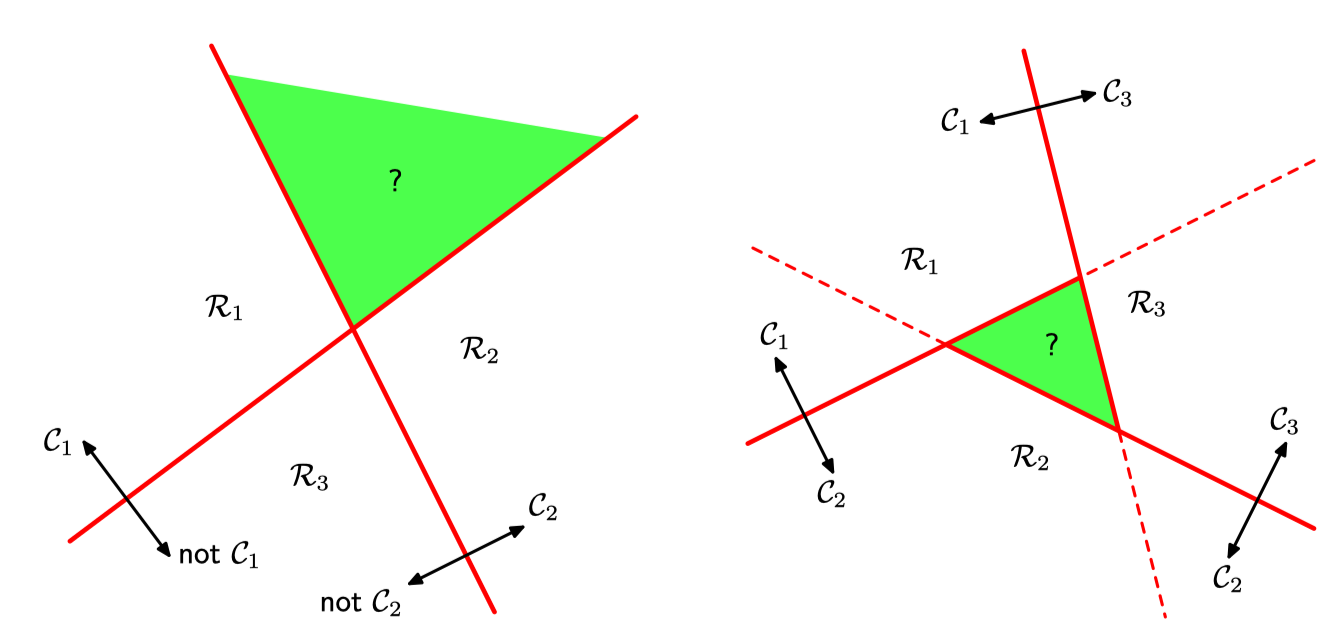• $w_0$ determines the distace from the origin of the decision surface When there are $K>2$ classes then we cant just split into $K$ regions naively because: Therefore we instead introduce a discriminant function for every pair of classes, in total $\frac{K(K-1)}{2}$ DFs for each $k\in \{0\dots K\}$:

$$y_k(\mathbf{x})={\mathbf{w}}_k^{\top }\mathbf{x}+w_{k,0}$$

and then assign to: ${\mathcal{C}}_{arg{\max }_k\{y_k(\mathbf{x})\}}$ i.e. the maximum of all discriminant functions. The pairwise decision surface for pair $j,k$ is:

$$\underset{\top }{\underbrace{({\mathbf{w}}_k-{\mathbf{w}}_j)}}\mathbf{x}+\underset{\text{ distance from origin }}{\underbrace{(w_{k,0}-w_{j,0})}}=0$$

thm. Such decision regions are singly connected and convex.¹

Linear Discriminnant Models §

def. Perceptron Algorithm. (only works for $K=2$, but is illustrative.)

$$y(\mathbf{x})=f({\mathbf{w}}^{\top }\varphi (\mathbf{x}))$$

where:

• a fixed (=non-trained) function $\varphi (\mathbf{x})$. Includes bias component.
• an activation function $f(x)$ where:

$$f(x)=\{\begin{array}{ll}1& \text{if }x\ge 0\\ 0& \text{if }x<0\end{array}$$

Optimizing the Perceptron Algorithm §

def. Perceptron Error Function.

$$E_P(\mathbf{w})=-\sum _{n\in \mathcal{M}}\underset{\text{ always >0 }}{\underbrace{{\mathbf{w}}^{\top }\cdot {\varphi }_n(\mathbf{x})\cdot t_n}}$$

where

• Sums over $\mathcal{M}$, all the misclassified $\mathbf{x}$’s
• $t_n\in \{-1,+1\}$ indicates which class it is in, ${\mathcal{C}}_1,{\mathcal{C}}_2$. Intuition. In this error function:

1. Correct classification has error $0$
2. Incorrect classification has error ${\mathbf{w}}^{\top }\cdot {\varphi }_n(\mathbf{x})\cdot t_n$ Optimizing this globally using $\nabla E_P=0$ is too computationally intensive. We instead use:

$$\begin{array}{rl}{\mathbf{w}}^{(\tau +1)}& ={\mathbf{w}}^{(\tau )}-\eta \nabla E_P(\mathbf{w})\\ & ={\mathbf{w}}^{(\tau )}+\eta \cdot {\varphi }_n{t}_n\end{array}$$

• $\tau$ is simply the learning step index
• $\eta$ is the learning rate. Adjustable Visualization. Following are two steps of a perceptron optimization.

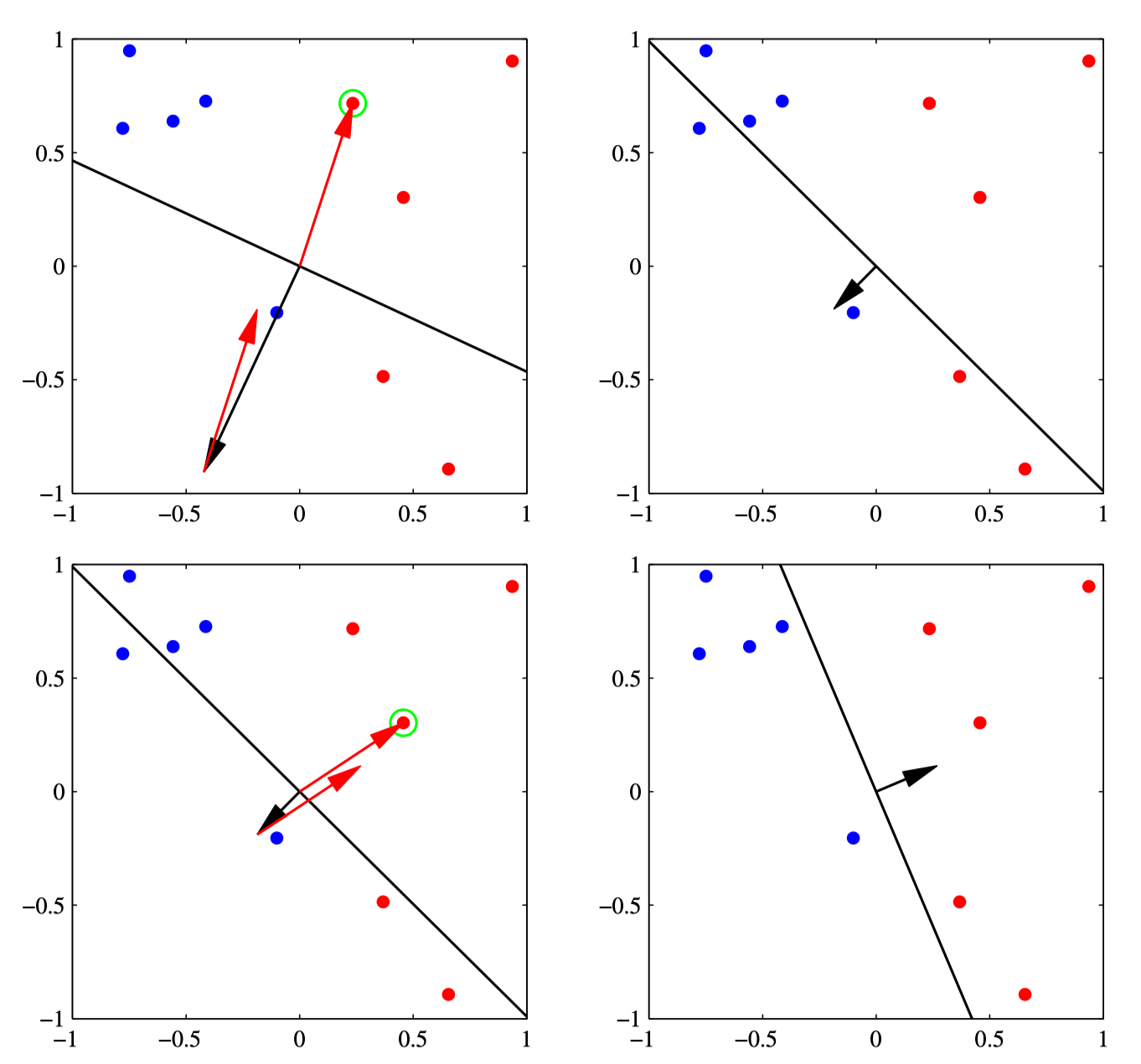
1. Top Left: decision boundary (=black line) is initialized, defined by the orthogonal vector (=black arrow). Green point is misclassified with error ${\mathbf{w}}^{\top }\cdot {\varphi }_n(\mathbf{x})\cdot t_n$ (=red arrow).
2. Top Right: error is added to the parameters to obtain a new decision boundary and new orthogonal vector.
3. Bottom Left: Green point is misclassified with error (=red arrow).
4. Bottom Right: error is added to the parameters to obtain a new decision boundary and new orthogonal vector. Motivation. We are updating for every single new data $\mathbf{x}$ that comes in. Doesn’t this mean that the error for other data may go up? No; the math says otherwise: thm. Perceptron Convergence Theorem. If the training data is linearly separable, the perceptron learning algorithm is guaranteeed to find a “exact solution” in finite steps.²

Footnotes §

1. proof ↩

2. proof ↩