Utility Function

for mapping $(p_1,p_2,I)\mapsto u$, see the Indirect Utility Function

def. Utility Function. a utility function maps $n$ goods to utility (happiness) that satisfies the assumption of Rational Taste including convexity.

$$U(\vec{x}):{\mathbb{R}}^2\mapsto \mathbb{R}$$

⇒ such that if $\overrightarrow{x_1}\succ \overrightarrow{x_2}$ then $u(\overrightarrow{x_1})>u(\overrightarrow{x_2})$

Types of Utility Functions §

Let $S_i$ be the allocation bundle to agent $i$. $S_i$ contains items (”$j$”) where $x_{ij}$ defines what percentage of that item is allocated to $j$. Then $i$’s utility ${\mu }_i$ can take various forms.

• def. Additive Utility. ${\mu }_i={\sum }_j{\mu }_{ij}{x}_j$
• def. Cobb-Douglas Utility. ${\mu }_i:={\prod }_j{\mu }_{ij}{x}_j^{{\alpha }_{ij}}$ where $\sum {\alpha }_{ij}=1$ (See the case for two goods)
• def. Leontief Utility. ${\mu }_i:={\text{min}}_j\{{\mu }_{ij}{x}_j\}$

Homothetic, Quasilinear, Perfect Substitutes §

In addition to the constrains of Rational Taste we can also have these particular tastes that characterize a utility function.

def. Quasilinear Tastes. If a utility function has quasilinear tastes against good $x_1$, then the function (or a Monotonic Transformation of the function) is linear against $x_1$, e.g.:

$$u(x_1,x_2)=x_1+f(x_2)$$

Substitutability §

def. Perfect Substitutes. If a utility function means goods $x_1$ and $x_2$ are perfect substitutes, then every indifference curve of the utility function is a linear function, e.g.

$$\begin{gathered} \text{displaylines}u(x_1,x_2)=x_1+x_2 \\ ⟹\text{setting }u=\bar{u},\bar{u}=x_1+x_2\text{is linear between}{x}_1,x_2 \end{gathered}$$

• e.g. [[Untitled 7 2.png|$5billsand$10 bills]]
• See Marginal Rate of Substitution (MRS)

Perfect Compliments.

• e.g. ![[Untitled 6 2.png|Right shoe and left shoe|380]]
• Formula looks something like: $u(x_1,x_2)=min(x_1,2x_2)$

Indifference Curves §

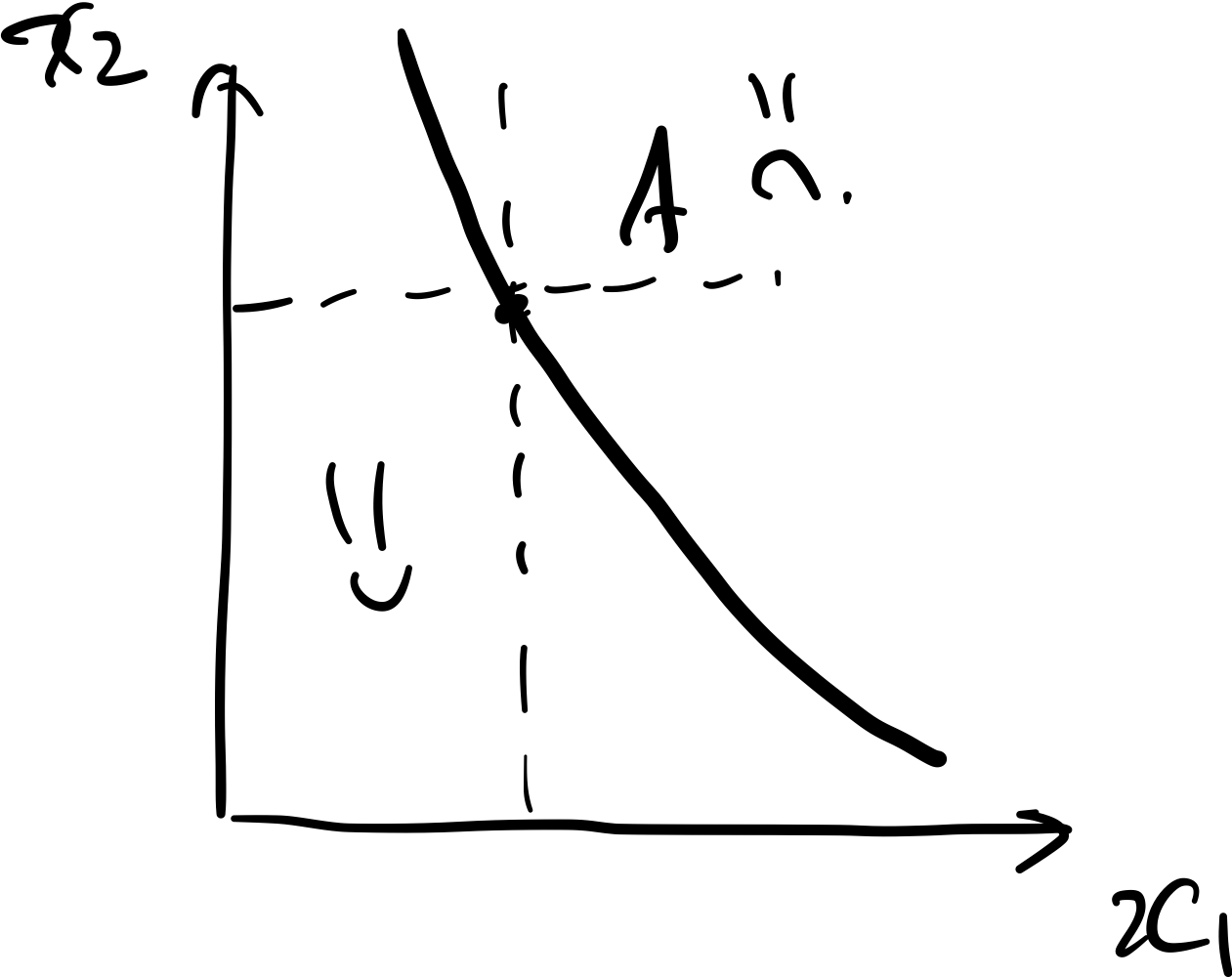
def. Indifference Curve. A set of bundles that an agent with rational taste is indifferent about

• Indifference curves are horizontal slices of a utility function.
  • i.e. a level field of a scalar field defined by the utility function of two goods—$u(x_1,x_2)$.
  • Indifference curves from the same utility function cannot cross (obviously)
• North-east side is always better.
  • ∵ monotonic taste—if this is not the case, change the direction of the curve.
• The convexity assumption causes ICs to bend to the origin
• Multiple indifference curves form one indifference map =[Utility Function]. Indifference maps are considered the same when 1. the order of the indifference curves is the same 2. MRS at every point for every curve is the same
• Budget Lines are drawn on the same graph as ICs
• When tastes are strictly convex (a taste for variety) then:
  • ⇒ $(A\succsim B)\wedge (B\succsim C)$ in the Graph

Analyzing Indifference Curve Shapes §

$$u(x_1,x_2)=x_1^{\alpha }+x_2$$