Motivation. We move on from cardinal allocations where the Utility Function is numerically defined, into a situation where there is only an ordinal ranking by the agents. This is more realistic in real life, since most people are able to identify which item they prefer even if they can’t assign it a numerical utility value. In order for any of this to be remotely fair, we need to allow probabilistic allocation. This means that the allocation solution is for each item and agent , gives a probability that the item is allocated to the agent:
For convenience, let’s also define a cumulative distribution function, for each agent.
We might visualize two different allocation for which for agent the cumulative allocation function is visualized like this:

Now we can define a few properties of baysian allocations.
def Stochastic Dominance (SD). Allocation stoastically dominates distribution for agent iff
Example. Agents want items with the preferences shown below.
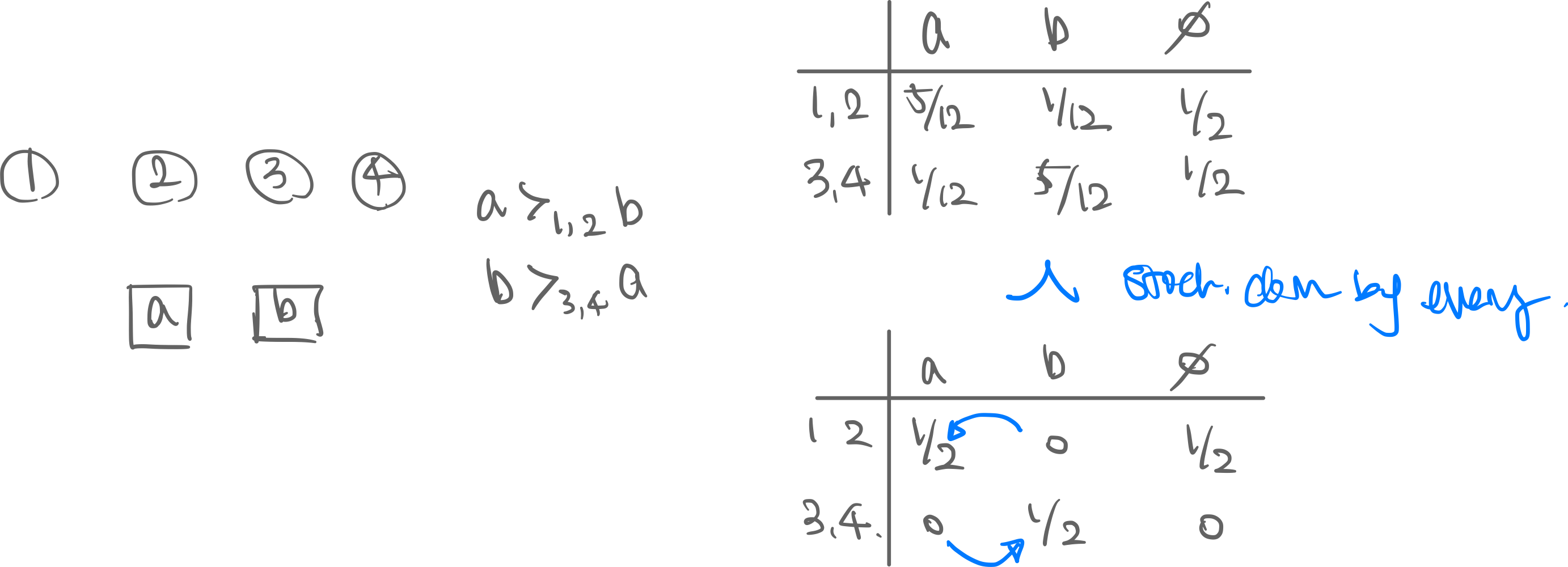
- First allocation is stochastically dominated by second allocation for agents because:
| Probability under.. | (=get sth) | ||
|---|---|---|---|
There is no item where getting gets clearly better than . Therefore stochastically dominates .
def. (Preferences in Ordinal Allocation) This is how we define preferences in ordinal situations. stochastically dominates for is equivalent to saying .
- ! But note that we cannot say anything about indifference. Stochastic dominance is defined over a partial ordering (we won’t go into more detail) which means there cannot be two different sets is indifferent about.
We define Fairness (Economics) in the following ways:
def Ordinal Efficiency (OE). Allocation is pareto-optimal when there does not exist any other allocation which is a pareto improvement than :
- Nobody are worse off:
- Some are improved:
def. Ex-Post Pareto Optimality. Allocation is Ex-post PO when every possible matching in the distribution is Ordinally Efficient.
There are two definitions of envy-freeness in probabilistic allocations:
- def. Weak Envy-Free (WEF). Allocation is WEF when there exists no that stochastically dominates for .
- def. Strong Envy-Free (SEF). Allocation is SEF when it stochastically dominates all other agent’s allocation.
Random Dictatorship
- Proofs of various ordinal allocation schemes#task
thm. RD is DSIC. Trivially. You are best off when you choose your item on the first try. Induction.
thm. RD is Ex-post PO. Trivially. If there are at least as many agents as items, then every agent picks their favorite among that’s left, and nobody can really improve by swapping. Induction.
thm. RD is WEF. (will not prove)
thm. (Not strong envy-free.) Counterexample.

- agent ’s allocation’s cumulative allocation is
- agent ’s allocation’s cumulative allocation w.r.t. ’s preferences is
thm. (RD is not ordinally efficient.) Counterexample. (Same example from above)

Proportional Eating
thm. PE is not truthful. Counterexample. 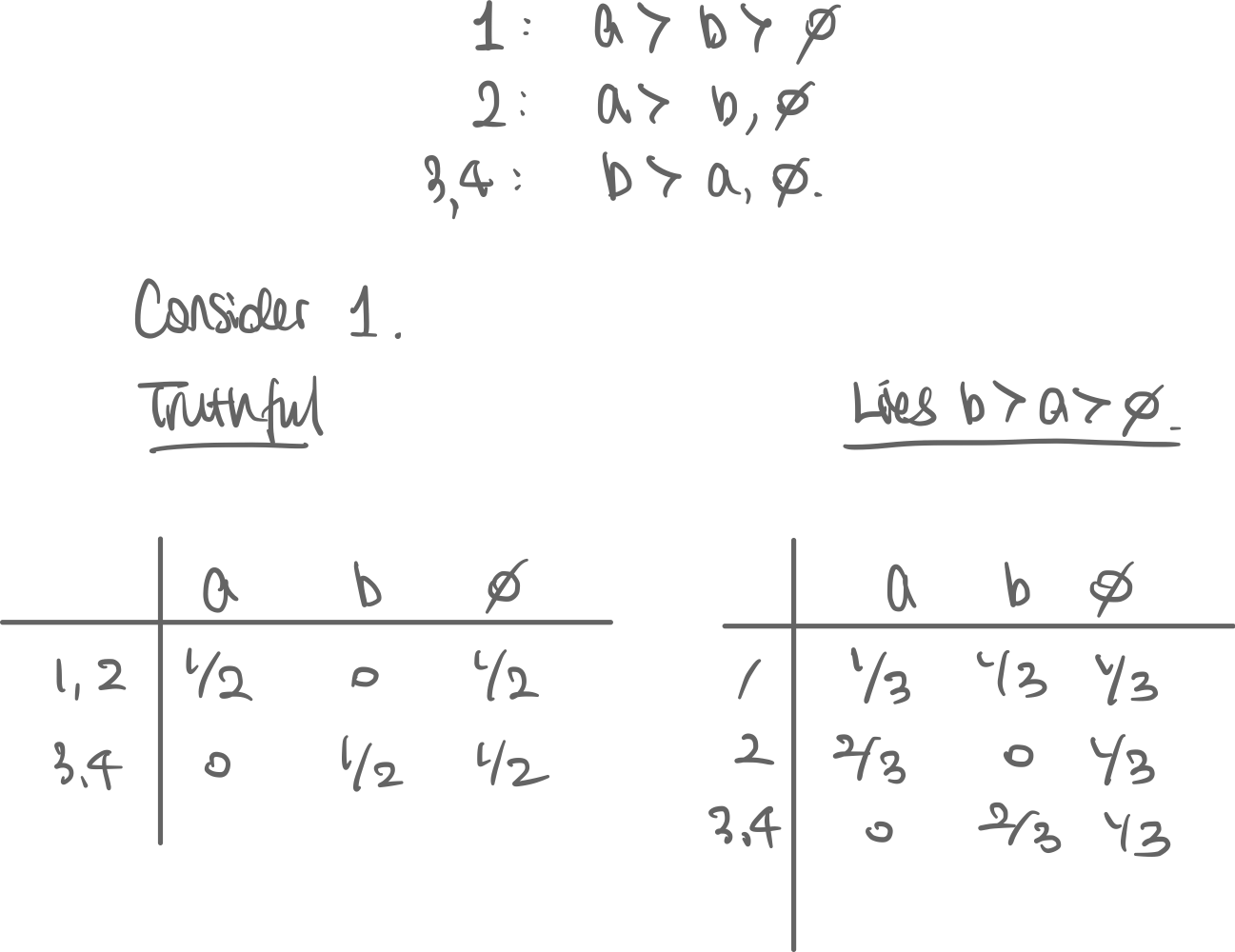
thm PE is SEF if all agents have different preference orderings (WEF if exists two agents with same ordering). Proof sketch by induction:
- Let be the timepoint is fully eaten, when is fully eaten, and so on.
- Let agent have preference of items of set . Then, agent eats first. Everybody eats at the same rate, so there is no agent who can eat even more than agent . Agent eats it from time to :
Then, moves on to eat from time to . No other agent can eat more of AND than agent (unless they both eat identically):
Induce into all items:
(equality when have identical preferences). Considering all of these cases together:
Therefore does not envy anybody else. ■
thm PE is Ex-Post PO. We will go through a lemma first. def. In allocation , call (” tau-s ”) iff there exists an agent which prefers over , but has also eaten some of (and obviously ate beforehand). Allocation-wise, and . Lemma. If an allocation is not Ex-Post PO, then there exists a cycle, i.e. Then Proof by contradiction. Assume produces and allocation that is not EX-post PO; by the lemma this allocation must have a tau-cycle: For the tau’ing in this cycle, Find the agent that tau’ed these items. Let the timepoint when starts eating be . By this time must have been fully eaten; thus . We can do this for every tau’ed agent in the cycle. But then , but by cycle . This is a contradiction. Thus allocation which is produced by PE must be Ex-Post PO. ■ Proof Sketch of Lemma. Assume allocation which is not ex-post PO, i.e. there exists another allocation where some agent is better off in , i.e. (= stochastically dominates .) Focus on this agent . Then, there must exist for this agent a pair of items (call them ) where:
- because for is better because it eats more of the better one.
- because probability for each row must both sum to .
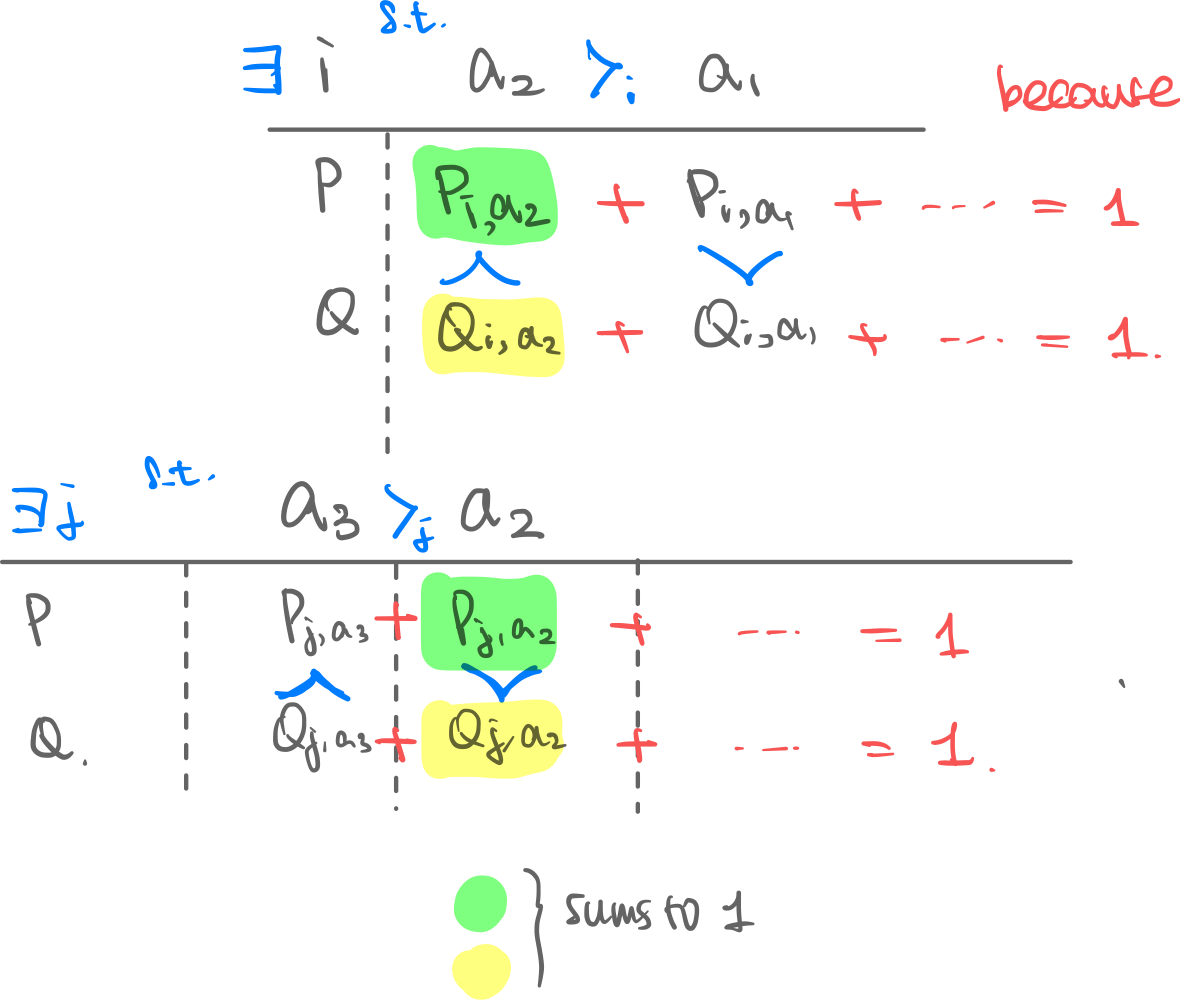 Thus and in alloc. , . Then, find another agent that . This exists because probability of each column sums to (for each allocation).
Now, for this agent , find item that satisfies:
Thus and in alloc. , . Then, find another agent that . This exists because probability of each column sums to (for each allocation).
Now, for this agent , find item that satisfies: - This item must exist because row must sum to one. Then and in alloc. We can continue on but we must form a cycle of tau-ing because there are finite number of items. ■