Shortest Path

Summary of All Shortest Path Algorithms §

Shortest Path (SP) Algorithms	BFS	A*	Dijkstra’s	Bellman Ford	Floyd Warshall
Complexity	$O(V+E)$	$O(E\log V)$	$O((V+E)\log V)$	$O(VE)$	$O(V^3)$
Recommended graph size	Large	Large	Large/Medium	Medium/Small	Small
All-Pairs	Only works on unweighted graphs	No	Ok	Bad	Yes
Can detect negative cycles?	-	-	-	✓	✓
SP on graph with unweighted edges	✓(Best)	✓	✓	✓(Bad)	✓(Bad)
SP on graph with weighted edges	Must expand graph	✓(Best)	✓	✓	✓(Bad)

Single Source Shortest Path (SSSP) §

alg. BFS Shortest Path

• Assumption: Graph doesn’t have weights
• Idea: BFS, but every time you encounter a tense edge, relax it

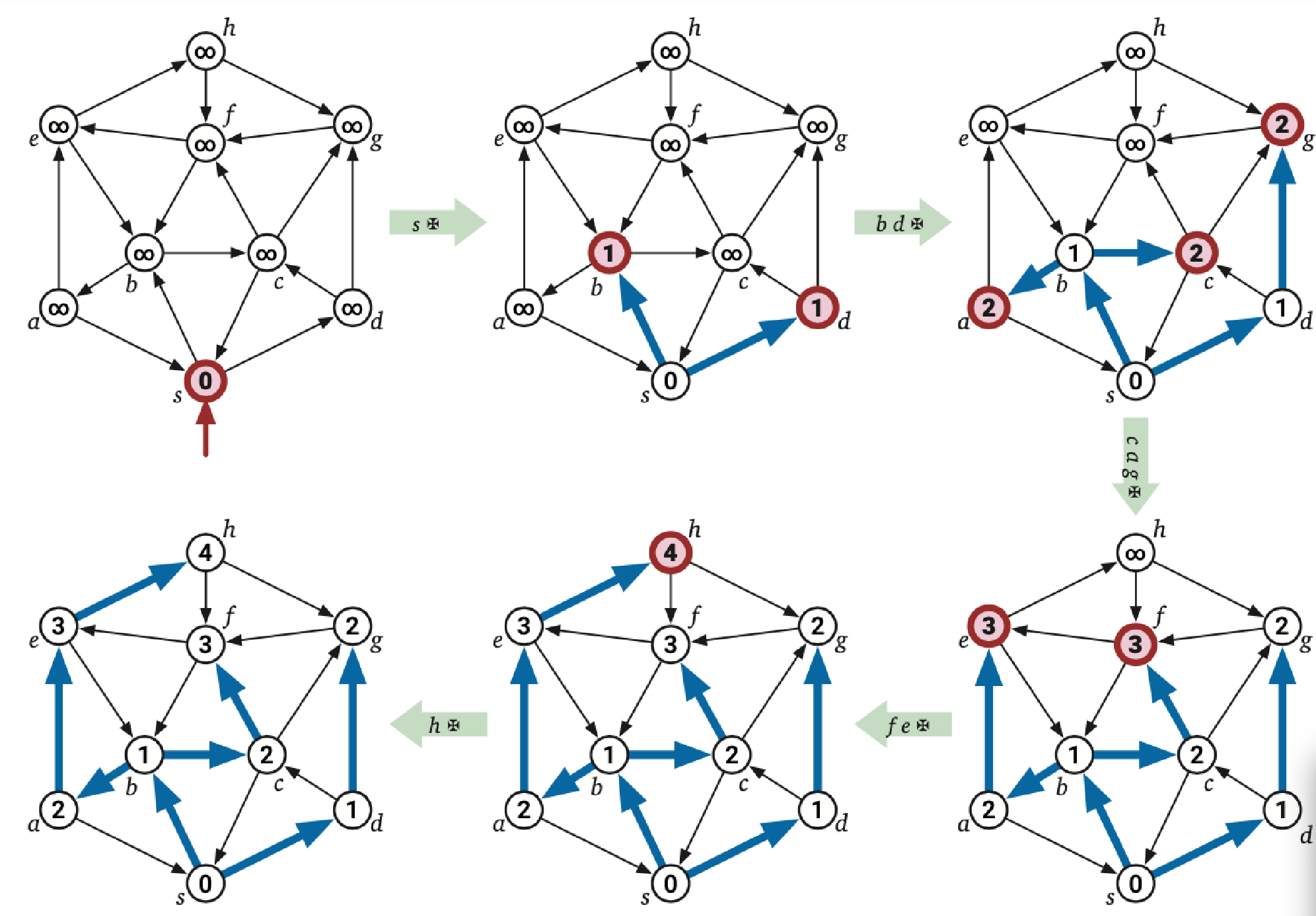
alg. Dijkstra’s Shortest Path

• Assumption. graph has non-negative edge weights
• Idea. BFS Shortest Path, but you choose the next vertex by how likely they are to be the shortest path (=maintain a Priority Queue based on path length)
  • See Dijkstra’s Algorithm - Computerphile - YouTube
• Complexity
  • Time: $O((|V|+|E|)\cdot \log |V|)$

alg. A-Star (A*) Shortest Path

• Assumption. graph has non-negative edge weights
• Idea. Dijkstra using Priority Queue, but the priority is calculated on a heuristic
  • See A* (A Star) Search Algorithm - Computerphile - YouTube
• Complexity.
  • Time: $O(|E|\log |V|)$ using binary heap

alg. Bellman–Ford Shortest Path

• Idea:
  • Repeat BFS edge relaxation for $|V|-1$ times. Get shortest path
  • Repeat BFS edge relaxation again, for $|V|-1$ times. But this time, if any cost values are updated, the node is part of a negative cycle. Mark cost to that node as $\infty$.
  • See Bellman Ford Algorithm | Graph Theory - YouTube
  • Able to deal with negative edges/negative cycles
  • Often used in finance for identifying No-Arbitrage opportunities.
• Complexity. Time: $O(V\cdot E)$

All Pairs Shortest Path (APSP) §

alg. Floyd-Warshall Shortest Path

• Idea: Dynamically Programmed algorithm. from $i$ to $j$, compare the two paths:
  1. $i\to j$ using only vertices $1,\dots ,k-1$
  2. $i\to k\to j$, but only using vertices $1,\dots ,k-1$
  3. Take the smaller of the two.
  • Example:
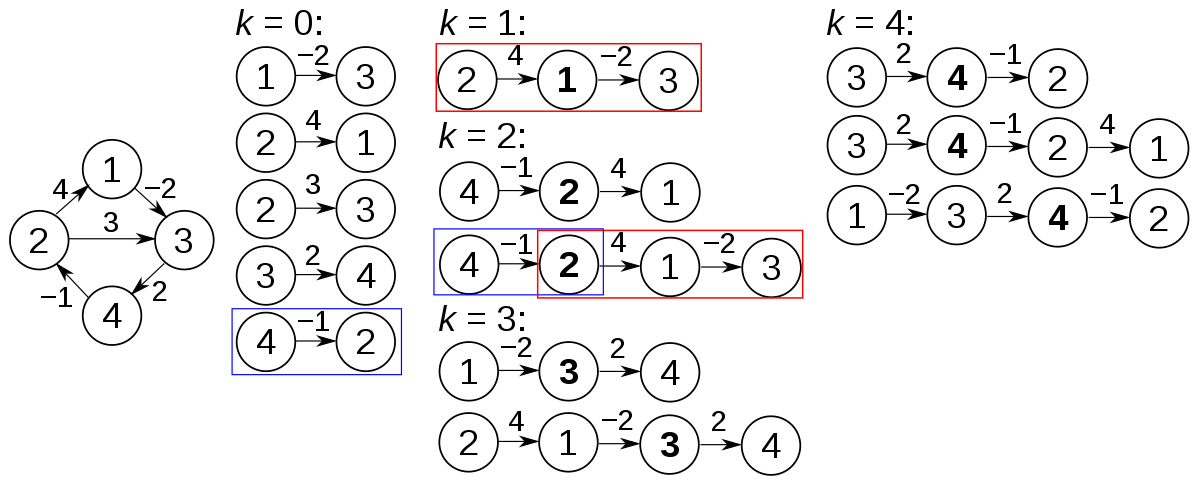
  • DP Table: $memo[k][i][j]$ is the shortest path from $i\to j$ using nodes $\mathrm{1..}k$
  • See also: Floyd–Warshall algorithm - Wikiwand
• Complexity. Time: $O(V^3)$, Space $O(V^2)$ by retaining most recent only

Tips and Tricks §

• If the problem demands you multiply edge weights instead of summing them, use $\log$ of weights instead to transform it back into a problem with summation of edge weights. (See Example)