Auction Theory

def. Sealed Bid Auction. An auction is a game where there are a certain number of buyers, buyers each have their value, $v_i$ and bid, $b_i$. The auction process takes in the bids of all buyers $\vec{b}$, and outputs the allocation $\vec{x}(\vec{b})$ and price $\vec{p}(\vec{b})$.

• $\vec{x}=⟨x_1,\dots ,x_i,\dots ,x_n⟩$ where $x_i$ is the allocation for buyer $i$
• $\vec{p}=⟨p_1,\dots ,p_i,\dots ,p_n⟩$ where $p_i$ is the price charged for buyer $i$
• e.g. if there is one item to be sold, and the i-th player gets it, then:
  • $\vec{x}=⟨0,\dots ,0,1,0,\dots ,0⟩$
  • \vec{p}= \langle 0,\dots,0,\9.37,0,\dots0 \rangle$
• Nobody except $i$ knowns their true value: $v_i$

def. Quasilinear Utility Model. Each bidder, after the auction process finishes, has utility and welfare:

$$\underset{\text{utility}}{\underbrace{{\mu }_i(\vec{b})}}=\underset{\text{welfare=value}}{\underbrace{v_i{x}_i(\vec{b})}}-p_i(\vec{b})$$

Types of Auctions §

Remark. An auction can be not DSIC and welfare-maximizing 🤯.

• Single-Item
  • Deterministic Valuations
    • Second Price (DSIC, Welfare-Max)
    • First-Price (Revenue-Max)
  • Bayesian values
    • Vickery Auction with Reserve (DSIC if regular, Revenue-max)
• Multi-Item
  • Single-item Demand, Indivisible (=sponsored search)
    • Generalized Second Price (Welfare-Max)
    • Virtual Second Price (Revenue-Max)
  • Combinatorial Demand, Indivisible
    • VCG Auction (DSIC, Welfare-Max)
    • Ascending Item Price → W.E. (Welfare-Max)
  • Combinatorial Demand, Indivisible—Price discriminatory
    • Ascending Individual Bundle Price → C.E. (Welfare-Max)
  • Combinatorial Demand, Indivisible, Bayesian
    • ? (Welfare-max)
    • ? (Revenue-max)

Properties of an Auction §

Motivation. An auction’s goal is to:

• Make sure each person tells the truth, i.e. $v_i=b_i$
• Maximize total utility, i.e. $\sum {\mu }_i$
• Sometimes, to maximize seller revenue. Therefore, we want an auction that will satisfy the following two properties.

def. Welfare Maximizing (=Socially Efficient). An auction is welfare-maximizing iff Given all bidders are truthful, then it maximizes ${\sum }_{\forall i}{v}_i{x}_i(\vec{b})$

def. Dominant Strategy Incentive Compatibility (DISC). Intuition: all bidders are incentivized to tell the truth. An auction is DISC iff:

$$\forall i,\forall b,\text{regardless of }{\vec{b}}_{-i},\underset{\text{utility for telling truth}}{\underbrace{{\mu }_i(v_i,{\vec{b}}_{-i})}}\ge \underset{\text{utility for lying}}{\underbrace{{\mu }_i(b_i,{\vec{b}}_{-i})}}$$

def. Revenue Maximizing (=Optimal). See Revenue-Maximizing Auctions.

Myerson’s Lemma (or, How to Be DSIC) §

Motivation. Instead of directly showing that an auction mechanism is DSIC, it is enough for it to satisfy the properties of the following Myerson’s lemma.

thm. Myerson’s Lemma. An auction is DSIC (=truthful) if and only if it satisfies the following to properties:

1. Given other agent’s bids ${\vec{b}}_{-i}$, the allocation function $x_i(b_i,)$ is a monotonically increasing function
   1. i.e. if $b_i^{\prime }>b_i$ then $x_i(b{’}_i,b_{-i})\ge x_i(b_i,b_{-i})$
2. Given ${\vec{b}}_{-i}$, the optimal price $p_i(b_i)=b_i{x}_i(b_i)-{\int }_0^{b_i}{x}_i(z)dz$

Proof. Property 1. Allocation is monotonic w.r.t. bid amount. (=bid more, get more) proof. By definition of DSIC, both of the following holds:

• reports $b_i$, actual value $v_i$: $v_i{x}_i(v_i)-p_i(v_i)\ge v_i{x}_i(b_i)-p_i(b_i)$ ⇒ $v_i[x_i(v_i)-x_i(b_i)]\ge p_i(v_i)-p_i(b_i)$
• reports $v_i$, actual value $b_i$: $b_i{x}_i(b_i)-p_i(b_i)\ge b_i{x}_i(v_i)-p_i(v_i)$ ⇒ $p_i(v_i)-p_i(b_i)\ge b_i[x_i(v_i)-x_i(b_i)]$
  • This is an argument from the fact that for any $\vec{b},\vec{v}$ DSIC guara ntees it’s the best possible From the two inequalities we get

$$\begin{array}{r}{v}_i[x_i(v_i)-x_i(b_i)]\ge \cdots \ge b_i[x_i(v_i)-x_i(b_i)]\end{array}$$

Thus $(v_i-b_i)[x_i(v_i)-x_i(b_i)]\ge 0$ ∎

Intuition. $v_i-b_i$ and $x_i(v_i)-x_i(b_i)$ have the same signs. Which means $x_i$ is monotonically increasing.

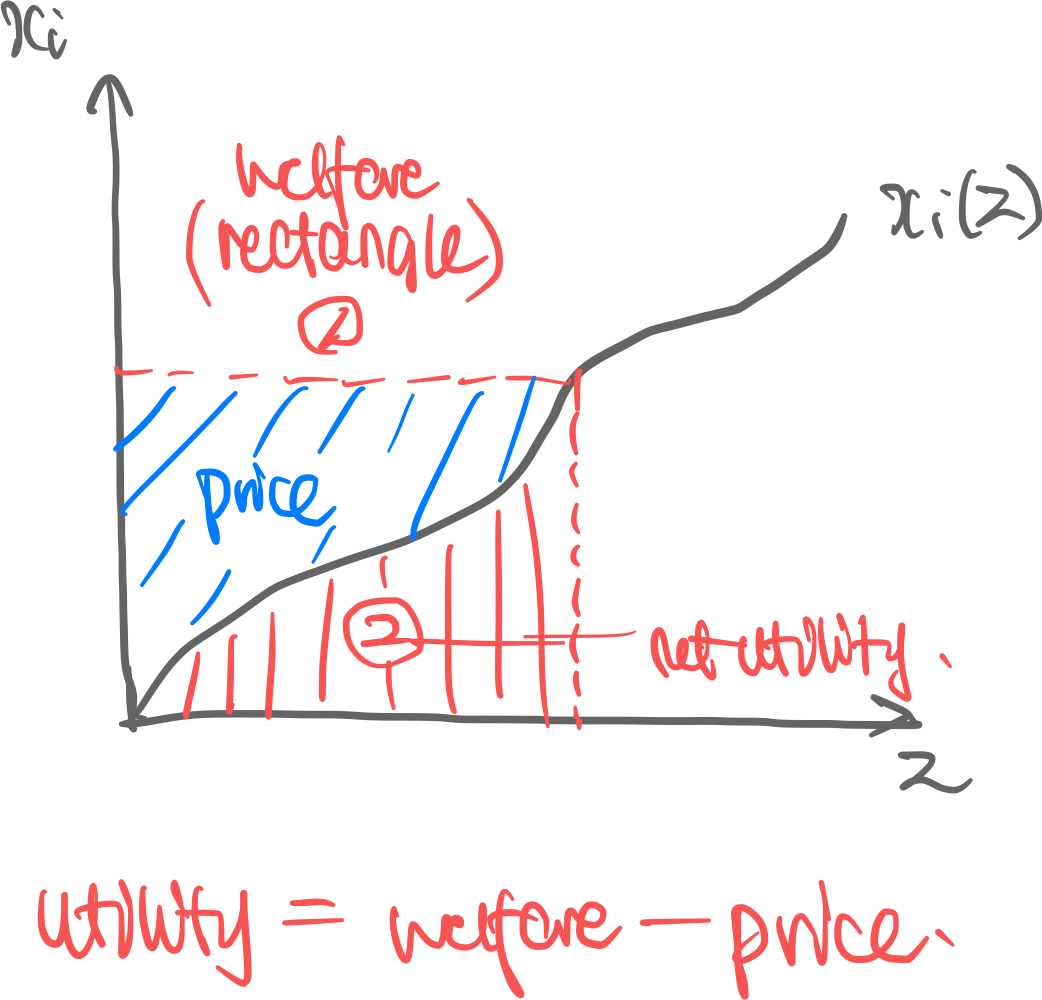
Property 2. Optimal Price. From the two inequalities in property 1 we get

$$v_i[x_i(v_i)-x_i(b_i)]\ge p_i(v_i)-p_i(b_i)\ge b_i[x_i(v_i)-x_i(b_i)]$$

We take the limit by pushing $v_i,b_i\to v$

$$v{x}_i^{\prime }(v)\ge p_i^{\prime }(v)\ge v{x}_i^{\prime }(v)$$

Thus $v{x}_i^{\prime }(v)=p_i^{\prime }(v)$. And integrating both sides

$$\begin{array}{rlr}v{x}_i^{\prime }(v)=p_i^{\prime }(v)& ⟹{\int }_0^{v}z\cdot x_i^{\prime }(z)dz={\int }_0^v{p}_i^{\prime }(z)dx& \text{substitute }z\\ & ⟹{\int }_0^{v}zd(x_i(z))=p_i(v)& \\ & ⟹p_i(v)=v{\int }_0^{v}1d(x_i(z))-{\int }_0^{v}1\cdot x_i(z)dz& \text{integration by parts}\\ & ⟹p_i(v)=v{x}_i(v)-{\int }_0^v{x}_i(z)dz& \end{array}$$

■ Intuition. The geometric intuition for this is that the price for the allocated person is the rectangle minus the area under the graph, i.e. the blue region.