Sorting Algorithms

Abstract

Best sort algorithm (merge sort) will take $O(n\log n)$ at worst.

Quick Sort §

Idea:

1. Choose pivot
2. Everything left of pivot is smaller, everything right of it is bigger ($O(n)$)
3. Call quicksort on the left side and right side

Choosing a good pivot

• Random
  • With high probability pivot within $\frac{1}{3}\sim \frac{2}{3}$
  • Likely Complexity: $T(n)\le T\left(\frac{2}{3}n\right)+cn=O(n)$
• DSelect i.e. Median of medians approach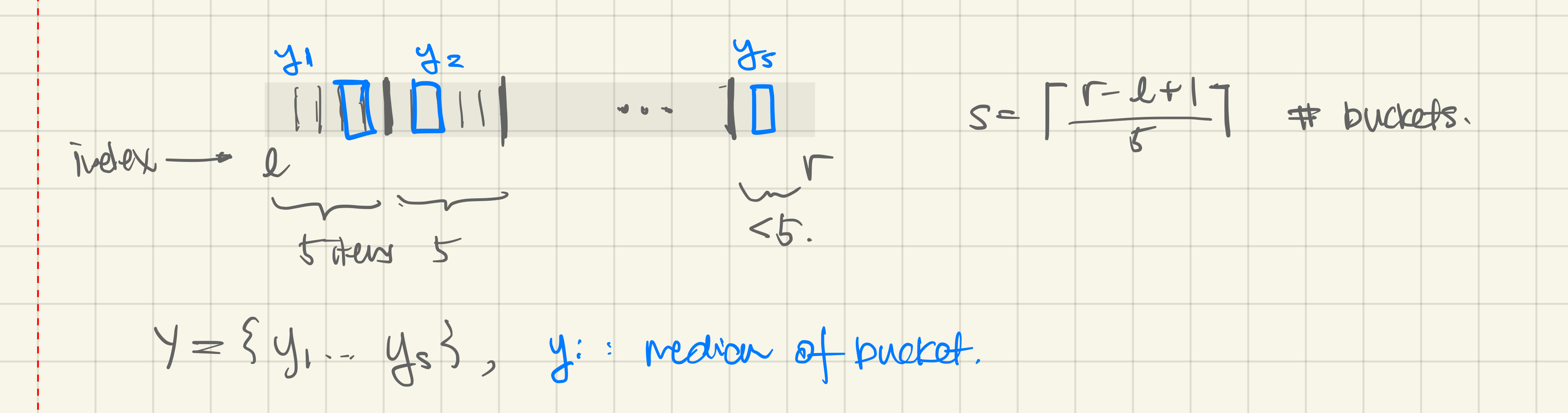
  • Rank is guaranteed to be between $\frac{1}{4}\sim \frac{3}{4}$ of the array slice
  • Complexity: $T(n)\le T(\frac{n}{5})+T\left(\frac{3}{4}n\right)+cn=O(n)$ ……first term: DSelect, second term quicksort
    • → $T(n)<A\cdot n$ for some $A\ge 20c$ (=$O(n)$)

Merge Sort §

Idea:

1. Split into two
2. Call mergesort on each left, right side
3. merge left, right side in $O(n)$ time

alg. Parallel Merge Idea: For the 8 elements shown below, can we find out how to place the element in parallel (8 simultaneous processes)? → We can!

• Left half: binary search on right half for correct place
• Right half: binary search on left half for correct place

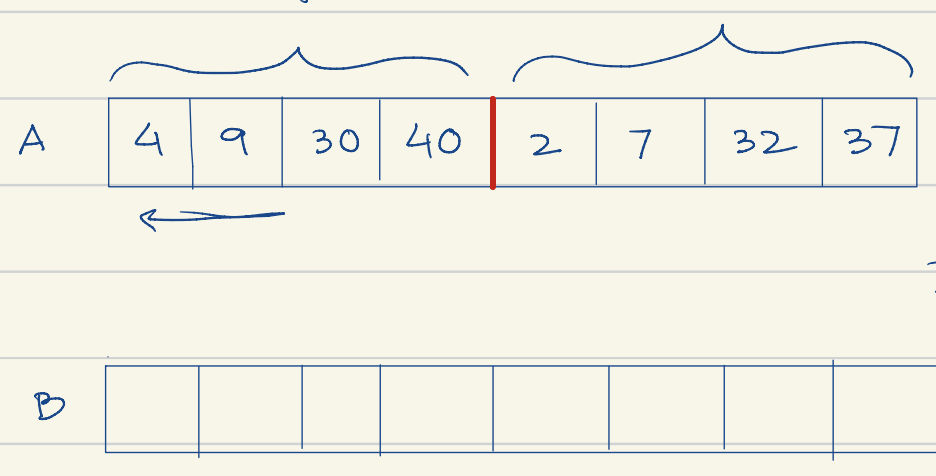
def PMerge(A[1..n], m)
	# Ind[i] stores the final index of the i-th element
	
	# left half
	parallel for i=1 to m
		# search in right half
		Ind[i] <- BinarySearch(in A[m+1..n] for A[i]) + i
	# right half
	parallel for j=m+1 to n
		# search in left half
		Ind[i] <- BinarySearch(in A[1..m] for A[j]) - m + j
	sync
 
	# place each item in their ordered location
	parallel for i=1 to n
		B[Ind[i]] <- A[i]
	parallel for i=1 to n
		A[i] <- B[i]
	

• Span $O(\log n)$

then we have… alg. Parallel Merge Sort

def PMergeSort(A[1..n])
	# base case
	if n > 1
		m = ceiling(n/2)
	spawn PMergeSort(A[1..m])
	spawn PMergeSort(A[m+1..n])
	sync
	PMerge(A[1..m],A[m+1..n])

• Span $T_{\infty }(n)\le T_{\infty }\left(\frac{n}{2}\right)+O(\log n)=O({\log }^{2}n)$
• Work $W_{\infty }\le 2W_{\infty }\left(\frac{n}{2}\right)+O(n\log n)=O(n{\log }^{2}n)$
  • Second term is work done by parallel merge procedure: correctly placing $n$ items, each takes $O(\log n)$.

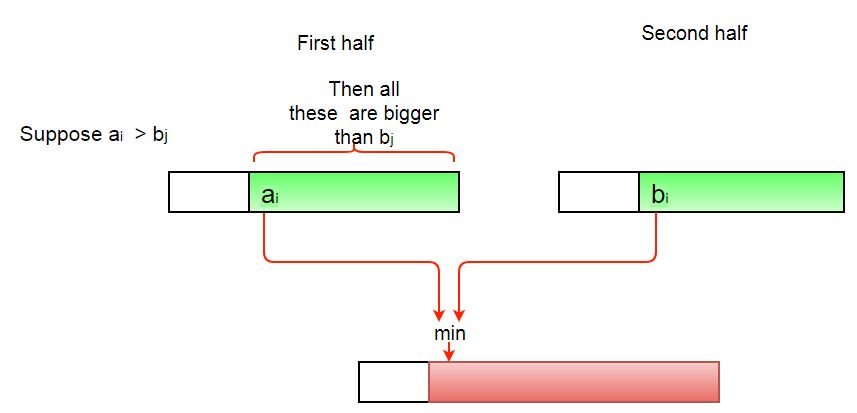
alg. Inversion Counting. In an unsorted array $A[\mathrm{1..}n]$ count how many pairs $A[i],A[j]$ are not in the correct order

• Idea: Mergesort, but during the merge step check how many times you need to reverse the pairs
• 

Partially Sorted §

Uses of partially sorted arrays:

• Top $k$ items: e.g. Google Search, College Admissions
• $k$-th largest/smallest item

$k$-th smallest item (=item of rank $k$) => use Tournament Tree