CS330 HW10

Problem 1 §

Algorithm is one that assigns every one element to the set with the smaller sum.

(a) §

1. We first establish that the cost of the algorithm $\text{ALG}={\sum }_{x\in S}x$ where $S$ is the bigger one of $A,B$.
   1. let $X=\{x_1\dots x_n\}$ where $x_i$ is the $i$-th processed element by $\text{ALG}$.
2. $\text{ALG}={\sum }_{x\in S}x-x_j+x_j$ where $x_j$ is the last item added to set $S$
   1. ! Looking at the first term, we can establish ${\sum }_{x\in S}x-x_j\le \frac{1}{2}({\sum }_{i<j}{x}_i$)……(1)
      1. i.e. $\text{Sum in S before }{x}_j\le \text{Average of total before }{x}_j$
      2. We know this because $\text{Sum in S before }{x}_j$ is the smaller sum of $A,B$, and thus the average is bigger than the minimum of the two.
   2. Then we also establish ${\sum }_{i<j}{x}_i\le {\sum }_{i<j}{x}_i+{\sum }_{i>j}{x}_i={\sum }_{x\in X}x-x_j$
      1. i.e. Sum before $x_i$ $\le$ sum before $x_j$ and sum after $x_j$ $=$ total sum excluding $x_j$
      2. ! This implies $\frac{1}{2}{\sum }_{i<j}{x}_i\le \frac{1}{2}\left({\sum }_{x\in X}x-x_j\right)$…….(2)
   3. & (1) and (2) together shows ${\sum }_{x\in S}x-x_j\le \frac{1}{2}\left({\sum }_{x\in X}x-x_j\right)=\frac{1}{2}\sum x-\frac{1}{2}{x}_j$……(3)
3. We thus show $ALG\le \frac{1}{2}\sum x-\frac{1}{2}{x}_j+x_j=\frac{1}{2}\sum x+\frac{1}{2}{x}_j$……(4)
   1. We know from the lecture (makespan, lemma 1 and 2) that $\frac{1}{2}\sum x\le OPT$ and $x_j\le OPT$
      1. first, because optimal solution cannot be smaller than the total / 2
      2. second, because optimal solution cannot be smaller than any element
   2. • Thus we establish $ALG\le OPT+\frac{1}{2}OPT=\frac{3}{2}OPT$
4. Thus proven

(b) §

1. We first investigate the trivial cases when $X$ has respectively $1,2$ and $3$ elements
   1. Case $n=1$
      1. $OPT=x_1$, $ALG=x_1$ thus $\alpha =1$
   2. Case $n=2$
      1. $OPT=max[x_1,x_2]$, $ALG=max[x_1,x_2]$ thus $\alpha =1$
2. We then investigate the case when $n\ge 3$
   1. As we also know that $x_1>x_2>x_3>\cdots >x_n$ in the order of assignment by $ALG$, we can state both that:
      1. $\frac{x_1+\cdots +x_i}{i}\ge x_i$ thus $x_1+\cdots +x_i\ge i{x}_i$……(1)
      2. $x_j\ge \frac{x_{i+1}+\cdots +x_n}{n-j}$ thus $x_j\ge x_{i+1}+\cdots +x_n$……(2)
      3. (1)$-$(2) yields ${\sum }_{k=1\dots i}{x}_k-x_j\ge$

Problem 2 §

Code §

import csv
from typing import List, Tuple
import time
from math import radians, cos, sin, asin, sqrt
import random
 
# Function to load data from CSV file
def load_data(riders_filepath) -> List[Tuple[float, float]]:
    passengers = []
    with open(riders_filepath, 'r') as file:
        csv_reader = csv.reader(file)
        next(csv_reader, None)  # Skip the header
        for row in csv_reader:
            sourceLat = float(row[1])
            sourceLon = float(row[2])
            passengers.append((sourceLat, sourceLon))
    return passengers
 
# Assuming the Haversine function is replaced by a simple Euclidean distance for this simulation
def euclidean_distance(point1, point2):
    return sqrt((point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2)
 
# 2-approximation algorithm for k-center clustering using Euclidean distance
def k_center_clustering_euclidean(passengers, k, n):
 
    # sample n elements from passengers
    passengers = random.sample(passengers, n)
 
    start_time = time.time()
 
    # Choose an arbitrary point as the first center
    hubs = [random.choice(passengers)]
    for _ in range(1, k):
        # Find the next hub as the point farthest from any existing hub
        next_hub = max(passengers, key=lambda p: min(euclidean_distance(p, hub) for hub in hubs))
        hubs.append(next_hub)
 
    end_time = time.time()
    
    # Assign each point to the closest hub and calculate the cost
    assignments = {hub: [] for hub in hubs}
    for passenger in passengers:
        closest_hub = min(hubs, key=lambda hub: euclidean_distance(passenger, hub))
        assignments[closest_hub].append(passenger)
 
    
    # The cost is the maximum distance of any point to its assigned hub
    cost = max(euclidean_distance(passenger, closest_hub)
               for closest_hub, passengers in assignments.items() for passenger in passengers)
    
    return hubs, assignments, cost, end_time - start_time
 
# Example passengers data (replacing the real CSV loading)
passengers = load_data("./passengers.csv")
print(len(passengers))
 
# Run the algorithm for different values of k and record the results
print("K")
results = {}
for k in range(50,200,10):
    hubs, assignments, cost, runtime = k_center_clustering_euclidean(passengers, k, 100)
    print(k, ",", runtime)
 
print("N")
for n in range(1000, 5000, 100):
    hubs, assignments, cost, runtime = k_center_clustering_euclidean(passengers, 10, n)
    print(n, ",", runtime)
 

Results §

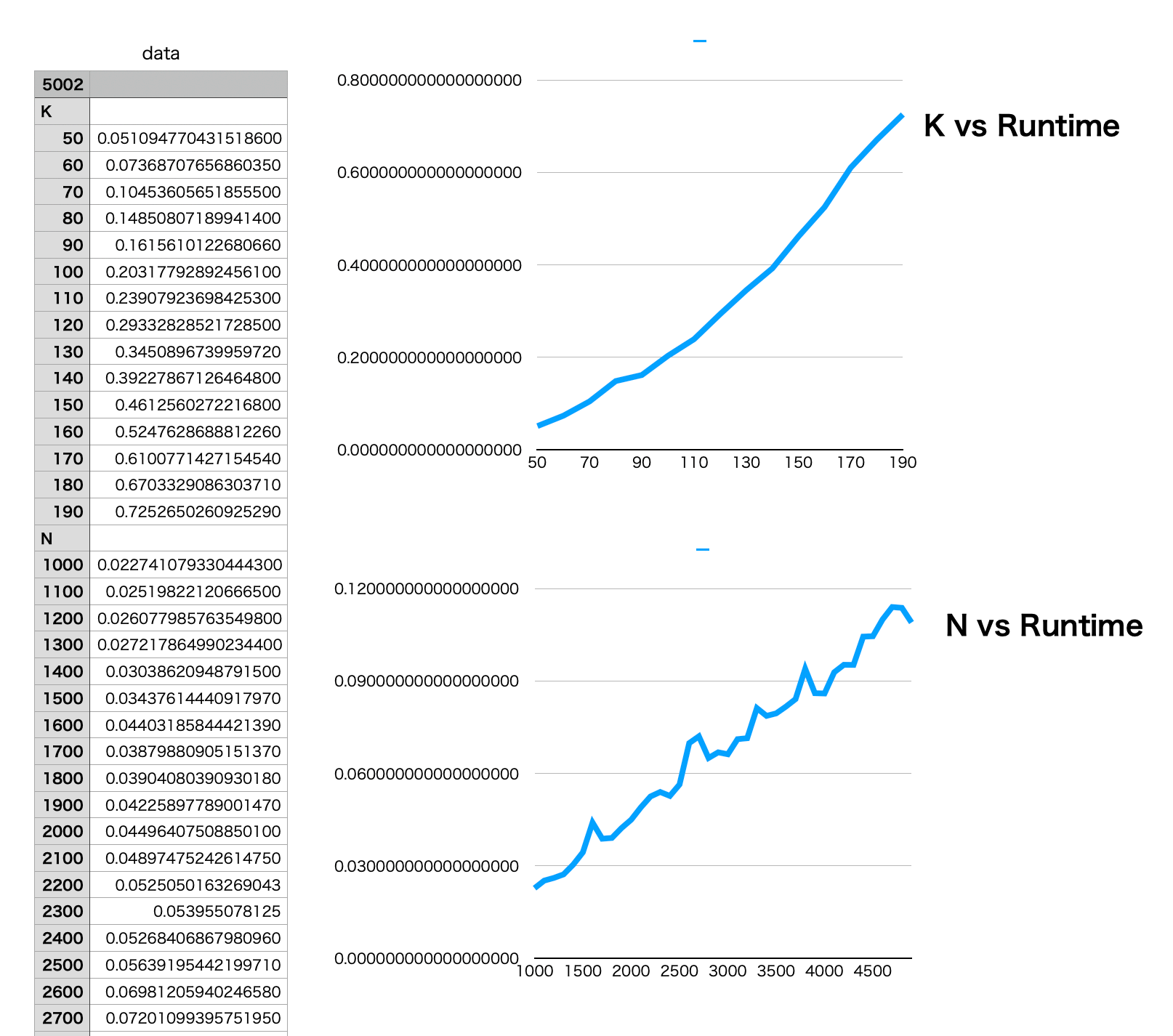
Problem 3 §

import csv
from typing import List, Tuple
import time
from math import sqrt
import random
import numpy as np
 
# Function to load data from CSV file
def load_data(riders_filepath) -> List[Tuple[float, float]]:
    passengers = []
    with open(riders_filepath, 'r') as file:
        csv_reader = csv.reader(file)
        next(csv_reader, None)  # Skip the header
        for row in csv_reader:
            sourceLat = float(row[1])
            sourceLon = float(row[2])
            passengers.append((sourceLat, sourceLon))
    return passengers
 
# Euclidean distance function
def euclidean_distance(point1, point2):
    return sqrt((point1[0] - point2[0]) ** 2 + (point1[1] - point2[1]) ** 2)
 
# Function to initialize centroids randomly
def initialize_random(passengers, k):
    return random.sample(passengers, k)
 
# Function to initialize centroids using k-means++
def initialize_kmeans_plusplus(passengers, k):
    centroids = [random.choice(passengers)]
    # probabilistic initialization
    for _ in range(1, k):
        distances = [min(euclidean_distance(p, c) for c in centroids) for p in passengers]
        probabilities = [d ** 2 for d in distances]
        total = sum(probabilities)
        probabilities = [p / total for p in probabilities]
        next_centroid = random.choices(passengers, weights=probabilities, k=1)[0]
        centroids.append(next_centroid)
    return centroids
 
# Assign passengers to the nearest centroid
def assign_passengers(passengers, centroids):
    assignments = {}
    for passenger in passengers:
        closest_centroid = min(centroids, key=lambda centroid: euclidean_distance(passenger, centroid))
        if closest_centroid in assignments:
            assignments[closest_centroid].append(passenger)
        else:
            assignments[closest_centroid] = [passenger]
    return assignments
 
# Update centroids based on the mean of assigned points
def update_centroids(assignments):
    centroids = []
    for points in assignments.values():
        centroids.append(tuple(np.mean(points, axis=0)))
    return centroids
 
# Calculate the quality of solution
def calculate_quality(assignments):
    total_distance = 0
    for centroid, points in assignments.items():
        total_distance += sum(euclidean_distance(centroid, p) ** 2 for p in points)
    return total_distance / len(assignments)
 
# k-means algorithm
def k_means(passengers, k, initialize_func):
    # Initialize centroids
    centroids = initialize_func(passengers, k)
    assignments = {}
    for _ in range(20):  # fixed number of iterations for simplicity
        # Assign passengers to the nearest centroid
        assignments = assign_passengers(passengers, centroids)
        # Update centroids
        centroids = update_centroids(assignments)
    return centroids, assignments
 
# Run the k-means algorithm with different initializations
def run_k_means(passengers, k_values):
    results = {k: {'random': int, 'k-means++': int} for k in k_values}
    for k in k_values:
        for _ in range(3):  # Repeat the experiment 3 times
            temp_results = {init: {'runtime': 0, 'quality': 0} for init in ('random', 'k-means++')}
            for init, func in [('random', initialize_random), ('k-means++', initialize_kmeans_plusplus)]:
                start_time = time.time()
                centroids, assignments = k_means(passengers, k, func)
                runtime = time.time() - start_time
                quality = calculate_quality(assignments)
                temp_results[init]["runtime"] += runtime
                temp_results[init]["quality"] += quality
        # average the results
        results[k]['random'] = (temp_results['random']['runtime'] / 3, temp_results['random']['quality'] / 3)
        results[k]['k-means++'] = (temp_results['k-means++']['runtime'] / 3, temp_results['k-means++']['quality'] / 3)
    return results
 
# Example passengers data (replacing the real CSV loading)
# Here we need to load the data from the file provided by the user
# passengers = load_data("/path/to/passengers.csv")
 
passengers = load_data("./passengers.csv")
print(len(passengers))
 
# Define k values to test
k_values = [2, 4, 6, 8]
 
# Run the k-means algorithms and print the results
results = run_k_means(passengers, k_values)
print(results)
 

Results §

Number of Clusters	Initialization	Runtime	Quality
2	random	0.09817	2.26508
2	k-means++	0.09790	2.26508
4	random	0.15675	0.77163
4	k-means++	0.15921	0.72164
6	random	0.20530	0.39536
6	k-means++	0.21513	0.35047
8	random	0.26586	0.23331
8	k-means++	0.28957	0.20059