Revenue-Maximizing Auctions

Motivation. Sometimes we aim to maximize revenue instead of social welfare.

• In this case, we assume that we know a little bit about the bidder’s private valuations—we know the distributions $v_i\sim F_i$. (we call this a baysian auction.)
  • This is because unless we do this, the revenue maximization is impossible, since it is hard to guarantee DSIC.)
• Then, in a DSIC auction $M=(x(\vec{b}),p(\vec{b}))$, the revenue maximization goal can be phrased as:

$${\text{max}}_{x,p}\mathbb{E}\left(\sum _{\forall i}{p}_i(\vec{v})\right)$$

In order to do to this, we introduce a new concept, and as we will see later it will simplify the above problem.

def. Virtual Value. For a bidders’ true valuation $v_i$ whose CDF is $F_i(v_i)$, PDF is $f_i(v_i)$, the virtual value is defined as:

$$\phi (v_i):=\underset{\text{ want to collect }}{\underbrace{v_i}}-\underset{\text{ information penalty }}{\underbrace{\frac{1-F_i(v_i)}{f_i(v_i)}}}$$

Properties.

• $\phi (v_i)\le v_i$
• $\phi (v_i)$ may be negative

Intuition. As annotated above, treat $v_i$ as the amount of money we would like to collect from bidder $i$. But this is discounted by a certain factor (=“information penalty”) because we know a bit of information about them—their distribution.

We can rephrase the above revenue maximization problem in terms of virtual value as the following:

thm. (expected virtual welfare is expected revenue)

$$\mathbb{E}\left(\underset{\text{ revenue }}{\underbrace{\sum _{\forall i}{p}_i(\vec{v})}}\right)=\mathbb{E}\left(\underset{\text{ virtual welfare }}{\underbrace{\sum _{\forall i}{\phi }_i(v_i)x_i(\vec{v})U}}\right)$$

Motivation. Now the revenue maximization goal is simply to maximize expected virtual welfare. However, we still need to make sure the bidders are truthful, because we need to maximize over $\vec{v}$.

• ⇒ Using Myerson’s lemma, we can create auctions that are truthful. The following are conditions of Myerson’s lemma, applied in the context of virtual value.
• Then, we will give an example of this in a single-item many-bidder auction where these conditions hold.

def. Vickery Auction with Reserve

1. Calculate virtual values ${\phi }_1,\dots ,{\phi }_n$ for all bidder’s bids $b_1,\dots ,b_n$
2. Give the item to the bidder with the highest virtual value ${\phi }_1$, unless the highest bidder’s virtual value is below zero—${\phi }_1<0$.
   1. The the highest bidder’s virtual value is below zero, throw away the item. Auction is over.
3. Calculate the reserve price $r:={\phi }^{-1}(0)$
4. Charge them $\text{max}(v_2,r)$—either the reserve price, or the second-price
5. This auction will maximize revenue.

Visual Interpretation. An example of three different cases where different distributions lead to different virtual value

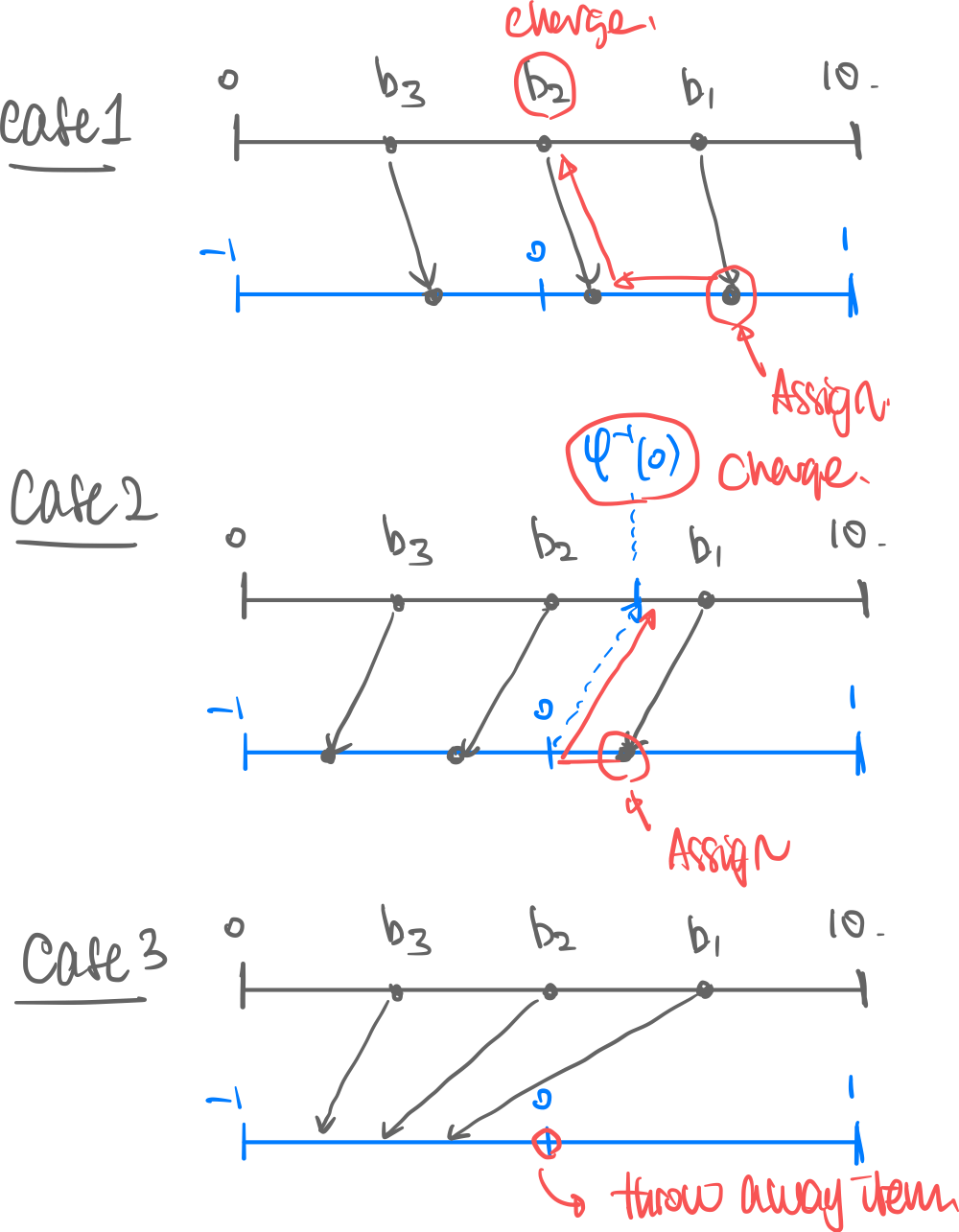
thm. (General case of revenue maximization.)

• Assuming $F_i$ is regular for every bidder $i$…

1. Transform the truthfully reported valuation $v_i$ into corresponding virtual value ${\phi }_i(v_i)$
2. Allocate by maximizing virtual welfare: $x(\vec{v})={\text{argmax}}_X{\sum }_{\forall i}{\phi }_i(v_i)\cdot x_i$
3. Charge payments $p(\vec{v})$ according to the

def. Regular Distribution. A distribution is regular iff if its virtual value function is monotonic.

thm. If all bidder’s values follows an i.i.d. regular distribution, Vickery Auction with Reserve is DSIC.