Nash Equilibrium

def. Nash Equilibrium is a set of strategies (one for each player) which is the best response strategy of each other’s move; i.e. you can’t deviate without destabilizing the equilibrium

alg. Finding the Nash Equilibrium in a payoff matrix. Corner Method to find NE in payoff matrix. 1. For each player: 2. For each other player’s move; highlight the line of the best response → When both the left and top lines are highlighted that is NE.

Pure Strategy Nash Equilibirum §

def. PSNE. $\vec{s}=(s_1,s_2)$ is PSNE for two players $1,2$ iff:

$$\begin{array}{rl}{s}_1& ={\text{argmin}}_{s\in S_1}{c}_1(s,s_1)\\ s_1& ={\text{argmin}}_{s\in S_2}{c}_2(s_1,s)\end{array}$$

How to Find NE §

• In Simultaenous Games: Use the Corner method
• In Sequential Games: Make the Decision Tree into a Payoff Matrix, and use the Corner method:

e.g. Driving left or Right

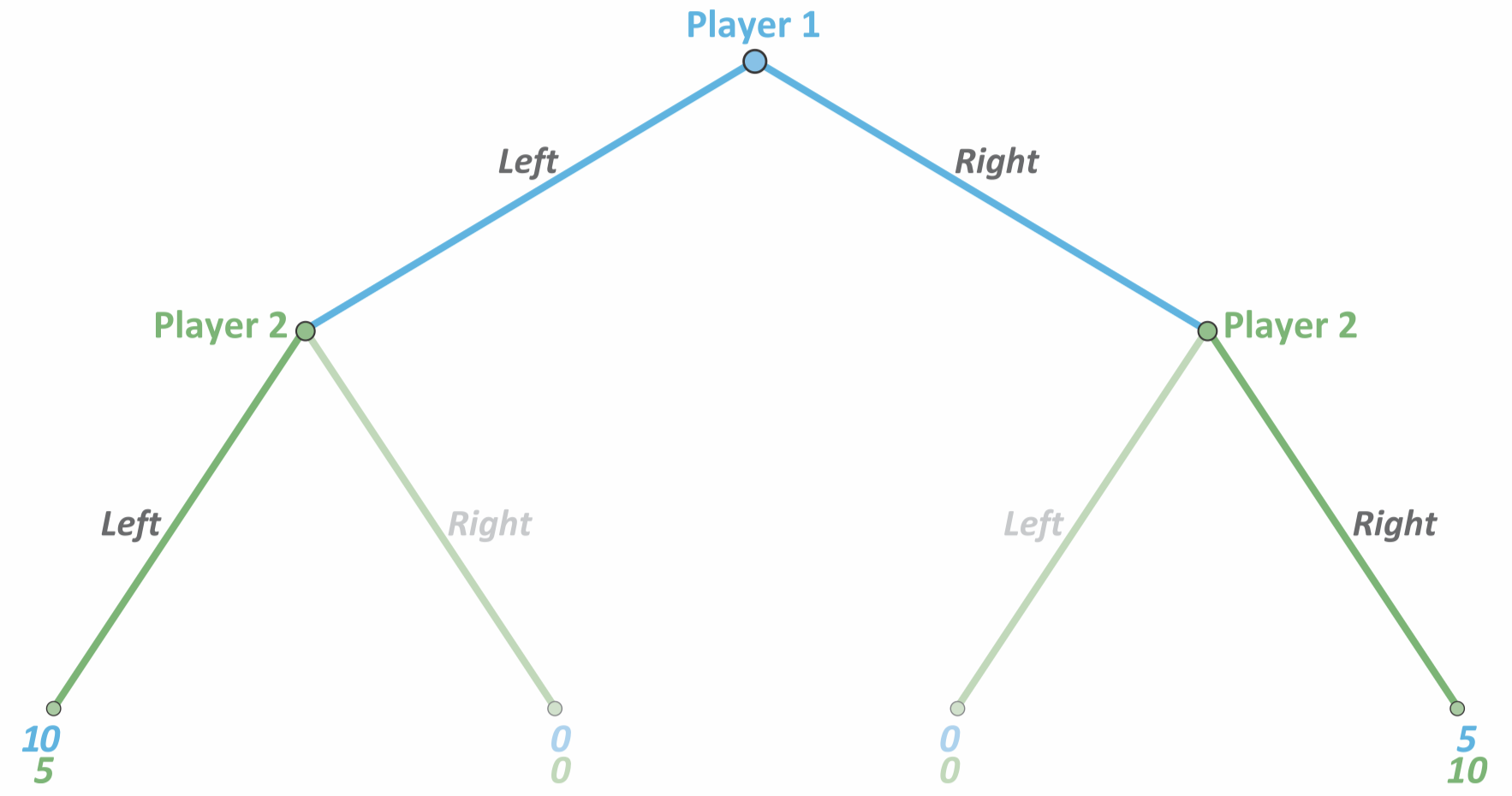
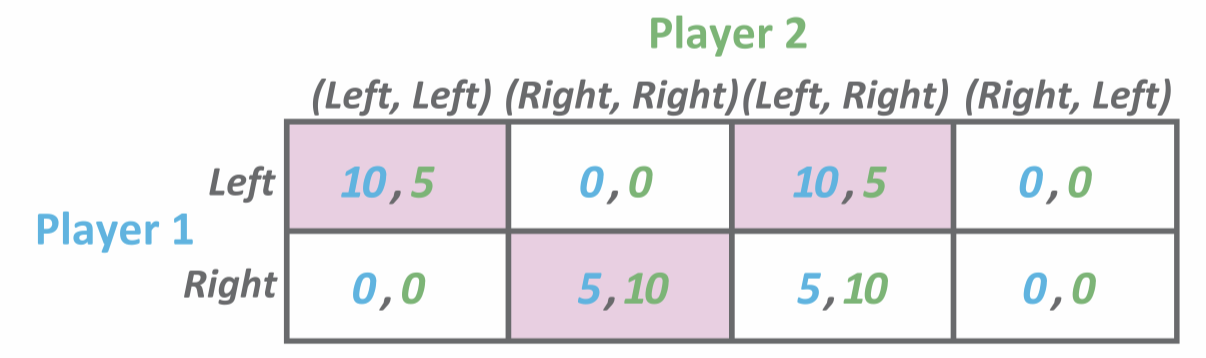
Subgame Perfect Nash Equilibrium (SPNE) §

def. A Non-credible threat is when the follower in a sequential move game says: “If I can’t win, I’ll take you down no matter how much it costs to me.”

• In the above game, $(R,R)$ is an example of a non-credible threat because when Player 1 chooses L, Player 2’s best response is L—but Player 2 threatens to go R. This is because they want the best possible outcome for them, $R,(R,R)$

def. Subgame Perfect Nash Equilibria (SPNE) are NE where the follwer will only choose strategies that are best for them, and can’t threaten the leader beforehand with non-credible threats.

To find the SPNE of a game, use Backwards Induction:

1. Determine the last player’s best strategy
2. The second-last player knows what the last player will do. Then determine what the second-last player will do.
3. Continue solving until the first player.

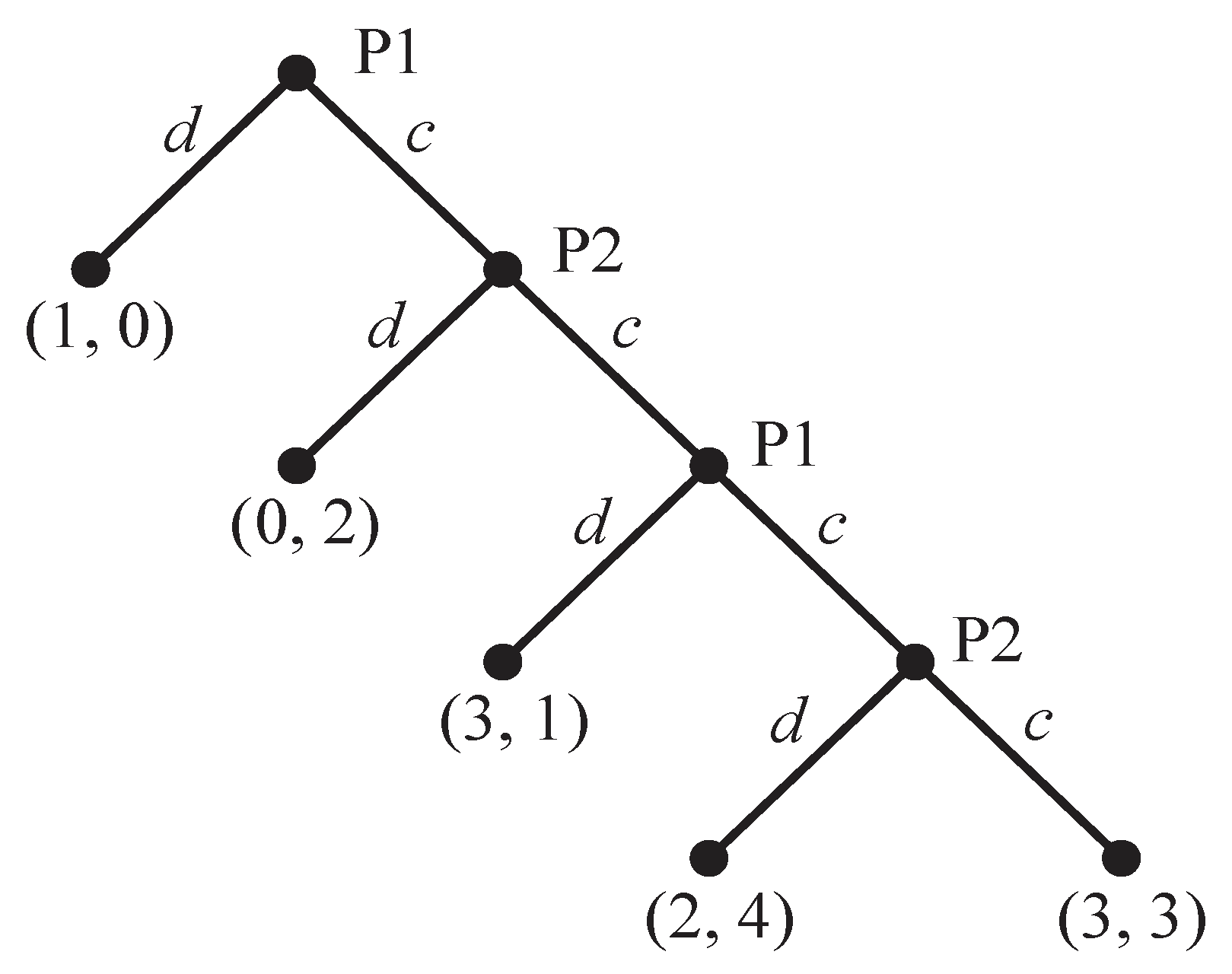
$SPNE=\{(d,d),(d,d)\}$, payoff is (1,0) which is a lot worse off that global optimal.