Matrix Multiplication

Traditional (Textbook) algorithm is $O(n^3)$ We have gotten it down to $\approx O(n^{2.37})$

alg. PInnerProduct. Use PSum from Parallel Algorithmss. Calculates Inner Product of two vectors

• Span $T_{\infty }(n)=O(\log n)$
• #processors $p=O\left(\frac{n}{\log n}\right)$
• Work: $W_{\infty }(n)=O(n)$

alg. Matrix Multiplication.

• $T(n)=O(n^3)$

def MatMult(A, B)
	for i=1 to n
		for j=1 to n
 
			# calculate inner product
			c_ij = 0
			for k=1 to n
				c_ij += a_ik * b_jk
			end for
		end for
	end for

alg. Parallel Matrix Multiplication.

def PMatMult(A, B)
	parallel for i=1 to n
		parallel for j=1 to n
			c_ij = 0
			for k=1 to n
				c_ij += a_ik * b_jk
			end for
		end for
	end for

alg. Parallel Recursive Matrix Multiplication. A Divide-and-Conquer algorithm.

Idea:

$$C=\left(\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right),A=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right),B=\left(\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right),$$ $$\left(\begin{array}{cc}{C}_{11}& C_{12}\\ C_{21}& C_{22}\end{array}\right)=\left(\begin{array}{cc}{A}_{11}& A_{12}\\ A_{21}& A_{22}\end{array}\right)\left(\begin{array}{cc}{B}_{11}& B_{12}\\ B_{21}& B_{22}\end{array}\right)=\left(\begin{array}{cc}{A}_{11}{B}_{11}+A_{12}{B}_{21}& A_{11}{B}_{12}+A_{12}{B}_{22}\\ A_{21}{B}_{11}+A_{22}{B}_{21}& A_{21}{B}_{12}+A_{22}{B}_{22}\end{array}\right)$$

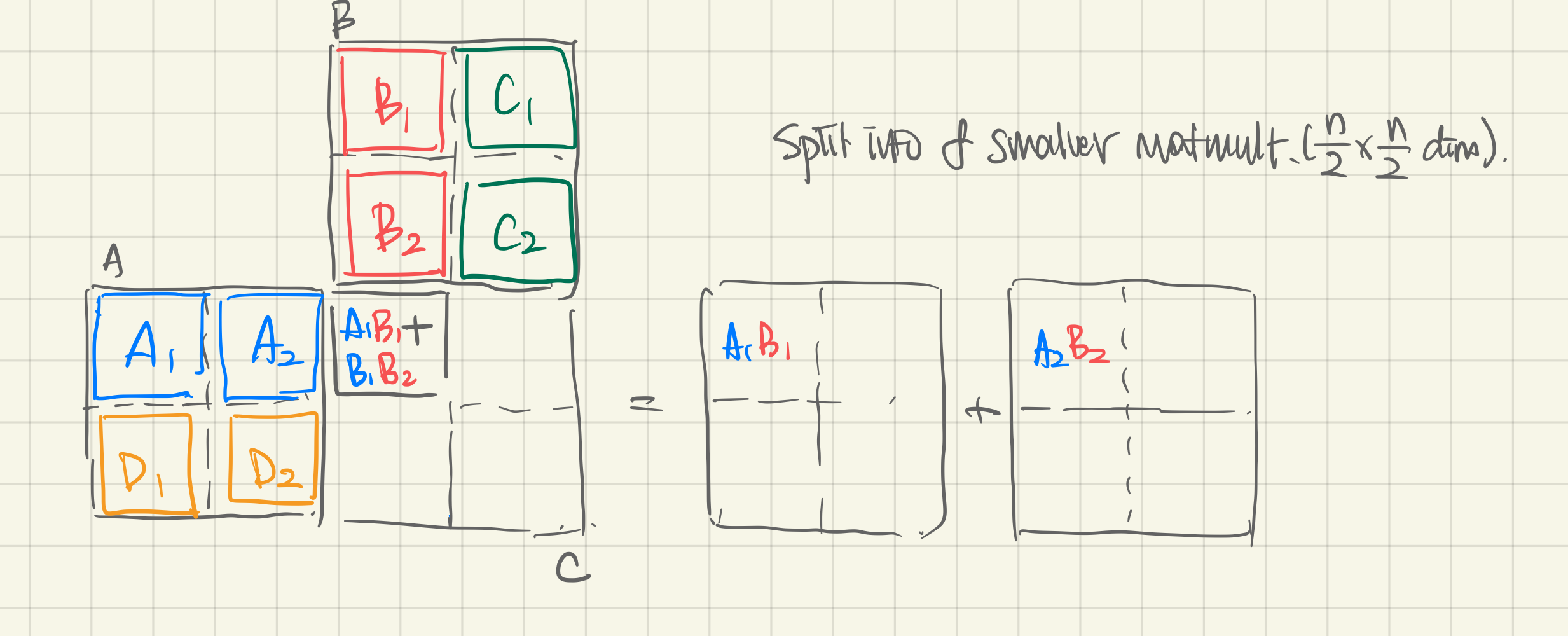
def PRMatMult(A, B, C)
 
	# base case
	if n=1
		return a * b
		
	# parallel recursion
	spawn PRMatMult(A_11, B_11, D_11)
	...# 8 parallel threads
	spawn PRMatMult(A_22, B_22, E_22)
	sync
 
	# add matricies D and E together
	parallel for i=1 to n
		parallel for j=1 to n
			c_ij = d_ij + e_ij

• Span $T_{\infty }(n)\le T_{\infty }\left(\frac{n}{2}\right)+O(1)=O(\log n)$
• Work $W_{\infty }(n)\le 8\cdot W_{\infty }\left(\frac{n}{2}\right)+O(n^2)=O(n^3)$