Assume the Efficient Market Hypothesis.
Info
How to maximize returns while minimizing risk [=volatility =std. dev.]? → Since risk/return is proportional to each other, you choose one optimization goal.
- Single Stock (See Dividend Discount Model)
- Price of stock at time :
- Return of stock at time :
- are all Random Variables
- Expected Return of stock :
- Volatility (=Risk) of Stock :
Two-stock Portfolios
- Covariance of stocks :
- Correlation of stock : such that
- Weights for
- Portfolio Expected Return:
- Portfolio Variance:
- Minimum Variance Portfolio:
N-Stock Portfolio
- Known information: are all known
- Multiple Stocks (=Portfolio)
- Position of portfolio at time (=amount invested):
- Portfolio Return at time
- Portfolio Expected Return at time :
- Portfolio Variance:
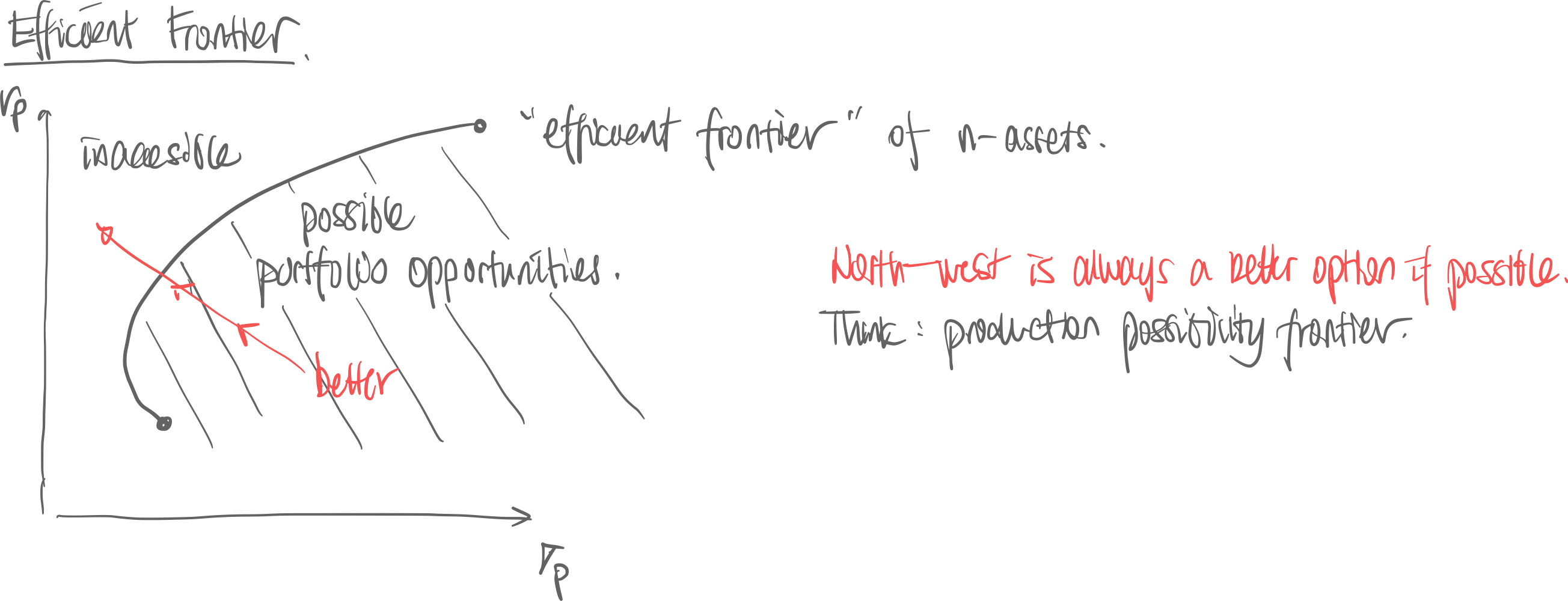
def. Feasible Portfolios. Set of tuples given we have many assets weighted .
- ← Short-selling is allowed
- Lower the correlation [= the more negatively correlated] the better diversification is.
- When two stocks have perfectly negative correlation , the efficient frontier touches the -axis (=)
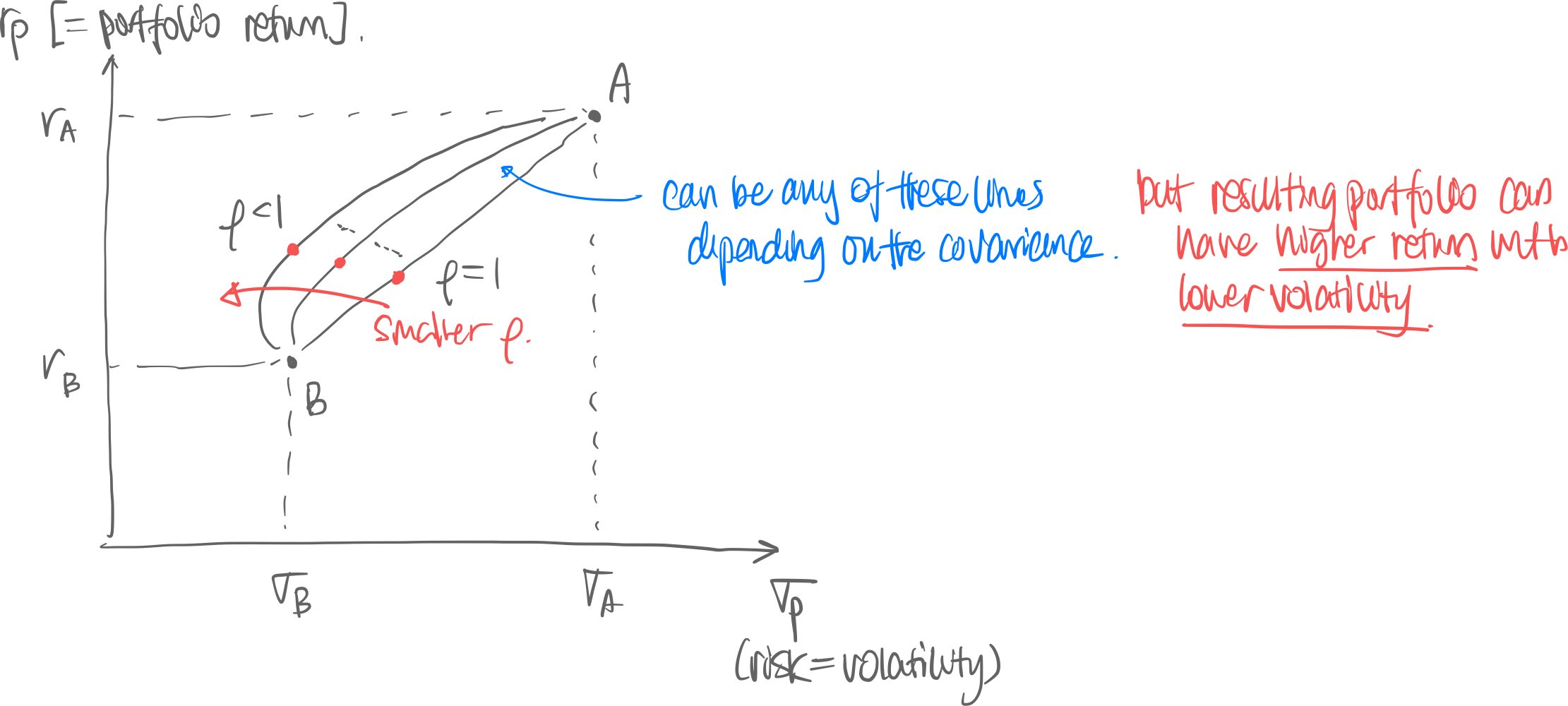
- When two stocks have perfectly negative correlation , the efficient frontier touches the -axis (=)
Efficient Frontier
- “Minimize the variance such that the sum of weights are and the portfolio return is (a constant)”
- Key Assumption: neither the returns or risks are identical, and there is no perfect correlation
- Minimum for given return level at:
- Efficient Frontier:
- …where are scalars: