Computational Tractability

Definitions §

thm. Satisfiability Reducibility. All problems can be reduced to boolean satisfiability problems.

• Optimization problems: choose some $k$, then ask “is there a solution $\le k$?, $\ge k$?” => Then do a binary search on $[0,k]$ or $[k,\text{upper bound}]$

def. Computationally tractable problems. There exists a polynomial time algorithm $O(n^k)$ for the solution. The set of all computationally tractable problems is denoted $P$.

• Most problems in CS 330 Advanced Algorithms

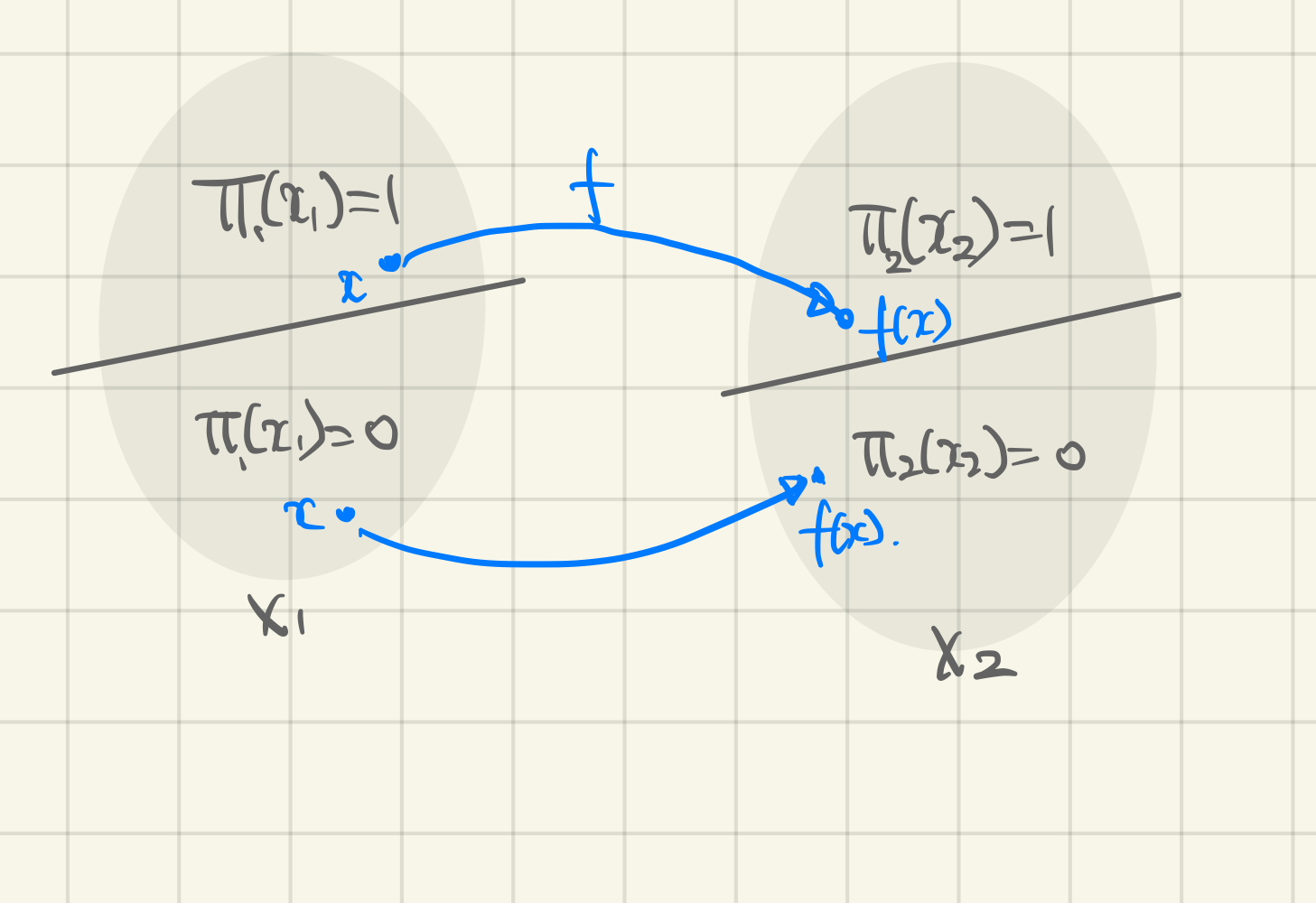
thm. Polynomial Reduction. Problem ${\pi }_1:X_1\mapsto \{0,1\}$ that is an element of $P$ can be reduced to problem ${\pi }_2:X_2\mapsto \{0,1\}$ problem which is also in $P$, if there exists a function $f:X_1\mapsto X_2$ such that:

1. ${\pi }_1(x_1)=1⟺{\pi }_2(f(x_1))=1$
2. $f(x)$ takes polynomial time to complete
   1. $f(x)$ can be a many-to-one function

• This is denoted ${\pi }_1{\le }_p{\pi }_2$
• Visually:
• Implications of when ${\pi }_1{\le }_p{\pi }_2$
  • ${\pi }_2$ is at least as hard as ${\pi }_1$.
  • P-time:
    • If ${\pi }_2$ is a P-time problem and
    • ! If the input size to ${\pi }_2$ which is $|f(x)|$ is bounded by $|x{|}^c$
    • Then ${\pi }_1$ is also a P-time problem
  • NP-hardness:
    • If ${\pi }_1$ is NP hard → ${\pi }_2$ is also NP-hard
• & Techniques for reduction of ${\pi }_1{\le }_p{\pi }_2$
  • Process:
  1. If ${\pi }_1,{\pi }_2$ is a min/maximization problem, convert it to a decision problem
  2. If construction is needed, construct from ${\pi }_1$ to ${\pi }_2$: domain $G\to G^{\prime }$
     1. ! The construction may not suppose you know the answer ${\pi }_1$.
     2. If it’s a graph, it should apply to any graph
     3. If it’s a set, it should apply to any set
     4. • If there is something like “exists solution of size $k$” in ${\pi }_1$, this $k$ will probability be present in ${\pi }_2$ as well
  3. Prove that if $\exists$ answer to ${\pi }_1$ in domain $G$, that implies $\exists$ answer to ${\pi }_2$ in domain $G^{\prime }$.
  4. Prove that if $\exists$ answer to ${\pi }_2$ in domain $G^{\prime }$, that implies $\exists$ answer to ${\pi }_1$ in domain $G$.
  5. Proven!

Complexity Classes §

Complexity classes are an extension of the Chompsky Heirarchy.

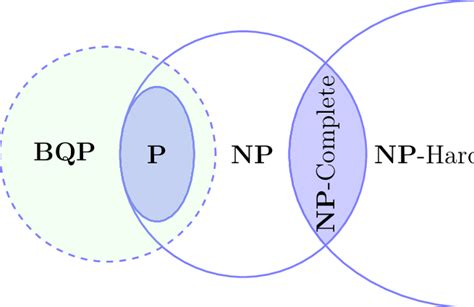
1. P (Polynomial Time)
2. NP (Nondeterministic Polynomial Time) The certificate exists that can be verified in polynomial time. A non-deterministic Turing Machine can solve it in polynomial time because it has many paths.
3. co-NP
   • problem $\pi \in \text{NP}⟹{\pi }^c\in \text{co-NP}$:luc_check_circle:
   • problem $\pi \in \text{NP}⟺\pi \in \text{Co-NP}$ is an open problem See Whats the difference between NP and co-NP - Stack Overflow
4. NP-complete: Problems where any NP problem can be reduced into in polynomial time.
   1. If there is any NP-complete problem that can be shown to be solved in polynomial time, then P=NP.
   2. thm. Cook-Levin Theorem. CNF-SAT is NP-complete.
   3. & To prove a decision problem $\pi$ is NP-complete
      1. Show $\pi \in NP$ i.e. certificate can be checked in poly-time
      2. Show ${\pi }_0{\le }_p\pi$ where ${\pi }_0$ is known NPC problem by…
         1. from solution $I_0$ of ${\pi }_0$, construct solution $I$ of $\pi$
         2. show that $I_0$ is solution for ${\pi }_0$ if and only if $I$ is solution for $\pi$ (both ways needed to show that non-solutions are non-solutions)
   4. “Completeness” can apply to any complexity class. It means that it is the “hardest” problem in that class.
5. NP-hard: Problems that are at least as hard as all NP (and NP-complete) problems
   1. Equivalently, Problems that are as hard or harder than all NP problems

List of Problems and Reductions §

NP-Complete Problems §

• CNF-SAT (Cooke-Levin Theorem)
• 3-SAT
• Independent Set Problem
• Common Graph Problems Problem
• Subset Sum Problem
• Common Graph Problems
• Traveling Salesperson Problem
  • Cycle

Karp’s 21 NP-complete problems - Wikiwand Category:NP-complete problems - Wikipedia (DevonThink) NP-complete Reductions