Motivation. As opposed to Fractional Allocation where an item can be infinitely divided (and thus much fairness criteria are satisfied), in a situation where you cannot divide the items it is much harder to find a “fair” allocation. We will try nevertheless; here are a few attempts:
- Converting fraction allocation to integer allocation
- Serial Dictatorship
- Nash Welfare Objective
\mu_{i}is an additive utility function.
Fractional to Integer
First use fractional, then convert to integer allocation.
Serial Dictatorship
def. Serial Dictatorship. (Round Robin). The following process of allocation is a SD allocation:
- Round : Each agent picks favorite item
- Repeat until all items allocated Properties.
- SD is EF1 (defined and proved below)
- SD is not PO
- Comparable to MMS (bounded; see below) def. Envy-Free without one item (EF1). An allocation is envy-free without one item if:
Intuition. If envies ’s basket (=traditional Envy) then take out one item , and then no longer envies .
thm. SD is EF1. Proof. For all agent , let’s say envies .
- Due to SD game order, ’s pick in the -th round will always be preferred to ’s pick in the -st round. Therefore, will:
- The issue arises because may pick before in round . If we simply remove that item, will not envy anymore.
- Therefore, in any pair of agents envying , removing one item that was picked by before in the first round is enough to make no longer envy . ■
Example.
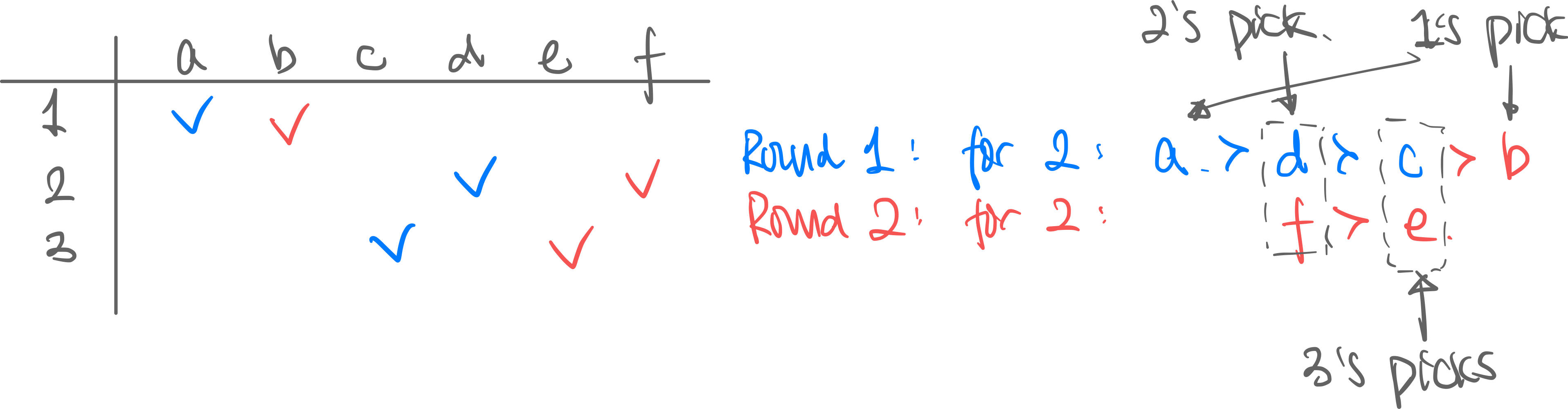
- may envy because prefers to , its first pick.
- But does not envy any other of ’s pick, because it picked it.
- Removing from ’s set makes no longer envy .
Comparison to MMS
def. Maximin Share (MMS). Imagine first an allocation process where
- splits the items first
- All other agents chooses which item to have
- gets the remaining item. In this case, it is in ’s best interest to maximize the minimum utility bundle (for itself)‘s utility. Thus we have the definition of MMS as the utility of this maximin bundle:
Example. The blue groups are what each agent splits the items into to maximize their minimum utility. The red circles are an example allocation that give more utility than MMS for every agent. 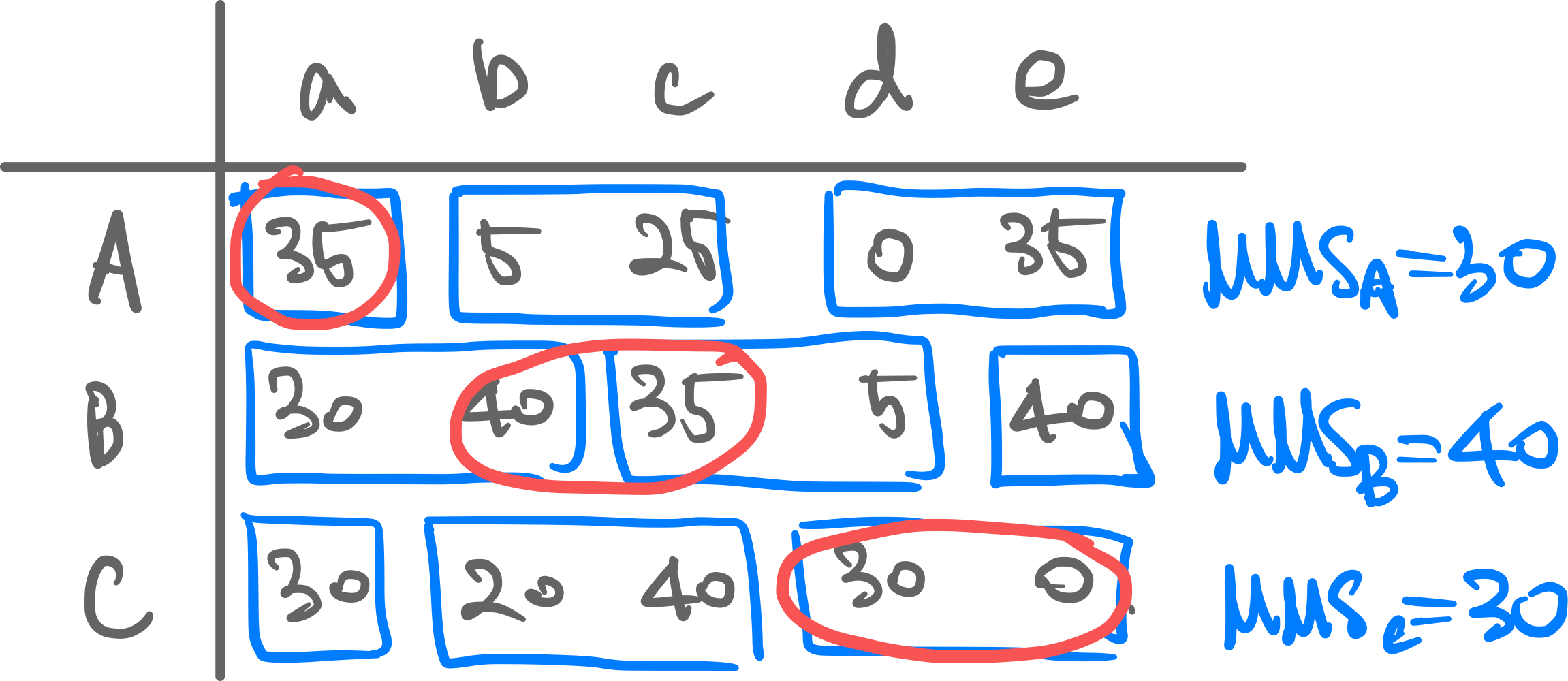 lem. (MMS utility worse than proportional utility). If we allow a fractional allocation on items , a proportional allocation will give utility for agent . On the other hand, if you use (integer) MMS allocation:
lem. (MMS utility worse than proportional utility). If we allow a fractional allocation on items , a proportional allocation will give utility for agent . On the other hand, if you use (integer) MMS allocation:
Therefore we ■
thm. (Serial Dictatorship vs. Proportional vs. MMS) Let be a serial dictatorship allocation. For agent , let be a single item that values the most. Then:
Proof. Model the round robin with agents and items from set , s.t. we call round 1 starting with agent . All items allocated before in round 1, let . These are ignored for now.
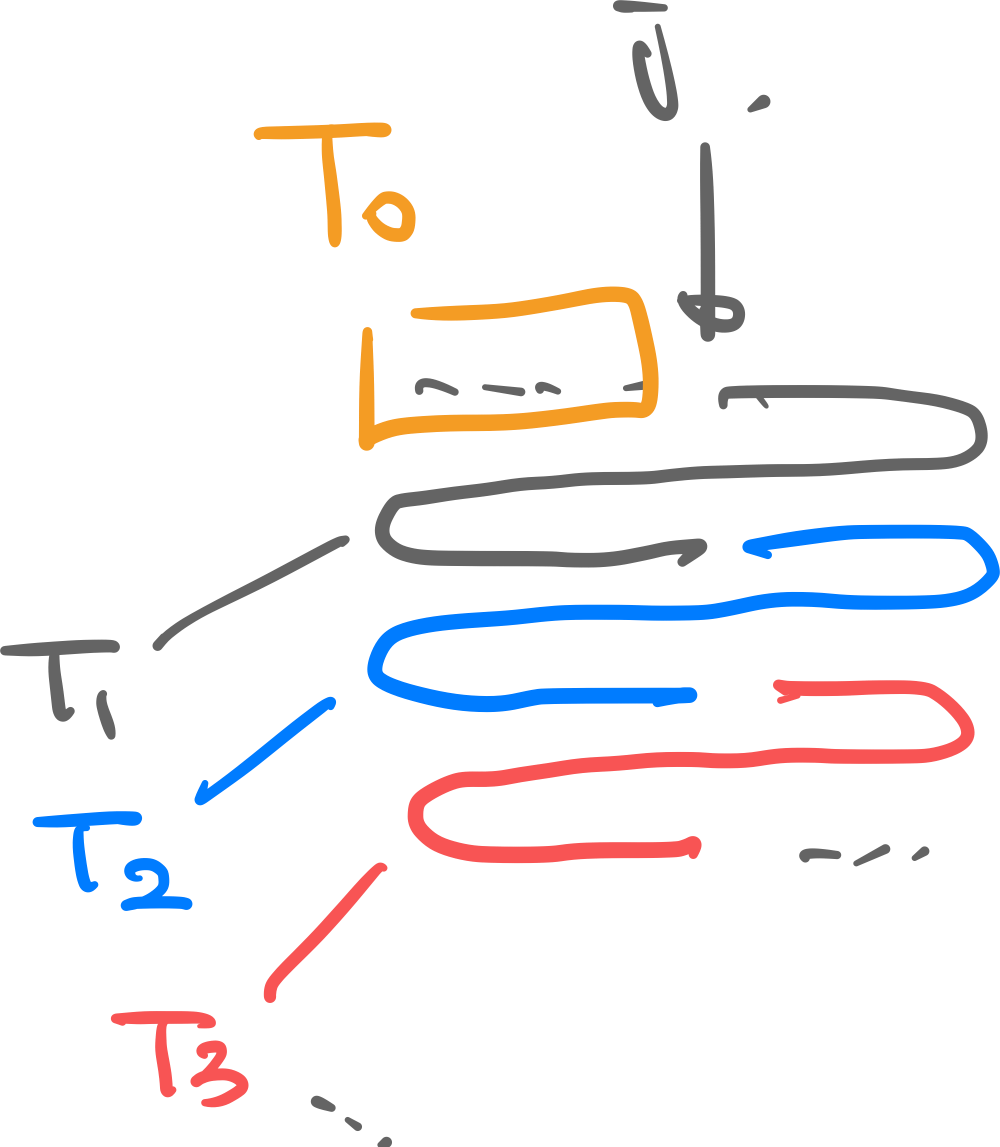 Let the items allocated to agents in round be . Let be the utility to agent by the single item allocated to on round . For agent in every round:
Let the items allocated to agents in round be . Let be the utility to agent by the single item allocated to on round . For agent in every round:
Now, consider the ignored items . We can easily establish that:
Continuing on from above:
Thus we have the final inequality w.r.t proportional allocation and thus MMS (due to theorem before).
■
thm. (Alternative SD vs MMS) Serial Dictatorship allocation satisfies for each agent that:
Proof.
■
Integer Nash Welfare
def. Integer Nash Welfare. For integer allocation , Nash welfare is:
- NP hard to compute
- …but satisfies EF1
thm. (Integer Nash Welfare objective satisfies EF1). Proof. Suppose in the allocation , envies even remove one item. Now, choose as the most bang-for-buck item to move from to :
And we also note the inequality (1):
Now per our assumption, still envies :
Now, on the other hand, since are NW allocations, it is the maximum product:
■