Controlled Experiments

Motivation. In theory we should be able to estimate the causal effect of a controlled experiment using Difference of Means model:

$$Y_i={\beta }_0+{\beta }_1\text{isTreated}+{ϵ}_i$$

But we have the following issues in really (ABC issues):

• Attrition
• Balance
• Compliance

Balance §

• def. Balance means treatment and control groups are same in all other factors
• def Blocking means to categorize into blocks (e.g. men and women) and randomize within groups.
  • Blocking is harder to implement when there are lots of categories, and sample size is limited. Therefore, before running regression check for balance by running the Balance Test:

$$X_i={\gamma }_0+{\gamma }_1\underset{\text{ isAssigedTreatment }}{\underbrace{Z_i}}+{\nu }_i$$

where $X_i$ is a covariate that we’re worried is not randomized enough.

• 😊 If ${\gamma }_1$ is not statistically significant, it means treatment and unobserved factors are not correlated.
• 😞 If ${\gamma }_1$ is statistically significant then (even if it was randomized) then ${\rho }_{T,ϵ}\ne 0$ it’s a failure of randomization

Compliance §

Motivation. Some people don’t comply, even through they’re offered treatment. What if people who don’t comply are different from people who comply? If this is the case, then focussing on just the treated & compliant people would be not indicative of the true effect of the treatment.

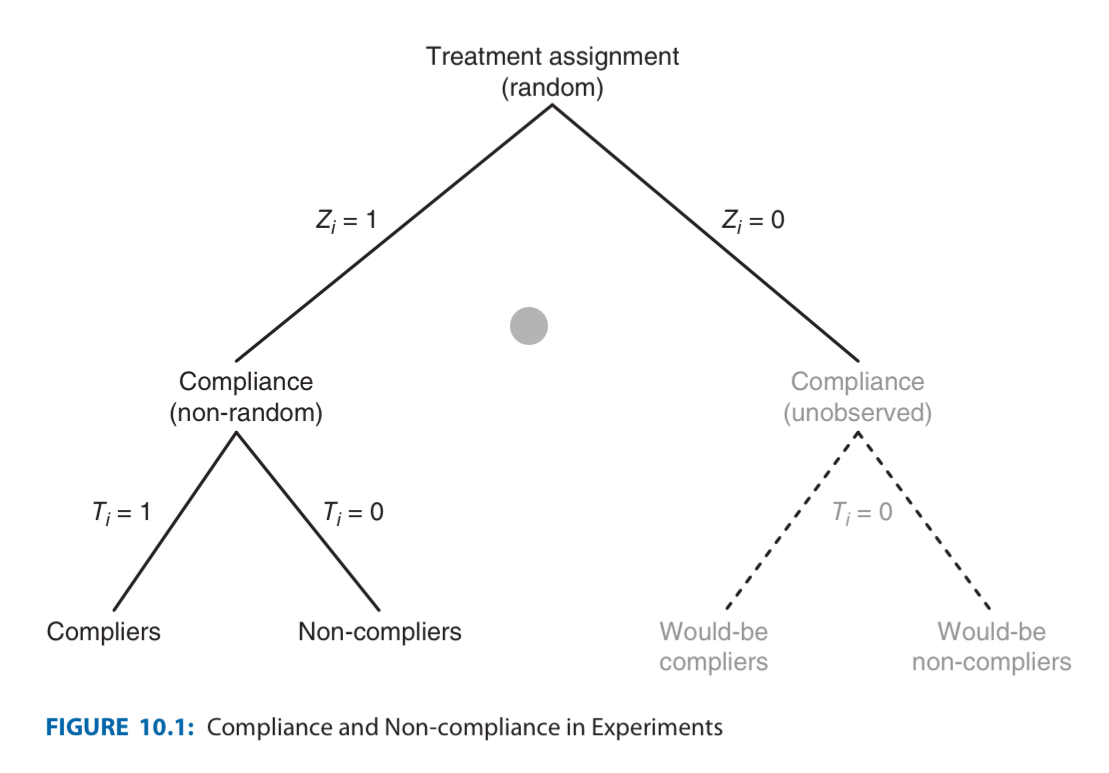
• $Z$ is the binary “was going to treat this person”
• $T$ is the binary “is compliant person”

Intention to Treat Approach §

We attempt to resolve this issue by not regressing against treated & compliant people, but all people who were “supposed to be treated” (=intent to treat), i.e. $T=1\wedge Z=1$

• Non-ITT: $Y_i={\beta }_0+{\beta }_1\underset{\text{ hasComplied }}{\underbrace{T_i}}+{ϵ}_i$
• ITT: $Y_i={\delta }_0+{\delta }_1\underset{\text{ ITT }}{\underbrace{Z_i}}+{\nu }_i$
  • This is a conservative estimate. $|{\delta }_1|\le |{\beta }_1|$; the lower the compliance, the lower the coefficient. (Full compliance implies ”$=$“)

2SLS Approach §

Alternatively, a better approach to dealing with non-compliance is using a 2SLS. You can use the ITT variable $Z$ as the IV, since it satisfies the conditions that make a good IV:

• Inclusion condition: $Z$ is correlated with $T$
• Exclusion condition: $Z$ is uncorrelated $ϵ$ because treatment is randomly assigned

1. Then, the first stage (reduced form): $\widehat{T_i}={\gamma }_0+{\gamma }_{1}Z+{\gamma }_2{X}_{2i}+{\nu }_i$
2. Then the second stage:$Y_i={\beta }_0+{\beta }_1\widehat{T_i}+{\beta }_2{X}_{2i}+{ϵ}_i$

Attrition §

def. Attrition means dropping out. The following regression assesses if treatment is correlated to attrition:

$${\text{didAttrition}}_i={\delta }_0+{\delta }_1{\text{isTreated}}_i+{\nu }_i$$

→ if ${\delta }_1$ is statistically significant the attrition is correlated to treatment, thus we need to control for it. Methods to resolve attrition:

1. Add covariates that are significant when we test (interactive attrition test): ${\text{didAttrition}}_i={\delta }_0+{\delta }_1{Z}_i+{\delta }_2{X}_{2i}+{\delta }_3{Z}_i\times X_{2i}$, where $Z$ is the intention-to-treat binary variable.
   • This should also be significant $\widehat{{\gamma }_1}$in the balance test: $X_{2i}={\gamma }_0+{\gamma }_1{Z}_i+{\nu }_i$
   • Add the significant covariates to the final analysis
2. Trim either dataset so the attrition rate is the same
3. Selection model. (not discussed)