Binomial Tree Model of Security Pricing

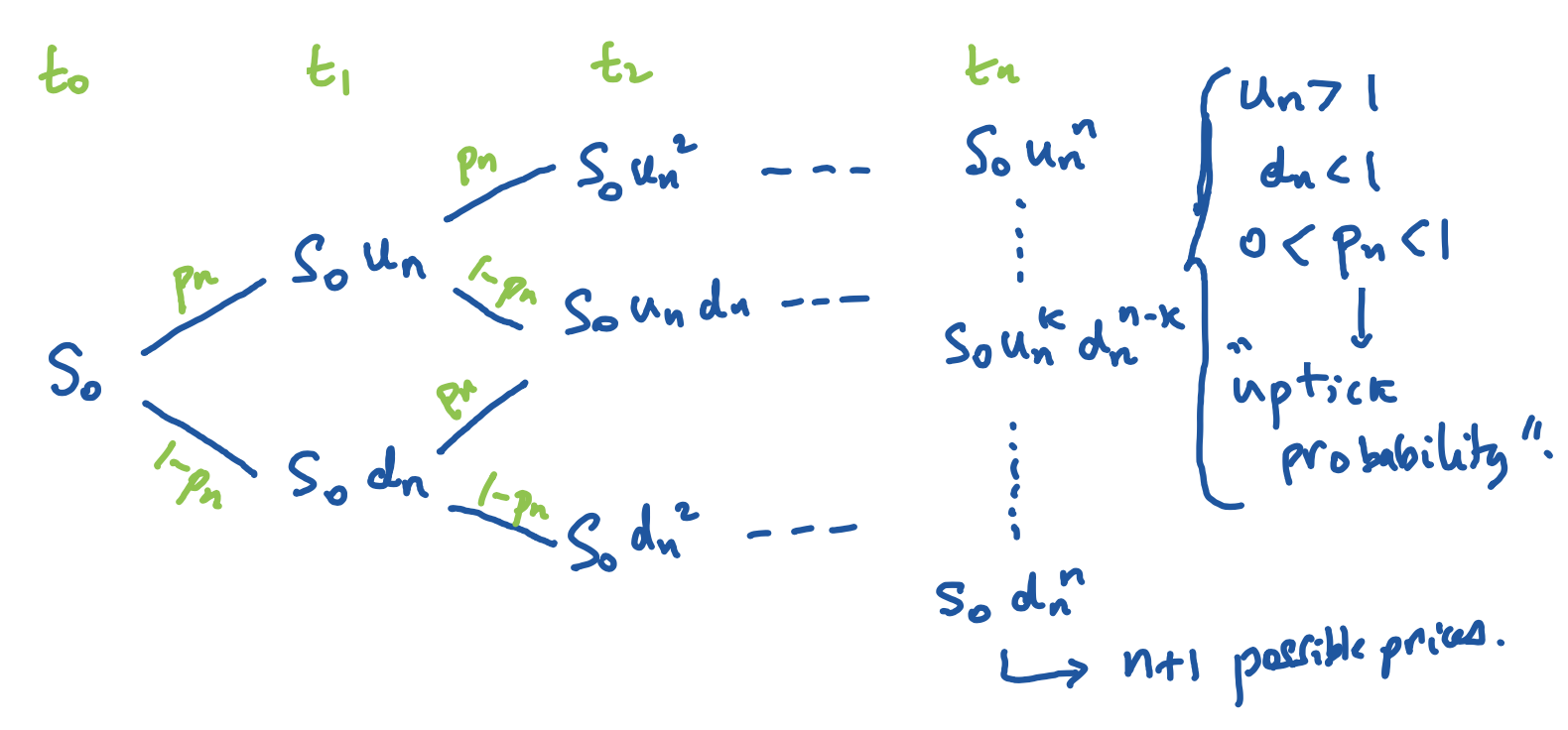
Model Definition §

• Consider time interval $[t_0,t_f]$
  • total time $\tau =t_f-t_0$
  • $n$ intervals
  • $h_n$: duration of one interval ($=\frac{t_f-t_0}{n}$)
• $S_t$: price of security at time $t$.
  • $S_0$ is given as a constant
• Gross return $\frac{S_j}{S_{j-1}}$
  • It’s called gross because its in the form of $1.\text{xx}$ or $0.\text{xx}$, not $\frac{S_j-S_{j-1}}{S_{j-1}}$
  • Is defined as a Bernouilli Distribution:

$$\frac{S_j}{S_{j-1}}=\{\begin{array}{llc}{u}_n& \text{with probability}{p}_n& \text{(stock uptick)}\\ d_n& \text{with probability}(1-p_n)& \text{(stock downtick)}\end{array}$$

• $N$: number of upticks. Is a random variable with Binomial Distribution $N\sim \text{Binom}(n,p_n)$
  • $P(N=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p_n^k(1-p_n{)}^{n-k}$
• Sample Space ${\Omega }_n$
  • $\Omega =\{U,D\}$
  • ${\Omega }_2=\{UU,UD,DU,DD\}$
  • ${\Omega }_3=\{UUU,UUD,\dots ,DDD\}$
  • ${\Omega }_n$ is for $n$-period binomial tree
  • $Pr(\omega ):=p_n^{N(\omega )}(1-p_n{)}^{N(\omega )}$
• Final Price $S_n=S_0{u}_n^k{d}_n^{n-k}$
  • $S_n$ is a random variable. $P(S_n=S_0{u}_n^k{d}_n^{n-k})=P(N=k)$
  • i.e. probability that price will be equal to there being $k$ upticks is the probability that there will be $k$ upticks. (no shit)
• Expectation of final price: $E(S_n)=S_0(p_n{u}_n+(1-p_n)d_n{)}^n$
• To find number of upticks $k$ from final price $S_n$ we use

$$k=\ln \left(\frac{S_n}{S_0{d}^n}\right)/\ln \left(\frac{u}{d}\right)$$

• Dividends: $D(t_{j-1},t_j)=qS(t_{j-1})h_n$
  • See Dividend Discount Model for dividends in non-binomial tree model
  • Total Return (incl. dividends): $R(t_{j-1},t_j)=\frac{S(t_j)-S(t_{j-1})+D(t_{j-1},t_j)}{S(t_j)}={\mathcal{R}}_j+q{h}_n$
  • Capital Gains Return (excl. dividends): ${\mathcal{R}}_i:=\frac{S_1-S_0}{S_0}$
  • (Dividends Return $q{h}_n$)

Assumptions & Definitions §

• Log returns: $Y_{n,j}:=\ln \left(\frac{S_j}{S_{j-1}}\right)$ Is also a random variable
  • Log normal is another indicator of how well the stock is performing
  • It is similar in value to the percentage return
  • See What does the average log-return value of a stock mean? - Personal Finance & Money Stack Exchange for the intuition
• $u_n{d}_n=1$ i.e. the stock ticking up then down is same as no movement at all
• Instantaneous Rate of Return
  • $m={\lim }_{n\to \infty }\frac{E[R(t_0,t_1)]}{h_n}$
• Drift: Instantaneous Expected Log-Return
  • $\mu ={\lim }_{n\to \infty }{Y}_{n,j}={\lim }_{n\to \infty }\frac{E\left[\ln \frac{S_1}{S_0}\right]}{h_n}$
• Log Variance: Instantaneous Variance of Log-Return = Volatility ($\sigma$)
  • ${\sigma }^2={\lim }_{n\to \infty }{\sigma }_n^2={\lim }_{n\to \infty }\frac{Var\left[\ln \frac{S_1}{S_0}\right]}{h_n}$
• Dividend Rate $q$

Lemmas §

• ${\mu }_n{h}_n=p_n\ln u_n+(1-p)\ln d_n$
• ${\sigma }_n^2{h}_n=p_n(1-p_n){\left[\ln \frac{u_n}{d_n}\right]}^2$
• $\mu =m-q-\frac{{\sigma }^2}{2}$
• (Proofs in notes)

thm. Parameter Triple. Given a security with $\mu ,{\sigma }^2,m,q$ we determine that:

1. $u_n\approx e^{\sigma \sqrt{h_n}}$
2. $d_n\approx e^{-\sigma \sqrt{h_n}}$
3. $p_n\approx \frac{1}{2}\left(1+\frac{\mu }{\sigma }\sqrt{h_n}\right)=\frac{e^{(m-q)h_n}-d_n}{u_n-d_n}$

Continuous Time Model §

Model Definition §

Instead of assuming an uptick-downtick gross return is a Bernouilli Distribution, we instead think of the log returns. (Use Lindenberg CLT)

$$\begin{array}{rlr}{S}_n(t)& =S_0\exp \left(\ln \frac{S_n}{S_0}\right)& \\ & =S_0\exp \left(\sum _{j=1}^n\ln \frac{S_j}{S_{j-1}}\right)& \text{Lindenberg CLT}\\ & =S_0\exp \left(Y_{n,j}\right)& Y\sim N(n{\mu }_n{h}_n,n{\sigma }_n^2{h}_n)\\ & =S_0\exp (\mu t+\sigma t\cdot Z)& Z\sim N(0,1)\end{array}$$

⇒ Thus we have

$$\ln \left(\frac{S_t}{S_0}\right)\sim N(\mu t,{\sigma }^{2}t)$$

Properties

• $S(t)$ is a lognormal random variable
  • i.e. $S(t)=S_0{e}^{\mu t+\sigma \sqrt{t}\mathbb{Z}t}$ where $\mathbb{Z}$ is the standard normal random variable
• $\ln \left(\frac{S_t}{S_{t-1}}\right)$ are i.i.d.