Two-Stage Lease Squares Regression

Motivation. Instrumental variables are an advanced way of removing endogenity. Suppose you want to see the effects of police on crime rates. But does crime cause more police to be hired, or does more police cause less crime? Because of this circularity, it’s hard to isolate simply the causality from police to crime rates. So to isolated the exogenous variation in police hiring (i.e. get the pure exogenity), we can use a proxy or instrumental variable: firefighters. Exogenous factors both cause firefighters and police to be hired (policy changes, citizen support) but they don’t cause crime rates to increase.

2-Stage Lease Squares §

Instrumental variables are implemented using 2SLS.

1. We have the first stage (=reduced form), where we regress the independent variable (police) with instrumental variable (firefighters):

$$\underset{\text{ police }}{\underbrace{\widehat{X_{1i}}}}={\gamma }_0+{\gamma }_1\underset{\text{ firefighters }}{\underbrace{Z_i}}+{\gamma }_2\underset{\text{ some control }}{\underbrace{X_{2i}}}+{\nu }_i$$

2. Then we take the ==police estimator ${\hat{X}}_{it}$ (not the actual data!)== and then regress dependent (crime) against estimated independent (estimated police):

$$Y_i={\beta }_0+{\beta }_1\underset{\text{ estimated }}{\underbrace{{\hat{X}}_{1i}}}+{\beta }_2\underset{\text{ control }}{\underbrace{X_{2i}}}+{ϵ}_i$$

Visualization.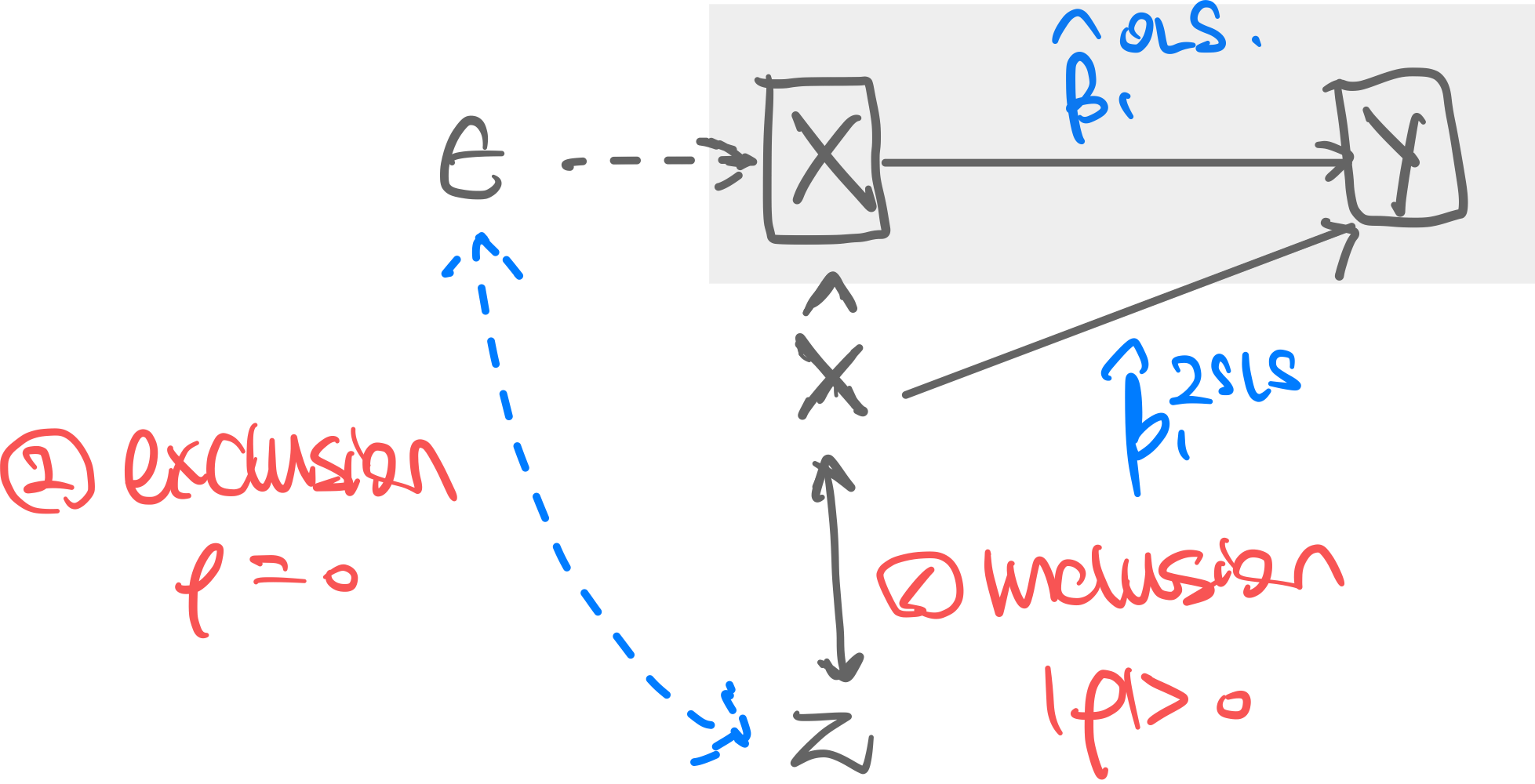

What Are Good Instrumental Variables? §

1. Inclusion condition: $Z$ needs to have meaningful influence on $X$
   1. Satisfied when in the first stage ${\gamma }_1$ is significant at 1%.
2. Exclusion condition: $Z$ needs to have no infludence on $Y$
   • in other words, $Z$ and $ϵ$ should not be correlated.
   • But this cannot be tested directly because $ϵ$ is not observed.
     • → thus the exclusion condition is more of a “it’s probably okay” argument
   1. ! running regression $Y$ against $Z$ might seem prudent but actually if $Z$ is correlated with $\hat{X}$ and $\hat{X}$ with $Y$ then it will always be significant
   2. The best we can do is include more controls we assume are inside $ϵ$ that correlate with $Z$, such that the new $ϵ$ with more controls are not correlated to $Z$.

Multiple Instruments §

Perform the first stage with each instruments $Z_1,Z_2,\dots$:

$$X_{1i}={\gamma }_0+{\gamma }_1{Z}_{1i}+{\gamma }_2{Z}_{2i}+\cdots +{\nu }_i$$

and then same for the second stage.

Over-identification test tests the exclusion restriction. if you’ve gotten the correct multiple instrumental variables. (Overidentification is a good thing.) If we want to see if $Z_1$ and $Z_2$ together satisfy the exclusion condition we test:

1. First stage just with $Z_1$ to get ${\widehat{X_1}}^{Z_1}$. Then the second stage to get ${\widehat{{\beta }_1}}^{Z_1}$
2. First stage just with $Z_2$ to get ${\widehat{X_1}}^{Z_2}$. Then the second stage to get ${\widehat{{\beta }_1}}^{Z_2}$
3. If ${\widehat{{\beta }_1}}^{Z_1}\approx {\widehat{{\beta }_1}}^{Z_2}$ then good!
4. ! but if they’re similar this might just mean that both are bad in similar ways…
5. And If they’re different, there’s no way of knowing which one is the better one Alternatively, run

$$\widehat{{ϵ}_i}=\widehat{{\alpha }_0}+\widehat{{\alpha }_1}{Z}_{1i}+\widehat{{\alpha }_2}{Z}_{2i}+{\alpha }_3{X}_{2i}$$

and then F-test: $H_0:{\alpha }_1={\alpha }_2=0$. A exclusion-condition compatible IV should not be jointly significant. But this is also inaccurate in the same way described above.

Comparison with Ordinary Least Squares §

We should use 2SLS instead of OLS when we know that $X$ is very much endogenous, and we have found a good IV, $Z$ that satisfies the inclusion and exclusion conditions. To test if $X$ is endogenous enough for 2SLS to be useful, we use the following: def. Durbin-Wu-Hausman Test of $X$’s endogenity. Observe first the fact that assuming $Z$ is exogenous:

• if $X$ is exogenous: ${\hat{\beta }}^{\text{OLS}}\approx {\hat{\beta }}^{\text{2SLS}}$
  • i.e. ${\rho }_{X,ϵ}\approx 0$ already, so why use IV or 2SLS?
• if $X$ is endogenous: ${\hat{\beta }}^{\text{OLS}}\ne {\hat{\beta }}^{\text{2SLS}}$
  • i.e. ${\rho }_{X,ϵ}\ne 0$ so we must use IV or 2SLS! The test has null hypothesis $H_0:{\hat{\beta }}^{\text{OLS}}={\hat{\beta }}^{\text{2SLS}}$. If we reject the null, then we should use 2SLS.

Bias in 2SLS §

• def. Quazi-instruments are instruments where there exists some (small) ${\rho }_{Z,ϵ}\ne 0$ (Usually okay, see below)
• def. Weak Instruments are instruments where there exists some ${\rho }_{Z,X_1}\ne 0$. (Usually bad, see below) It’s sometimes okay to have some correlation between $Z$ and $ϵ$, but having correlation between $Z$ and $X_1$ is pretty bad. To see why, observe the 2SLS bias of $\widehat{{\beta }_1}$

$$\underset{n\to \infty }{\lim }{\widehat{{\beta }_1}}^{\text{2SLS}}={\beta }_1+\underset{\text{ bias }}{\underbrace{\frac{{\rho }_{Z,ϵ}}{{\rho }_{Z,X_1}}\frac{{\sigma }_{ϵ}}{{\sigma }_{X_1}}}}$$

Compare this to vanilla OLS (for Consistency ${\rho }_{X,ϵ}=0$):

$$\underset{n\to \infty }{\lim }{\widehat{{\beta }_1}}^{\text{OLS}}={\beta }_1+\underset{\text{ bias }}{\underbrace{{\rho }_{X,ϵ}\frac{{\sigma }_{ϵ}}{{\sigma }_X}}}$$

This implies

• When it has a strong first stage relationship (=${\rho }_{Z,X_1}$ is small) the 2SLS’s ${\widehat{{\beta }_1}}^{\text{2SLS}}isbe\text{er}$
• & If $\frac{{\rho }_{Z,ϵ}}{{\rho }_{Z,X_1}}<1$ then 2SLS has less bias than vanilla OLS even if ${\rho }_{Z,ϵ}\ne 0$
• ! If $\frac{{\rho }_{Z,ϵ}}{{\rho }_{Z,X_1}}>1$ then 2SLS amplified any small correlation ${\rho }_{Z,ϵ}$ and easily becomes worse than vanilla OLS

Rule of Thumb for determining weak instruments

Use 2SLS with instrument $Z$ when in the first stage regression the test

$$\{\begin{array}{ll}>H_1& \text{if }{\gamma }_0={\gamma }_1={\gamma }_2=\cdots \\ H_0& \text{if else}\end{array}>$$

i.e. an F-test, $F>10$.

• Even when ${\rho }_{Z,ϵ}=0$, since the above equations are for ${\lim }_{n\to \infty }$, when $n$ is small bias still exists (in the same direction as OLS).
  • This bias will eventually go away in bigger $n$ (or, of ${\rho }_{Z,ϵ}\ne$, go the opposite way!)

Precision of 2SLS §

Recall multivariate OLS variance of coefficients is:

$$\text{Var}(\widehat{{\beta }_1})=\frac{{\hat{\sigma }}^2}{N\cdot \text{Var}(X_1)\cdot (1-R_1^2)}$$

The 2SLS variance of coefficient is:

$$\text{Var}(\widehat{{\beta }_1})=\frac{{\hat{\sigma }}^2}{N\cdot \text{Var}(\widehat{X_1})\cdot (1-R_{{\widehat{X_1}}^{NoZ}}^2)}$$

The differences are:

• ${\hat{\sigma }}^2$(=second stage regression variance) may be larger because $ϵ$ has been purged
  • This simplies that explainatory power in the observed $X_{1i}$ that were correlated with $ϵ$ is purged (=thus total reduced)
• $\text{Var}(\widehat{X_1})$, not $\text{Var}(X_1)$ because we use estimates (see above) not actual data during regression
  • $\text{Var}(\widehat{X_1})$ is probably smaller because we purged $ϵ$-related variance.
• ! $R_{{\widehat{X_1}}^{NoZ}}^2$ is the R-squared from the new regression

$$\widehat{X_{1,i}}={\pi }_0+{\pi }_1{X}_{2i}+{\eta }_i$$

- This regression determines how much does $X_{2}$, not $Z$, determines $\hat{X_{1}}$.
- $R^{2}$ in this regression thus measures the collinearity of $\hat{X_{1}}$ and $X_{2}$ (=controls)
    - btw, $R^{2}$ in the second regression doesn't mean shit.
- The lower the explanatory power of $Z$ on $\hat{X_{1}}$, the higher this value is, and the higher the variance of the 2SLS coefficient is.