Logistic Model

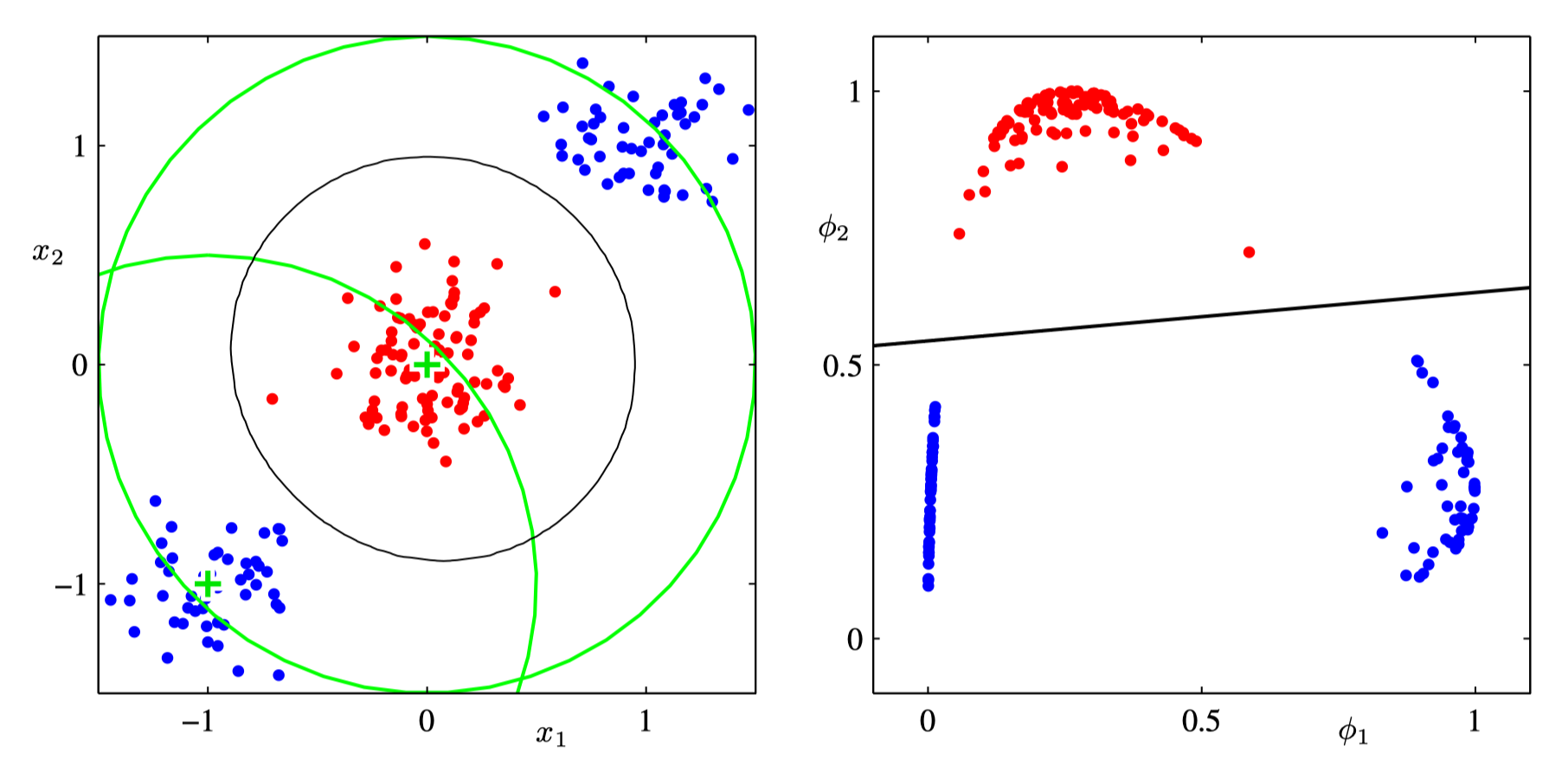
Motivation. Suppose there was a transformation from the input space into a “feature space”, where all datapoints where nicely linearly dividable, like the following: Then, let’s run a classifier using a logistic model (=Softmax and Sigmoid) We will:

1. Construct a likelihood of a single datapoint being classified correctly
2. Construct a likelihood of all datapoints classified correctly
3. Use the negative of log-likelihood as a error function to minimize
4. Calculate the gradient of that error function The input data is mapped into a output classification like this:

$${\mathbb{R}}_{\text{input space}}^D\stackrel{\varphi }{⟼}{\mathbb{R}}_{\text{feature space}}^F\stackrel{w_1,\dots ,w_k}{⟼}\underset{\text{ ’activations’ }}{\underbrace{a_1\dots a_K}}\stackrel{\text{softmax}}{⟼}p(C_1|\varphi )=:y_1\dots y_K$$

• $D$ is the dimension of the input space
• $F$ the feature space (how many features there are).
• $K$ is the number of classes.
  • Note that the output $\vec{y}=(y_1,\dots ,y_K)$ is a one-hot encoding.
  • We have a weight vector ${\mathbf{w}}_k$ for each feature $k$.
• We are given $N$ datapoints $\{({\mathbf{x}}_n,{\mathbf{t}}_{\mathbf{n}})\}$
  • ${\mathbf{t}}_{\mathbf{n}}$ is in this case also a vector because the target is one-hot encoded as well Visualization. The following visualization of matrix-vector multiplication may clarify this process:

Constructing the Likelihood Function §

We start with $p(C_{k_{\text{class}}}|{\varphi }_{n_{\text{data}}}({\mathbf{x}}_{{\mathbf{n}}_{\text{data}}}))$ which is the density given one data point, $n_{\text{data}}$ for a single class, $k_{\text{class}}$. We omit the ${\mathbf{x}}_{{\mathbf{n}}_{\text{data}}}$ for clarity. Let’s omnit subscript labels too. Then consider the density that a single data point, $n$ has the correct classification (one-hot encoding):

$$p(t_{n_{\text{data}}}|{\varphi }_{n_{\text{data}}};{\mathbf{w}}_1,\dots ,{\mathbf{w}}_K)=\prod _{\forall k\in [K]}p(C_k|{\varphi }_n{)}^{t_{n,k}}$$

Raising to the power simply has the effect of only obtaining $p(\cdot )$ for the class where $t=1$. The rest of the elements of the vector are ignored. And finally that all datapoints have the correct classification:

$$p(\mathbf{T}|{\varphi }_n;{\mathbf{w}}_1\dots {\mathbf{w}}_K)=\prod _{\forall n\in [N]}\prod _{\forall n\in [K]}p(C_k|{\varphi }_n{)}^{t_{n,k}}$$

Error Function §

The error function is the negative-log of the likelihood. Simply:

$$\begin{array}{rl}E({\mathbf{w}}_1,\dots ,{\mathbf{w}}_K)& =-\ln \prod _{\forall n\in [N]}\prod _{\forall k\in [K]}{\underset{\text{ =:yn,k }}{\underbrace{p(C_k|{\varphi }_n)}}}^{t_{n,k}}\\ & =-\sum _{\forall n\in [N]}\sum _{\forall k\in [K]}{t}_{n,k}\ln y_{n,k}\end{array}$$

Coincidentally this error function is the cross-entropy between “distributions” $t_{n,k}$ and $y_{n,k}$. This is just a coincidence and abuse of notation to call it cross-entropy. Moving on; now, consider optimizing for a single weight class, ${\mathbf{w}}_j$. We have:

$$\frac{dE}{d{\mathbf{w}}_j}=-\sum _{\forall n\in [N]}\sum _{\forall k\in [K]}\frac{t_{n,k}}{y_{n,k}}\cdot \frac{d{y}_{n,k}}{d{\mathbf{w}}_{\mathbf{j}}}$$

requires the chain rule. Observing the mapping from the input data to the output probabilities, let’s consider the gradient for just one of the weights, ${\mathbf{w}}_k$ for class $k\in [K]$

$$\frac{dE}{d{\mathbf{w}}_k}=\frac{dE}{d{y}_k}\cdot \frac{d{y}_k}{d\mathbf{a}}\cdot \frac{d\mathbf{a}}{d{\mathbf{w}}_{\mathbf{k}}}$$

We calculate all three of these:

-1.

$$\begin{array}{rl}\frac{dE}{d{y}_k}& =\end{array}$$