Stable Marriage Problem

def. Stable Marriage Problem. Given equal number of heterosexual men and women, where each person has ranked all members of the opposite sex in order of preference, how can we marry the men and women together such that there are no non-married pair $(m,w)$ who would both marry each other than their current partners (=in a unstable marriage)?

Examples.

• Resident—hospital matching
• high school—student matching

def. Gale–Shapely Stable Matching Algorithm (GSSMA) (=propose-accept algorithm)

• Every day…
  • Each man who isn’t engaged proposes to their top women that didn’t reject them before
  • Every women who gets proposed to by $m_1,m_2,\dots$
    • …if they’re already engaged to some $m_0$: accept $\text{max}[m_0,\dots ]$, reject everybody else.
    • …if they’re not engaged to some $m_0$: accept $\text{max}[m_1,\dots ]$, reject everybody else
• Repeat until completes

thm. (GS always terminates at full matching) Lemma. If woman $w$ rejects man $m$, in all future scenarios $w$ is engaged to $m^{\prime }$ who she likes better than $m$. Proof by Contradiction. Suppose there is a man $m$ who is not matched; i.e. $m$ is rejected by everybody.

• By the lemma, all women are engaged to somebody better than $m$.
• But if all women are engaged, and there are equal number of men and women, $m$ cannot exist. ■

thm. (GS matching is stable) Proof by contradiction. Assume there exists an unstable match $(m_1,w_2),(m_2,w_1)$, but $w_1{\succ }_{m_1}{w}_2$ and $m_1{\succ }_{w_1}{m}_2$:

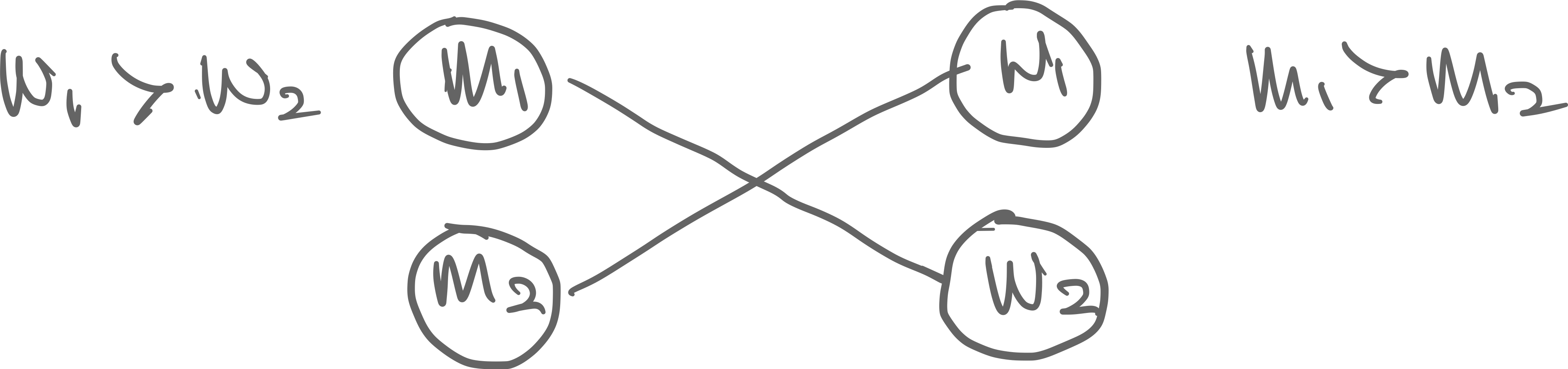
• $m_1$ must have proposed to $w_1$ and been rejected before proposing to $w_2$ by the structure of the algorithm
• By lemma above, $w_1$’s final fiancé, $m_2$, must have been preferable to $m_1$. But this is not true. This is a contradiction.■

def. Valid Partner. $w$ is a valid partner of $m$ if there exists any stable matching where $(m,w)$ is a match (doesn’t have to be found by GS).

thm. (Proposer wins in GS). GS where men propose, men get the best valid partner possible. In other words all men $m$ with their set of valid partners $S_m\subseteq \text{Women}$, never get rejected by any women in $S_m$. Proof by Contradiction. Assume there exists a valid rejection of a man’s proposal by a woman. Consider the first timepoint when a man $m$ gets rejected by a valid partner $w$.

• $w$ must have rejected $m$ because she is already engaged with $m^{\prime }$ who she prefers more. (‡)
• $w$ is engaged to man $m^{\prime }$. $m^{\prime }$’s most preferred partner in $S_m$ is $w$ by definition of this timepoint (†) Now, consider a completely different stable match (not by GS). There must exist a stable matching where $(m,w)$ is a match because $w$ is a valid partner of $m$. In this matching, let $w^{\prime }$ be $m^{\prime }$’s match. Now, $w^{\prime }$ is not the most preferred valid partner $S_{m^{\prime }}$ because $m^{\prime }$ prefers $w$ the most, as we saw in (†). $w$ also is unsatisfied with $m$ because she prefers $m^{\prime }$ more (‡). Therefore this is not a stable matching; this is a contradiction. ■

Remark. Extensions of this stable matching problem is done in CS535 HW5.