Property Exchange

Motivation. Imagine a situation where $n$ people each have their own house. They would like to exchange houses to be better off. How do we go about doing that? In this setting we say:

• Preferences are strict (no agent is indifferent about two different items)

def. Stable allocation (=“in the core”). An allocation $a$ is stable there is no blocking coalition. A blocking coalition for allocation $a$ is a subset of agents who, when trading amongest themselves, achieves a higher utility for at least one agent, and doesn’t reduce the utility of anybody else in the subset.

def. Top Trading Cycles (TTC) algorithm.

1. Algorithm is in multiple rounds
2. Round $k$:
   1. Agents point to favorite remaining house
   2. This graph will always have a cycle, because all edges have out-degree 1 (thm)
   3. Take an arbitrary cycle, and swap houses according to that cycle
   4. Eliminate these people from the graph
3. Repeat

thm. (TTC is strategy-proof w.r.t. individual agents). let allocation $A$ be an allocation generated by TTC. Fixing all other agent’s preferences, no one agent can benefit by lying about their preference ordering. Proof sketch by induction

1. Round 1: Agents point to favorite house.
   1. Let those who win in round 1 be $W_1$; they don’t lie, because they will win their favorite house if they’re truthful.
   2. Those who lose, will proceed to the next round…
2. Round 2: Agents not in $W_1$ (=losers) have not gotten their favorite house; let’s say a loser $\ell \in W_2$ (a round 2 winner) got their $k$-th favorite house as a result of the second round.
   1. Say $\ell$ prefers a house from someone in $W_1$. $\ell$ will lie and point to that house to attempt to be included in the cycle.
   2. However, nobody in $W_1$ pointed to our loser. Therefore the loser will not be able to form a cycle, as long as everybody else is truthful.
3. Induction until final round (assume round $\mathrm{1..}k$ is truthful, then round $k+1$ is truthful. ■

thm. (TTC is stable). Allocation $A$ generated by TTC has no blocking coalition. Proof by contradiction. Suppose there was a blocking coalition they are the black dots. We list them by the rounds in which they won in TTC: $W_1,W_2,\dots$

1. If there is a blocking coalition of agents separated in two disparate rounds of TTC $i,j$ such that $W_i,W_j,i<j$, then the coalition’s alternative trading cycle must have an agent who, in the informal trade, pointed from round $i$ to round $j$. This doesn’t make sense, because they chose their favorite in round $i$ already and won. Thus such a coalition cannot exist.
   1. It is trivial to see also that a coalition spread across three or more rounds of TTC is impossible.
2. If there is a blocking coalition of agents who are all in $W_k$, the TTC algorithm already trades amongst them. Thus such a coalition cannot exist. ■ thm. (TTC is the only stable algorithm) let $A$ be allocation by the TTC algorithm. There exists no other allocation $A^{\prime }$ that is stable. (=TTC is the only allocation in the core.) Proof by Induction and Contradiction. Suppose TTC produced allocation $A$. Presume there was an alternative allocation $A^{\prime }$ that was also stable. Let the agents whose allocation differs between $A$ and $A^{\prime }$ be $S$, the “switchers”.
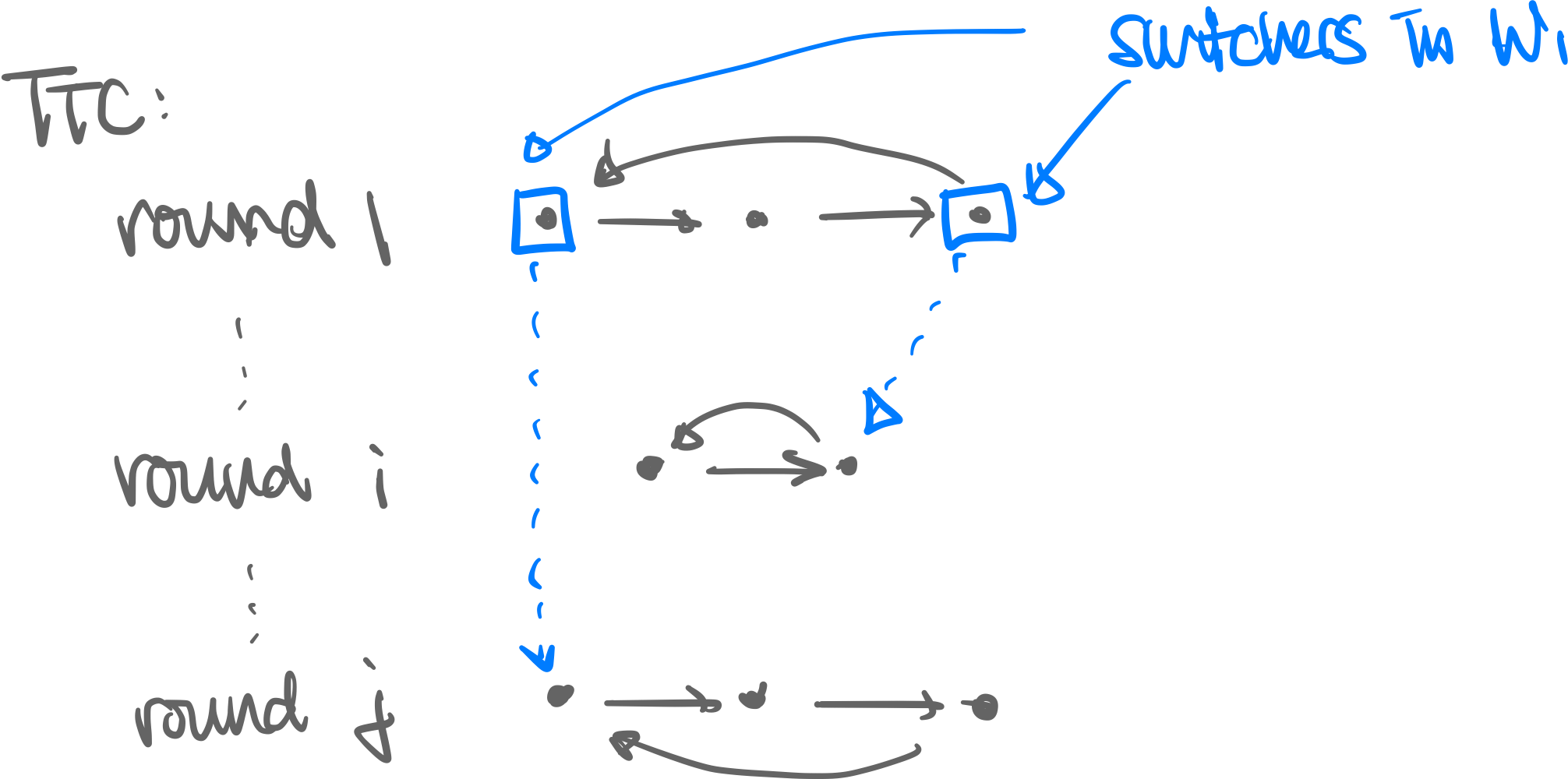
3. Round 1: Let the switchers in $W_1$ be $S_1\subseteq W_1$. Every switcher $s\in S_1$ would gotten switched to an alternative house in a latter round. But since in the TTC $s$ pointed to another agent in $W_1$, this is a contradiction. Therefore, no switcher exists in $S_1$.
4. Round 2: Let the switchers in $W_2$ be $S_2$. Switcher $s\in S_2$ cannot have switched with anybody in $W_1$ because there are no switchers in $W_1$. (equivalent)
5. Induction until final round (assume there are no switchers until round $i$, then any switcher in round $i+1$ must have switched with latter round, but impossible.) ■

Kidney Exchange §

Motivation. Let’s think of an alternative situation. A patient needs a kidney, and the patient’s family or friend wants to donate the kidney to them. However the donor’s may not be compatible with the patient. Therefore we need to find other compatible donor(-patient pair) to do a cross-kidney swap. When there are lots of patient-donor pairs, we need to find a trading cycle with compatible donors. We model the situation such that each patient-donor entity has a compatibility list for all other patient-donor pairs. Think of each patient-donor as one entity. However, Unlike the swapping housing example above we cannot trade along long cycles because we need to operate on all patients simultaneously which is not feasible. Therefore, we only consider a matching; i.e. a pairs of patient-donors do a cross-kidney swap. This is equvalent an (unpartitioned) maximum graph matching problem. Construct an undirected graph:

1. All entities point to any subset of compatible entities (obviously not themselves)
2. If both entities point to each other, then create an undirected edge. Remove all other directed edges. def Priority Matching. On an undirected graph $G$:
3. Randomly fix an ordering of agents.
4. let $M_0:=$ set of all possible maximum matchings on $G$.
   1. Obviously, these maximum matchings are of the same degree (=have same number of edge matchings in them)
5. For $i=1\dots n$ for every entity:
   1. $Z_i$ ← subset of $M_{i-1}$ that includes agent $i$ in the matching
   2. If $Z_i=\varnothing$ then $M_i$← $M_{i-1}$ (if $i$ cannot be included ever, then ignore $i$)
   3. If $Z_i\ne \varnothing$ then $M_i$ ← $Z_i$ (make sure $i$ is included in all subsequent matchings)
6. This will result in $M_n$. Every matching $m\in M_n$ is a matching.

thm. (PM matchings always match same agents.) All matchings $M_n$ returned by PM matches the same agents. Proof Sketch. Inside the loop:

1. If $Z_i=\varnothing$ then agent $i$ is not included in any $m$.
2. If $Z_i\ne \varnothing$ then agent $i$ is definitely included in all $m$.

thm. (PM is DSIC) In PM, all agents will always report all of their compatible partners. Proof Sketch. Reporting a lesser number of edges will only reduce the edges they are connected to, and thus only makes it less possible to be included in a matching.