Derivative Rules

Note

• (DevonThink) IB Math HL Formula Booklet
• Integration Rules

Derivation Rules §

Chain Rule:

$$y=g(u)⟹u=f(g(x))⟹\frac{dy}{dx}=\frac{dy}{du}\cdot \frac{du}{dx}$$ $$f(g(x))=f^{\prime }(g(x))\cdot g^{\prime }(x)$$

Product Rule:

$$\frac{d}{dx}f(x)g(x)=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$$

Filliping:

$$\frac{dy}{dx}=(\frac{dx}{dy}{)}^{-1}$$

Special Functions §

Exponentials §

• $f(x)=a^x$ then $f^{\prime }(x)=\ln (a)\cdot a^x$
• $f(x)=e^x$ then $f^{\prime }(x)=e^x$
• $f(x)=a^{g(x)}$ then $f^{\prime }(x)=\ln (a)\cdot a^{g(x)}\cdot g^{\prime }(x)$
• $f(x)=e^{g(x)}$ then $f^{\prime }(x)=e^{g(x)}\cdot g^{\prime }(x)$

Trigonometric Functions §

From (DevonThink) Mnemonic diagram for trigonometric and hyperbolic functions

1. Functions and cofunctions are on horizontal lines.
2. Derivatives of functions on the right have a negative sign; those on the left do not.
3. Functions and reciprocals are on diagonal lines.
   1. e.g. $\sin (x)=\frac{1}{\csc (x)}$
4. Each function is the ratio of the next two functions clockwise.
   1. e.g. $\tan (x)=\frac{\sin (x)}{\cos (x)}$
5. Each function the the product of its two neighbors.
6. The two functions at the top are bounded. The rest are unbounded.
7. The functions that are vertices of a triangle with a Roman numeral inside are related by Pythagorean identities.
   1. e.g. $\sin (x{)}^2+\cos (x{)}^2=1$

Function	Derivative	Integral
$\sin (x)$	$\cos (x)$	$-\cos (x)+C$
$\cos (x)$	$-\sin (x)$	$\sin (x)+C$
$\tan (x)$	${\sec }^2(x)$	$-\ln
$\cot (x)$	$-{\csc }^2(x)$	$\ln
$\sec (x)$	$\sec (x)\tan (x)$	$\ln
$\csc (x)$	$-\csc (x)\cot (x)$	$\ln

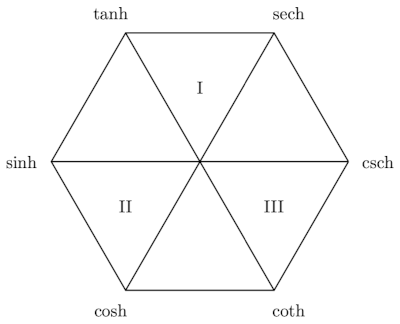
1. Function and cofunctions are on lines that make a 120° angle with the horizontal.
2. Derivatives of functions on the right have a negative sign; those on the left do not.
3. Functions and reciprocals are on diagonal lines.
4. Each function is the ratio of the next two functions clockwise.
5. Each function the the product of its two neighbors.
6. The two functions at the top are bounded. The rest are unbounded.
7. The functions that are vertices of a triangle with a Roman numeral inside are related by Pythagorean identities.