Context-Free Grammar

Section: Pushdown Automata

def. a Context-Free Grammar (CFG) is a grammar whose production rules consist of:

$$A\to \mathbf{x}$$

…where $A$ is a variable, and $\mathbf{x}$ is a string of variables and terminals.

CFGs can check for syntactically correct programs

• Simple Grammar: a CFG where any pair of $(var,term)$ appear in no more than one rule.
• Ambiguous Grammar: there exists a string in the language that has more than one derivation.

def. a Parse Tree [=Derivation Tree] shows the derivation steps of a single string from a start symbol according to the rules of a grammar.

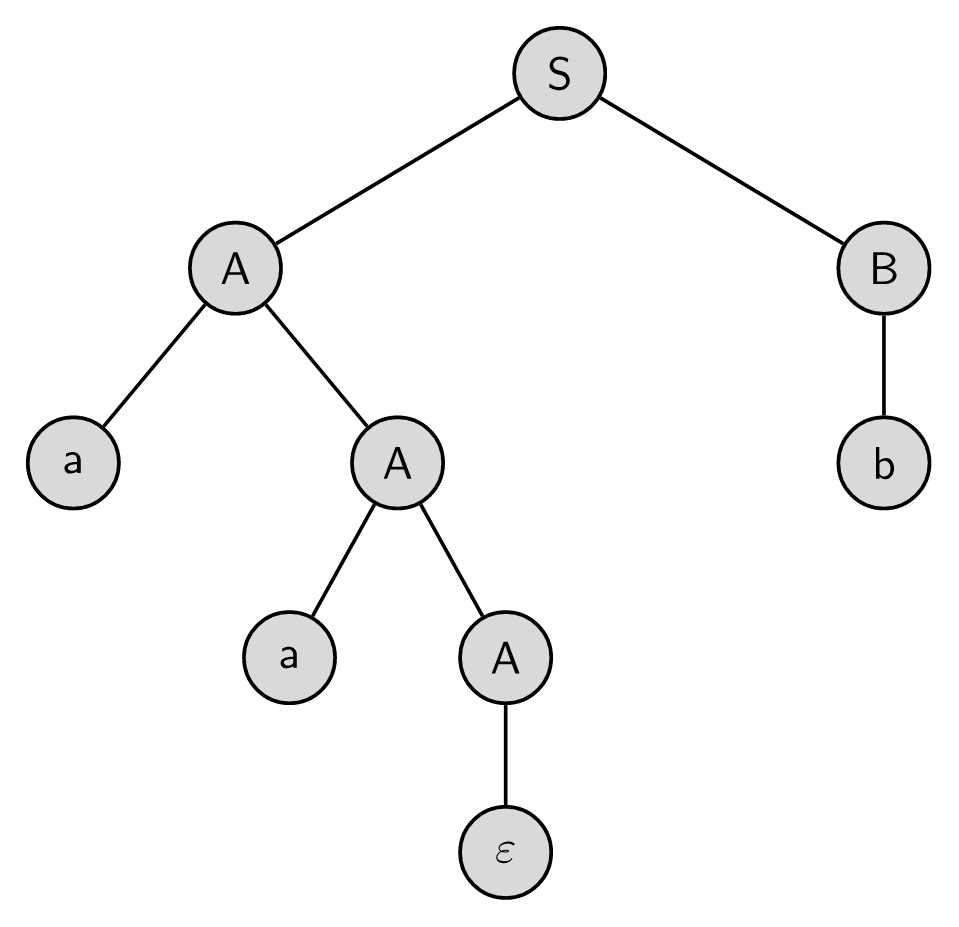
• The leaves of the tree read right-to-left is the yield of the tree—in this case, $aaϵb$ is the yield.
• The yield should not contain the $\lambda$s. (obviously)

def. Leftmost Derivation. Replace the leftmost variable in every step.

def. Rightmost Derivation. Replace the rightmost variable in every step.

Normal Forms §

def. Chomsky Normal Form. A CFG is in CNF iff all rules are in the form:

$$\begin{array}{rlr}A& \to BC& \text{two vars}\\ A& \to a& \text{one terminal}\end{array}$$

• thm. All CFGs can be expressed in CNF¹ def. Greibach Normal Form. A CFG is in GNF iff all rules are in the form:

$$A\to \underset{\text{ terminal }}{\underbrace{a}}\underset{\text{ only vars }}{\underbrace{BCD\dots }}$$

---

thm. Determinability. If the CFG doesn’t contain rules of the form $A\to \lambda$ or $A\to B$, then we can determine for all $w$ if it is in the language of the CFG.

thm. a Context-Free Grammar is equivalent to an NPDA.

NPDA → CFG §

alg. Given NPDA, you can define an equivalent CFG in the following steps:

1. For any transitions that pop/push more than one variable onto the stack:
   1. Use a new state to split out the transition, so that one transition only push/pops one variable onto the stack
2. Then, for each transition arc:
   1. If the transition arc is a pop arc that pops $A$ off the stack, i.e.: from state $i$ to $j$ is in the form $t,A;\lambda$, then construct a production rule for the grammar as: $(q_i,A,q_j)\to t$
   2. If the transition arc is a push arc that pushes $A$ onto the stack i.e.: from state $i$ to $j$ is in the form $t,\gamma ,A\gamma$ then construct a production rule for the grammar as: $(q_i,\gamma ,q_k)\to t(q_{j}A{q}_l)(q_l\gamma q_k)$, where $q_k,q_l$ is every possible combination of states in the PDA(!)
3. Finally, of all the rules generated, if any variables on the right side of the arc don’t appear on the left side, that rule is useless.

CFG → NPDA §

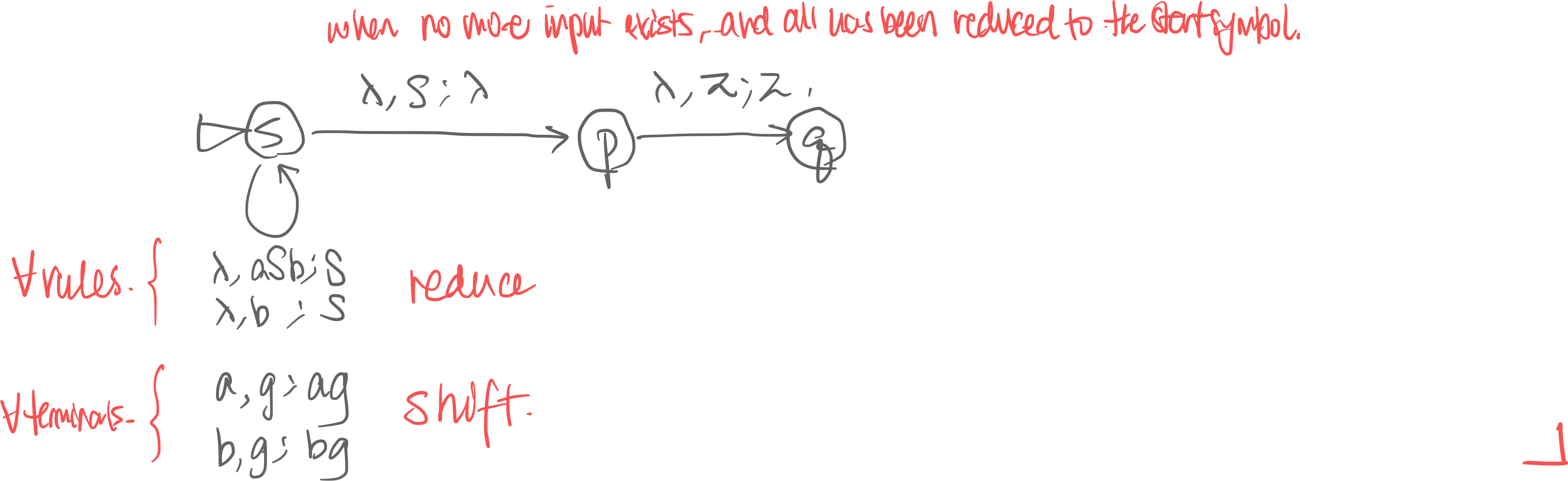
alg. Given a CFG, you can build an LL-NPDA in the following steps. This is a top-down design:

1. There are 3 total states in the NPDA: 0, 1, 2
2. Move from state 0 to state 1 by adding the start variable S onto the stack
3. The middle state has loops for every rule of the CFG. Pop off the LHS, add the RHS to stack while processing any beginning terminals
4. Move from state 1 to final state 2 in a $\lambda$-transition

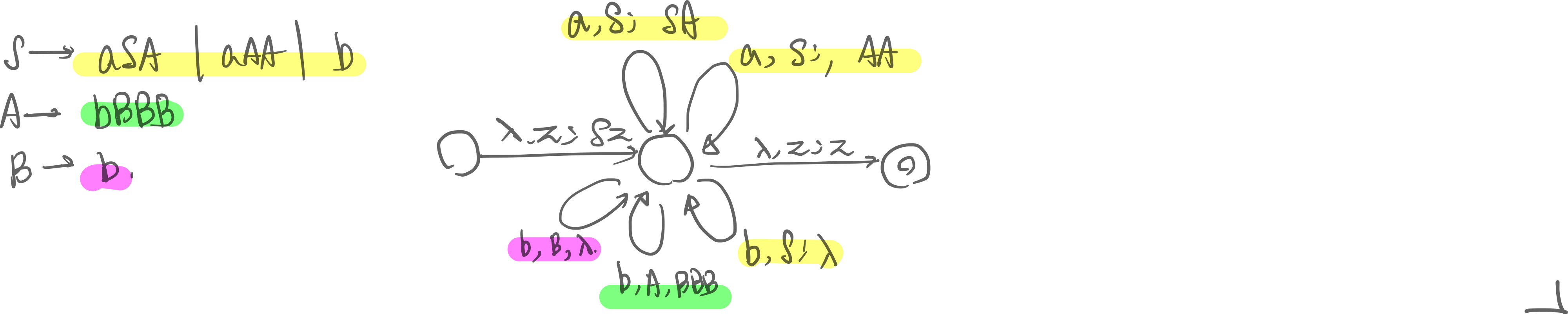
alg. Given CFG, you can build an LR-NPDA in the following steps. This is a bottom-up design:

1. There are 3 total states in the NPDA: 0, 1, 2
2. State 0 has loops for:
   1. …every rule of the grammar. Each rule will pop the RHS and push the LHS of the rule
   2. …every terminal of the grammar. Each terminal will be pushed onto the stack while reading that terminal.

---

Context-Free Language Parsing

Footnotes §

1. Linz ↩