Central Limit Theorem

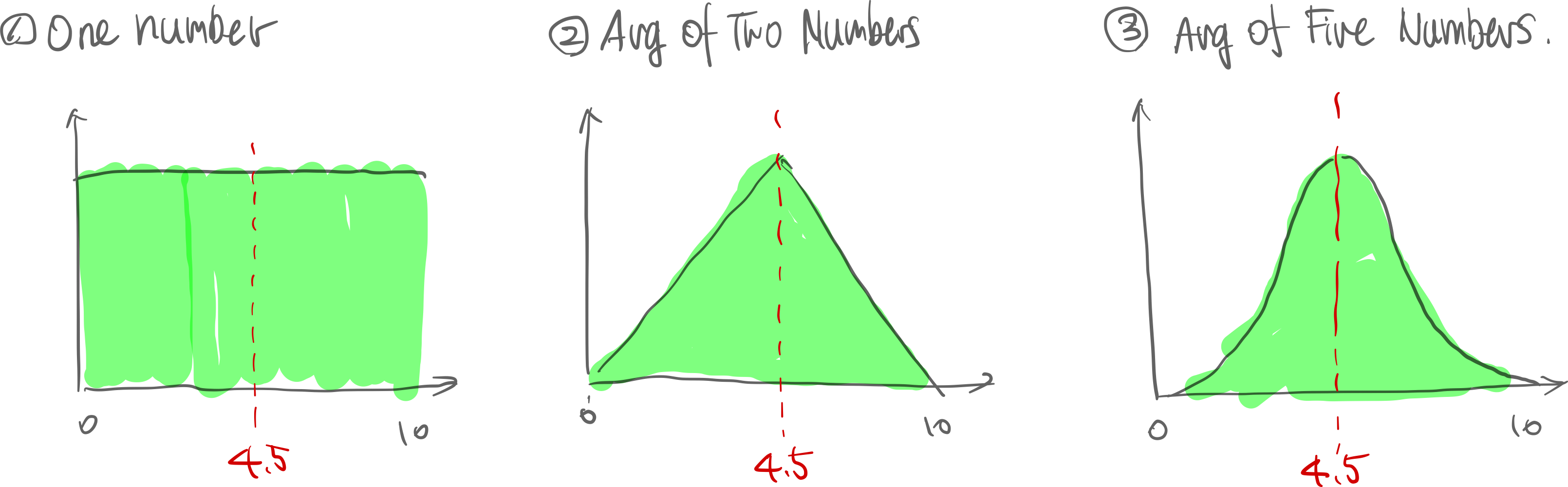
Intuition: Selecting from a box of 1 to 10,

As the sample size ($n$) increases, observe the following:

1. $\mu$ is constant
2. $\text{Var}$ is increasing
3. The distribution apporoaches a bell curve

thm. Law of Averages (=Law of Large Numbers) let $X_1,\dots ,X_n$ be random variables that are i.i.d. If $E(X)=\mu$, and ${\bar{X}}_n=\frac{X_1+\cdots +X_n}{n}$ then for any small value of $ϵ$:

$$\underset{n\to \infty }{\lim }[\mathbb{P}(|X-\mu |<ϵ)]=1$$

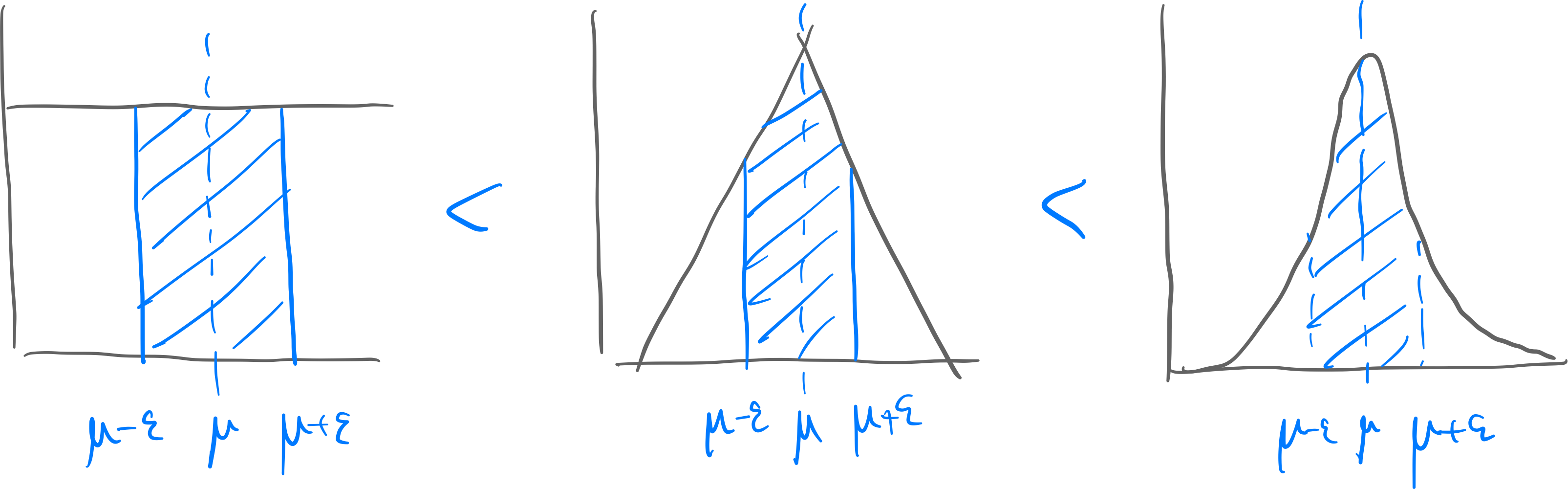
thm. Central Limit Theorem (for averages) let $X_1,\dots ,X_n$ be random variables that are i.i.d. If $E(X)=\mu$, $\text{SD}(X)=\sigma$ and ${\bar{X}}_n=\frac{\sum X_i}{n}$ then for a big value of $n$:

$${\bar{X}}_n\sim \text{Normal}(\mu ,\frac{{\sigma }^2}{n})$$

∵ for ${\bar{X}}_n$ where $n$ is just a constant

• Mean: $\mathbb{E}({\bar{X}}_n)=\mathbb{E}(\frac{X_1+\cdots +X_n}{n})=\frac{1}{n}\cdot n\cdot \mathbb{E}(X_i)=\mu$
• Variance: $\text{Var}({\bar{X}}_n)=\text{Var}(\frac{X_1+\cdots +X_n}{n})=\frac{1}{n^2}\cdot n\cdot \text{Var}(X_i)=\frac{{\sigma }^2}{n}$
• Std. Dev: $\text{SD}({\bar{X}}_n)=\sqrt{\text{Var}({\bar{X}}_n)}=\frac{\sigma }{\sqrt{n}}$

thm. Central Limit Theorem (for sums) let $X_1,\dots ,X_n$ be random variables that are i.i.d. If $E(X)=\mu$, $\text{SD}(X)=\sigma$ and $S_n=X_1+\cdots +X_n$ then for a big $n$:

$${\bar{S}}_n\sim \text{Normal}(n\mu ,n{\sigma }^2)$$

∵ for $S_n$ where $n$ is just a constant

• Mean: $\mathbb{E}(S_n)=\mathbb{E}(X_1+\cdots +X_n)=n\cdot \mathbb{E}(X_i)=n\mu$
• Variance: $\text{Var}(S_n)=\text{Var}(X_1+\cdots +X_n)=n\cdot \text{Var}(X_i)=n{\sigma }^2$
• Std. Dev: $\text{SD}(S_n)=\sqrt{\text{Var}(S_n)}=\sqrt{n}\cdot \sigma$

Abstract

To Summarize, for a big enough value of $n$, and ${\bar{X}}_n$ the average and $S_n$ the sum:

$$\begin{gathered} \mathbb{P}(a<{\bar{X}}_n<b)\simeq {\int }_a^b\text{Normal}[\mu ,\frac{\sigma }{n^2}]={\int }_{\frac{a-\mu }{\sigma /\sqrt{n}}}^{\frac{a-\mu }{\sigma /\sqrt{n}}}\text{Normal[0,1]}=\Phi (\frac{b-\mu }{\sigma /\sqrt{n}})-\Phi (\frac{a-\mu }{\sigma /\sqrt{n}}) \\ \mathbb{P}(a<S_n<b)\simeq {\int }_a^b\text{Normal}[n\mu ,n{\sigma }^2]={\int }_{\frac{a-n\mu }{\sqrt{n}\sigma }}^{\frac{b-n\mu }{\sqrt{n}\sigma }}\text{Normal[0,1]}=\Phi (\frac{b-n\mu }{\sqrt{n}\sigma })-\Phi (\frac{a-n\mu }{\sqrt{n}\sigma }) \end{gathered}$$

rmk. Binomal Approximtion using Normal Distribution. let the following:

• $X\sim \text{Binom}[n,p]$
• Indicator functions s.t. $X=I_1+\cdots +I_n$ where $I_i$ defines the $i$-th event is successful. Note that $I_1,\dots ,I_n$ are all i.i.d. then…
• $\mathbb{E}(I_i)=p$
• $\text{Var}(I_i)=\mathbb{E}(I_i^2)-[\mathbb{E}(I_i){]}^2=\mathbb{E}(I_i)-p^2=p-p^2$ ($\because \forall I=\text{Indicator, }\mathbb{E}(I^2)=\mathbb{E}(\mathbb{I})$)
• For a large enough $n$, $X\sim \text{Normal}[np,np(1-p)]$ ($\because I_1,\dots ,I_n$ are i.i.d., see the additional rule for expectated value and variance)

Lindenberg CLT §

thm. Lindenberg Central Limit Theorem. Given random variables $X_1\dots X_n$, with each $E(X_k)={\mu }_k$, $Var(X_k)={\sigma }_k^2$and the following conditions:

1. They are independent (No need to be identically distributed)
2. ${\lim }_{n\to \infty }\frac{1}{\sum {\sigma }_k^2}E((X_k-{\mu }_k{)}^2{1}_{|X_k-{\mu }_k>ϵ\sum {\sigma }_k^2})$ i.e. variance is not too big ⇒ Then

$$\frac{{\sum }_{k=1}^n(X_k-{\mu }_k)}{\sqrt{{\sum }_{k=1}^n{\sigma }_k^2}}{⟶}_{n\to \infty }^{d}N(0,1)$$