Epic and Mono

Motivation. Consider the definitions of a surjective and injective function. In category theory we don’t want to have a definition based on specific property of objects. So we try to define a surjective and injective morphism only based on objects, morphisms and their composition.

In category $\mathcal{C}$:

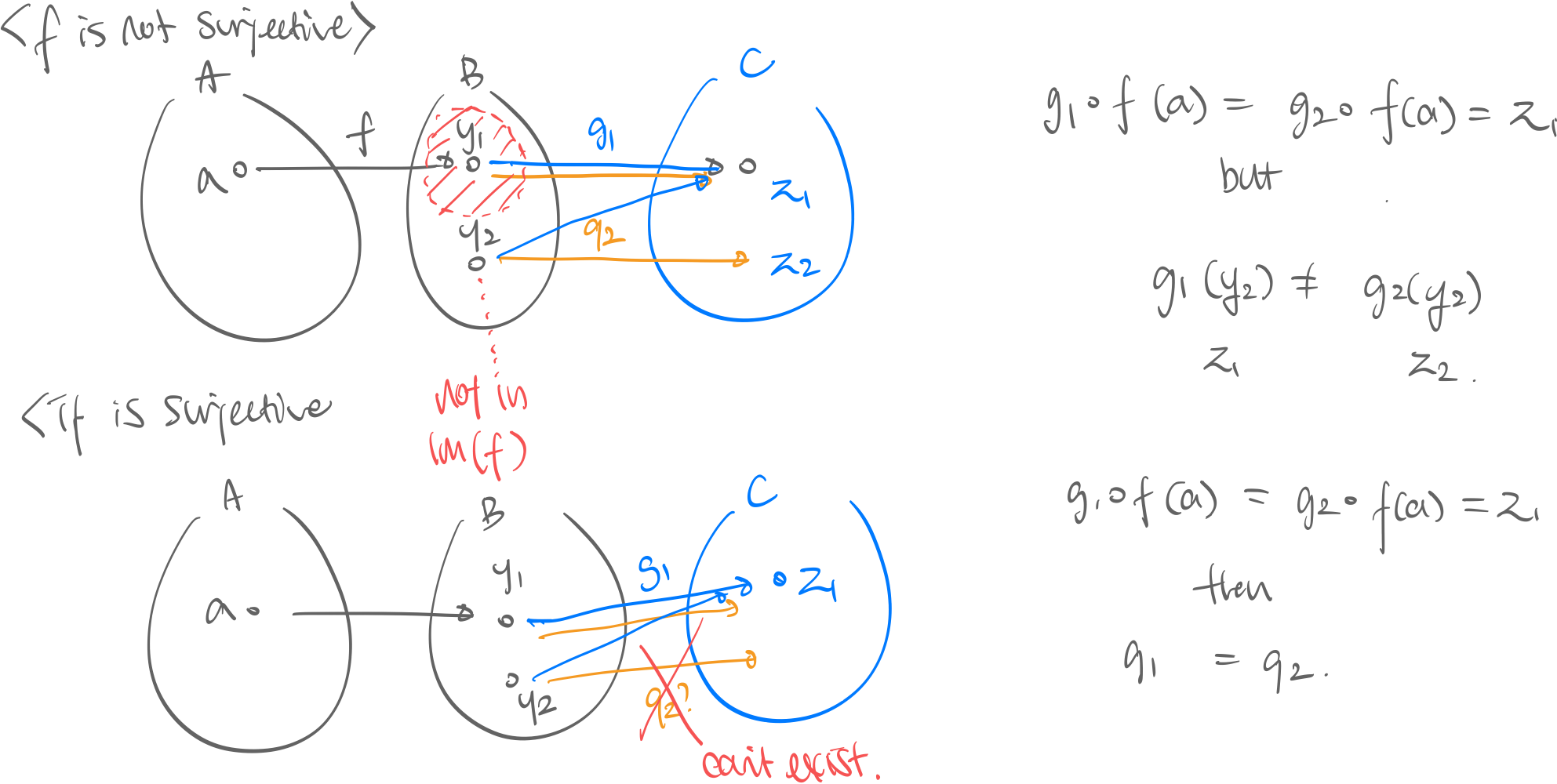
def. Epimorphism (=Epic morphism). Consider $f::A\to B$.

1. let $g_1,g_2::B\to C$
2. $\forall C\in \text{Obj}(C).\forall g_1.g_2.,$ if $g_1\circ f=g_2\circ f$ implies $g_1=g_2$…
3. …then $f$ is an epimorphism.

def. Monomorphism (Mono morphism). Consider $f::A\to B$.

1. let $g_1,g_2::C\to A$
2. $\forall C\in \text{Obj}(C).\forall g_1.g_2.$, if $f\circ g_1=f\circ g_2$ implies $g_1=g_2$…
3. …then $f$ is a monomorphism

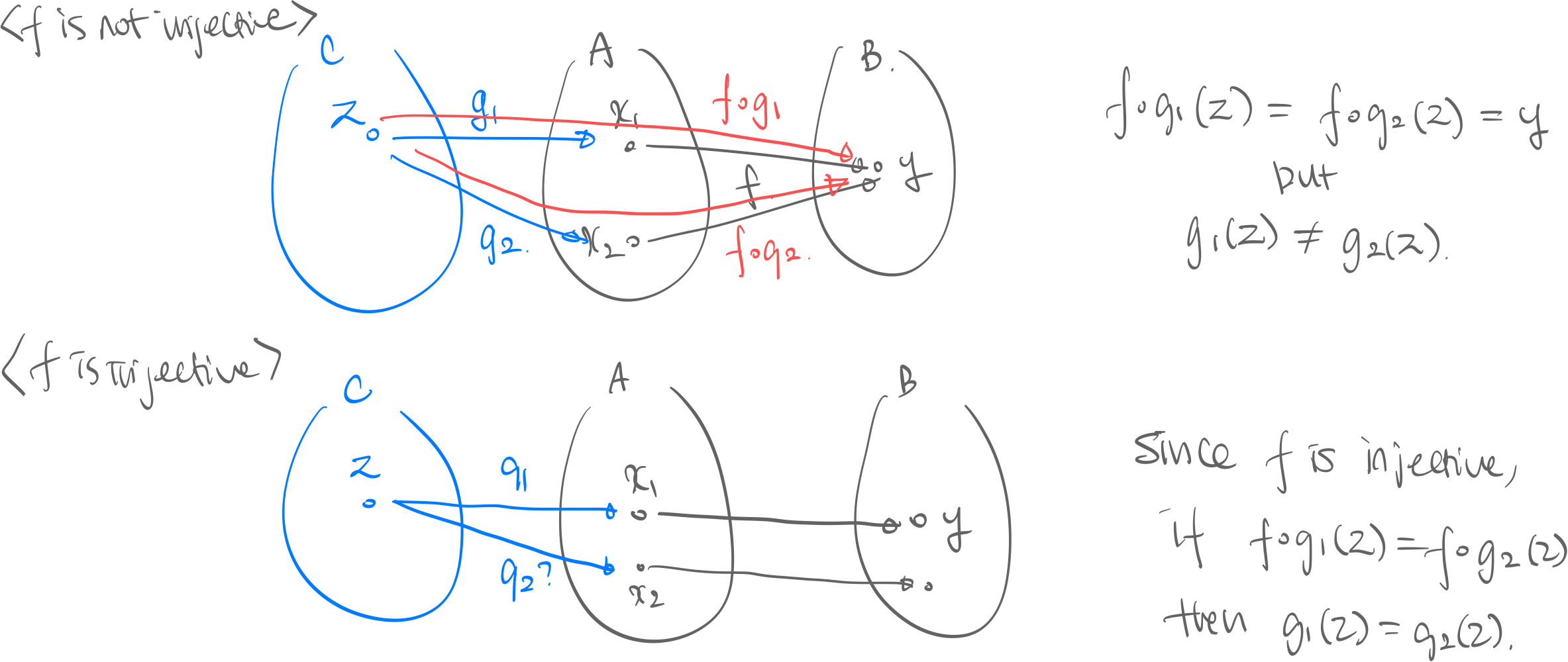
thm. In category $\text{Set}$ epimorphism is equivalent to $f$ being surjective, and monomorphism is equivalent to $f$ being injective.¹

• ! if function $f$ is surjective and injective, it’s invertible. But if morphism $f$ is epic and mono, it doesn’t mean it’s invertible. → Inverse of morphism may not exist if you don’t draw an arrow in between.

These definitions seems contrived, but you are assured they are for good reason¹

Footnotes §

1. morphism - Definition of Epimorphism in Category Theory - Mathematics Stack Exchange ↩ ↩²