Auto-Regressive & Moving Average

Autoregressive §

Motivation. You want to predict a time series, e.g. milk consumption per month. It is the most natural to say “future value is a weighted sum of past (realized) values.” The autoregressive model formalizes that. def. Autoregressive Process of order $p$. ($AR(p)$). $\{X_t\}$ is an $AR(p)$ process if it is modeled

$$X_t=\underset{\text{known at }{\mathcal{F}}_{t-1}}{\underbrace{{\varphi }_1{X}_{t-1}+{\varphi }_2{X}_{t-2}+\cdots +{\varphi }_p{X}_{t-p}}}+\underset{\text{ unknown }}{\underbrace{{ϵ}_t}}$$

where $\{{ϵ}_t\}\sim \text{WN}(0,{\sigma }_{ϵ}^2)$ which is called “innovation,” the “new” factor or information. Intution. Current value is the weighted sum of past $p$ values, plus some new thing that happened this time.

Moving Average §

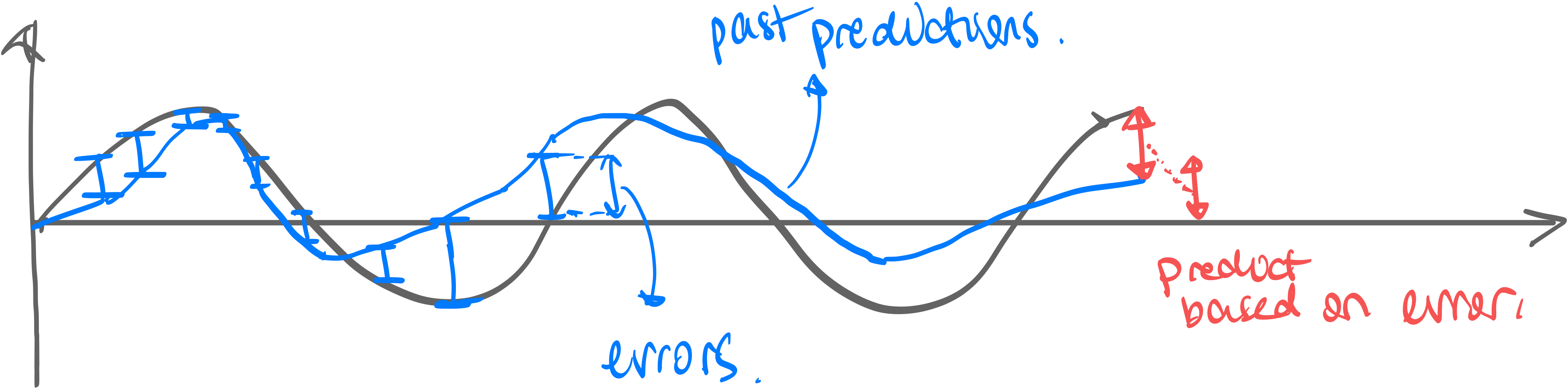
Motivation. But you might consider a more intelligent model, which is able to look back at the prediction errors in past data to predict current data. def. Moving Average Process of order $q$. $\{X_t\}$ is a $MA(q)$ process if it is modeled:

$$X_t=\underset{\text{known at }{\mathcal{F}}_{t-1}}{\underbrace{{\theta }_1{ϵ}_{t-1}+{\theta }_2{ϵ}_{t-2}+\cdots +{\theta }_q{ϵ}_{t-q}+}}+\underset{\text{ unknown }}{\underbrace{{ϵ}_t}}$$

where $\{{ϵ}_t\}\sim \text{WN}(0,{\sigma }_{ϵ}^2)$. We can also get its theoretical ACF as:

$$\rho (h)=\{\begin{array}{ll}\frac{{\sum }_{i=0}^{q-|h|}{\theta }_i\cdot {\theta }_{i+|h|}}{{\sum }_{i=0}^q{\theta }_i^2}& -q\le h\le q\\ 0& \text{else}\end{array}$$

Intuition. Current value is the weighted sum of past $q$ innovations and nothing else.

ARMA §

Now for the kicker: def. Autoregressive Moving Average process of order $p,q$. $\{X_t\}$ is an $\text{ARMA}(p,q)$ process if it is modeled:

$$X_t=\underset{\text{ learn from past data }}{\underbrace{\sum _{i=1}^p{\varphi }_i{X}_{t-i}}}+\underset{\text{ learn from past err }}{\underbrace{\sum _{i=1}^q{\theta }_i{ϵ}_{t-i}}}+\underset{\text{ only new info }}{\underbrace{{ϵ}_i}}$$

Invertibility, Causality §

thm. ARMA causality/invertibility condition. let $\text{ARMA}(p,q)$ process as above, and let:

$$\begin{array}{rl}\tilde{\varphi }(z)& =1-{\varphi }_{1}z-\cdots -{\varphi }_p{z}^p\\ \tilde{\theta }(z)& =1+{\theta }_{1}z+\cdots +{\theta }_q{z}^q\end{array}$$

now, if:

1. $\tilde{\varphi }(z),\tilde{\theta }(z)$ has no common roots
2. $\tilde{\varphi }(z)$ has roots $z$ outside the unit complex circle i.e. $|z|>1$ → Causality
3. $\tilde{\theta }(z)$ has roots $z$ outside the unit complex circle i.e. $|z|>1$ → Invertibility If causal, this process is causal with coefficients obtained from the following:

$$\sum _{i=0}^{\infty }{\psi }_i{z}^i=\frac{\tilde{\theta }(z)}{\tilde{\psi }(z)}$$

Example. $\text{ARMA}(1,1)$ has form $X_t={\varphi }_1{X}_{t-1}+{\theta }_1{ϵ}_{t-1}+ϵ$, with $|{\varphi }_1|<1$, and complex polynomials:

$$\begin{array}{rl}\tilde{\varphi }(z)& =1-{\varphi }_{1}z\\ \tilde{\theta }(z)& =1+{\theta }_{1}z\end{array}$$

And $z=\frac{1}{{\varphi }_1}$, $|{\varphi }_1|<1$ so we have a causal form. The coefficients obtained by:

$$\begin{array}{rlr}\sum _{i=0}^{\infty }{\psi }_i{z}^i& =\frac{1+{\theta }_{1}z}{1-{\varphi }_{1}z}=(1+{\theta }_{1}z)(1+{\varphi }_{1}z+{\varphi }_1^2{z}^2+\cdots )& \text{Geo. Sum expand}\\ & =(1+{\theta }_{1}z)\sum _{j=0}^{\infty }{\varphi }_1^j{z}^j& \\ & =\sum _{j=0}^{\infty }{\varphi }_1^j{z}^j+{\theta }_1\sum _{j=0}^{\infty }{\varphi }_1^j{z}^{j+1}\text{ }& \\ & =1+\sum _{i=1}^{\infty }({\varphi }_1^i+{\theta }_1{\varphi }_1^{i-1})z^i& \text{index start, from 0 to 1}\\ & =\underset{{\psi }_0}{\underbrace{1}}+\sum _{i=1}^{\infty }\underset{{\psi }_1,{\psi }_2,\dots }{\underbrace{{\varphi }_1^{i-1}({\varphi }_1+{\theta }_1)}}{z}^i.& \end{array}$$

Thus the causal form is:

$$X_t={ϵ}_t\cdot 1+\sum _{i=1}^{\infty }{\varphi }_1^{i-1}({\varphi }_1+{\theta }_1){ϵ}_{t-i}$$

ARIMA §

Motivation. Problem is when there is “drift” (=data generally moves up). This is corrected by using not the time series itself, but the “difference series” of that time series. def. Difference Operator. For process $\{X_t{\}}_{t\in \mathbb{N}}$ the difference operator $\nabla$ is defined as:

$$\begin{array}{rl}\nabla X_t& =X_t-X_{t-1}\\ {\nabla }^d{X}_t& =\{\begin{array}{ll}\nabla X_t& \text{if }d=1\\ {\nabla }^{d-1}(X_t-X_{t-1})& \text{if }d>1\end{array}\end{array}$$

• this has nothing to do with the gradient operator in calculus $\nabla$ Now we can define: def. Autoregressive Integrated Moving Average (ARIMA).

1. We have some series $\{X_t{\}}_{t\in \mathbb{N}}$ that keeps on drifting
2. Sowe difference it $d$ times, $Y_t={\nabla }^d{X}_t$ and got a new time seiries $\{Y_t\}$
3. $\{Y_t\}$ can be modeled as a $\text{ARMA}(p,q)$ time series.
4. Then, $\{X_t\}$ is a $\text{ARIMA}(p,d,q)$ time series Example. Let price of security $\{S_t\}$, and log-prices $\{\ln S_t\}$. Then obviously the log-returns $\left\{\ln S_t-\ln S_{t-1}=\ln \frac{S_t}{S_{t-1}}\right\}$ is the difference series ${\nabla }^1\ln S_t$. If the log-returns series can be modeled as an $\text{ARMA}(p,q)$ then the original log-prices is an $\text{ARIMA}(p,1,q)$ model.